Параметры состояния термодинамической системы

1. Давление , здесь dF_n – элемента силы давления, действующая перепендикулярно площади. Площадь dS.

С точки зрения МКТ – давление есть результат взаимодействия атомов и молекулов со стороны сосуда.

2. Температура – в наших ощущениях Т воспринимается, как мера нагретости тела, есть привести в соприкосновении более наргетое тело с менее награтым телам, то через некоторое время их нагретости станут одинаковыми, при этом мы говорим, что температуры тел выровнялись, при этом мы говорим, что от более наргетого тела к менее нагретому прямо тепло.

С точки зрения МКТ температура мера средней кинетической энергии поступательно двух малекул.

3. Объем – простанство, ограниченное границами, для данноц массы газа, чем обльше объемы , тем больще среднее расстояние между молекулами.

Равновесное состояние – такое состяние изалированное системы, в которой она в конце концов самопроизвольно приходит и остается в этом состоянии бесконечно долго, при этом во всех тогках система Т и р окащываются одиноковыми.

Газ, полностью подчиняющимся этому уравнению называется идеальный газ.

Идеальным называется газ, взаимодействия между молекулами у которого можно пренебречь

Процесс называется равновесными, если от проходит через непрерывную последовательность равновесных состояний.

3 формы записи уравнения состояния идеального газа:

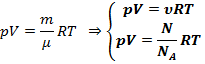
N - число молекул в единицу объема

Рассчитаем объем занимаемый газом при натураном условии Т = 273,15К, р = 1,01.10⁵ Па

Термодинамический процесс – процесс перехода вещества изодного состояния в дргуое состояние, а возможен за счет сильного воздействия или за счет теплообмена в виде теплоты с окруность средой.

18. Плотность идеального газа. Связь между давлением, концентрацией и температурой. Изопроцсесы в идеальном газе.

Плотность идеального газа

Связь между давлением, концентрацией и температурой

Изопроцессы – такие, в которых один из параметров поддерживается постоянными, а второй параметр является функцией третьего параметры.

1. Изотермический процесс T = const (m=const)

2. Изобаный процесс р = const (m = const)

3. Изохорный процесс V = const (m=const)

19. Основное уравнение молекулярно - кинетической теории (связь между давлением и средней кинетической энергией поступательного движения молекул газа). Связь между средней кинетической энергией поступательного движения молекулы и температурой.

Рассмотрим взаимодействия между газом со стенкой сосуды, в которой газ находится.

Основные условия:

1. Газ одноатомный

2. Газ разрежен, поэтому среднее растояние между молекулами высокие, то есть силы взаимодействия между молекулами мало, то можно рассмотрить действия друг с другом.

3. Размеры молекул пренебречь.

4. Рассмотриваем молекулы как упругие, которой обсолютно друга со стенкой сосуды.

Пусть имеем масса одной молекулы m_o. Нормаль

Пусть : время взаимодействия одной молекулы со стенкой, тогда повторим закон Ньютона

Рассмотрим действия молекул на стенку площадью S, находящиеся молекулы

Числа ударов молекул от стенки равняестя

Где n: концентрация молекул в сосуде

V: объем сосуды

Где: l равняется длину, через который один молекула скоростью проходил за время

так как стенки только движуются половину молекул и с коростью v­_x,

Тогда суммарный импульс сил действующих на стенку за время t будет равняется.

Здезь F: суммарные силы давления, действрующие на стенку за время t

Так как скорость разные между молекулами, то есть должны говорить от среднего квадратного .

Силы входяющией молекул может оденоковы.

Тогда сила давления:

По определению

Средняя кинетическая энергия одной молекулы

20. Физический смысл температуры. Средняя квадратичная скорость молекулы газа.

Температура – в наших ощущениях Т воспринимается, как мера нагретости тела, есть привести в соприкосновении более наргетое тело с менее награтым телам, то через некоторое время их нагретости станут одинаковыми, при этом мы говорим, что температуры тел выровнялись, при этом мы говорим, что от более наргетого тела к менее нагретому прямо тепло.

С точки зрения МКТ температура мера средней кинетической энергии поступательно двух малекул.

А вообщее на двух или трех атомный молекулы, скажет что температура есть мера средней кинетичекой энергии поступательного движения одной молекулы.

Средная кинетическая квадратичная скорость называется: