32. Проверка гипотезы о числовом значении дисперсии признака в генеральной совокупности.

1. Задается уровень значимости критерия, как правило в условии задач: ( α=0,01, 0,02, 0,05, 0,1, 0,005)

2.

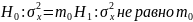
3.

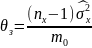
4.

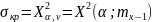
5. Проверяется соотношение

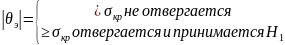
33.Проверка гипотезы о числовом знач доли признака в гс.

П усть имеется выборка Х1…Хn в соответствии N признака Х, и пусть требуется проверить гипотезу о том, что доля признака ГС= предполагаемому значению Rо 1. Вызов.гипотезу Ho:Р=Ro p=Ro где Р-доля пр-ка в ГС. 2.Ні= p<Ro Ro-предполаг. значение

p>Ro доли признака в ГС

3.Экпер. значение стат-ки определяется формулой 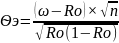,где .

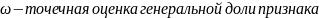4 . Ф(Ѳкр)=1-α= Н1:Р≠Ro

Ѳ э= Ф(Ѳкр)=1-2α Н1:Р>Ro p<Ro Tα,v=Тα,n-1 Н1: Р≠Ro Tα,v=Tα,n-1 h1: Р>Ro p<Ro

5 . = ≤Ѳкр Но: Н/отверг. >Ѳкр Но: отверг. И прин. Н1

3 4. Проверка гипотезы о равенстве средних значений двух нормальных ГС. Пусть из 2 ГС V-ми №1 и №2 извлечены 2 выборки n1 и n2 знач. Х1….Хn1=Y1….Yn2 норм. Распред. Признака Х в I ГС, Y во II ГС. проверим гипотезу о том, что ген.ср=между собой 1. Но=Х=Y, Н1: Х≠Y

X>Y гдеХ и Y – ср.знач.призн.Хи Yв ГС.

X<Y 2. Задано таблицей 3. Экспер.знач.стат-ки крит.

Ѳ э= 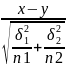в случае, если дисперсии известны И=соответственно

и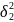

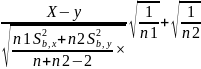в случае если дисперсии Гс не известны

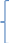
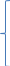
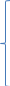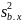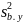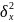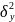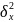3 5. Проверка гипотезы о равенстве дисперсий двух нормал ГС. пусть из 2 ГС V-ами №1 и №2 извлечены выборки n1 и n2 нормально распределенных в ГС. Пусть по данным найдены выб-е значения дисперсий и . проверим гипотезу о равенстве дисперсий: 1. Но: = , Н1: ≠ > < 2. Ѳэ= 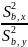, если > 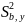, если < 3. Ѳкр= > <

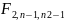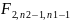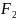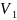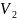, , - квинтиль Фишера-Снедекора, в таблице приложения.

36. Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона.

37. Проверка гипотезы о показательном распределении генеральной совокупности с помощью критерия Пирсона.

38. Проверка гипотезы о равномерном распределении генеральной совокупности с помощью критерия Пирсона.

Проверка гипотезы о нормальном распределении признака в ГС

Схема проверки:

1^о. Выдвигается гипотеза Но: признак Х в ГС распределён по нормальному закону, и альтернативная гипотеза Н1: признак в ГС распределён по другому, отличному от нормального, закону распределения.

2^о. Вычисляются теоретические вероятности

p_i’ = P(x_i ≤ X ≤ x_i+1)=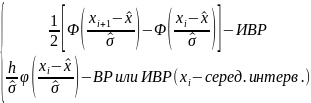

• Φ(х) – ненормальная функция Лапласа.

• φ(х) – малая функция Лапласа, значение даны в приложениях учебника.

• h – разница между двумя соседними вариантам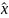и.

• и 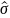- несмещённые точечные оценки генерального среднего и генерального сред. квадратич. отклонения, опред. равенством: ; .

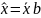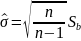3^o. Вычисляются теоретические частоты по формуле: n_i’ = p_i’ n

4^o. Находится экспериментальное значение статистики критерия по формуле

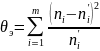, где

• m – число вариант (интервалов).

• n_i – эксперемент. частоты, заданные в ВР или ИВР

5^о. Находится при заданном уровне значимости α критическое значение статистики критерия 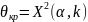, где

• k – число степеней свободы распределения: .

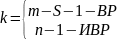• S – число параметров проверяемого закона распределения (при S = 2).

6^o. Сравнивается эксперемент. и критическ. значения статистики и делается соответствующий статистический вывод:

.

Примечания:

1^о. По аналогичной схеме провер. гипотеза о распределении признака в ГС по другим законам, находясь при этом, теоретические частоты 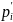соответствуют формулам проверяемого закона: =

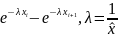• при проверке распред. признака в ГС по показательному закону

• – по равномерному закону

• – по биномиальному закону

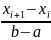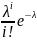• – по закону Пуассона

2^о. При проверке распред. признаков в ГС по нормальному закону интервалы с частотами, меньшими 5 объединяются с соседними.

3^о. Критерий является приближённым и применим при объёмах выборки ≥30, а лучше ≥50.