
- •1.Предмет и задачи теории вероятностей. Пространство элементарных событий.
- •2. Случайные события и их классификация. Операции над событиями.
- •3 Частота появления случайного события и ее свойства.
- •4. Вероятность случайного события и её свойства
- •5.Статистическое, классическое, аксиоматическое и геометрическое опред вероятности случайного события.
- •6. Теоремы сложения вероятностей событий.
- •7.Теоремы умножения вероятностей событий. Условная вероятность. Независимость событий.
- •9.Схема испытаний Бернулли. Формула Бернулли. Производящая функция. Наивероятнейшее число наступления события.
- •10.Теоремы Муавра-Лапласа и Пуассона и их применение в схеме испытаний Бернулли.
- •11. Формула полной вероятности. Формула Байеса.
- •12. Определение случайной величины. Классификация случайных величин. Закон распределения случайной величины. Формы задания закона распределения дискретной св
- •13. Функция распределения и ее свойства.
- •14.Плотность вероятности случ величины и ее св-ва.
- •16. Биноминальное распределен и его числ. Хар-ки
- •18.Равномерное распределение и его числовые характеристики.
- •19. Показательное распределение и его числовые характеристики.
- •20. Нормальный закон распределения и его числовые характеристики. Функция Лапласа.
- •22.Теоремы Чебышева, Бернулли и Пуассона.
- •23. Центральная предельная теорема теории вероятностей и ее следствие.
- •24. Предмет и задачи мат. Статистики. Ген. И выборочная сов-ти. Формы записи исходных статистич. Данных. Статистический, вариационный и интервальный ряды и их хар-ки.
- •25.Графическое представление распределений.
- •26. Понятие оценки. Виды оценок. Свойства оценок. Точечные оценки параметров ген. Совокупности и методы их получения
- •27.Понятие интервальной оценки. Доверительный интервал и доверительная вероятность. Доверительный интервал для генеральной средней нормально распределенной сов-ти.
- •30. Критерии проверки параметрических и непараметрических гипотез: t-критерий, f –критерий, критерий согласия Пирсона, критерий согласия Колмогорова (самостоятельно).
- •32. Проверка гипотезы о числовом значении дисперсии признака в генеральной совокупности.
- •33.Проверка гипотезы о числовом знач доли признака в гс.
- •36. Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона.
- •37. Проверка гипотезы о показательном распределении генеральной совокупности с помощью критерия Пирсона.
- •38. Проверка гипотезы о равномерном распределении генеральной совокупности с помощью критерия Пирсона.
- •39.Проверка гипотезы о равномерном распределении генеральной совокупности с помощью критерия Колмогорова
- •40. Проверка гипотезы о распределении генеральной сов-ти по биномиальному закону с помощью критерия Пирсона.
- •41. Проверка гипотезы о распределении ген. Сов-ти по з-ну Пуассона с помощью критерия Пирсона.
- •42.Основные понятия дисперсионного анализа. Проверка гипотезы о равенстве генеральных групповых дисперсий. Критерий Бартлетта.
- •43.Проверка гипотезы о значимости влияния фактора на результативный признак с помощью дисперс анализа.
- •44. Проверка гипотезы о равенстве групповых средних с помощью дисперсионного анализа.
- •46.Выборочный парный коэффициент линейной корреляции, его свойства и значимость. Коэффициент детерминации, его свойства и интерпретация.
- •47.Выборочный множественный коэффициент корреляции, его свойства и значимость
- •48.Выборочные частный коэффициенты корреляции, их свойства и значимость. Матрица парных коэффициентов корреляции.
- •15. Основные и не основные числовые характеристики случайной величины, их свойства и способы их вычисления. (зр и чх св)
- •49. Понятие регрессии. Задачи регресс анализа. Модель регрессии. Линейная парная регрессия. Метод наим квадратов опред параметров линейного уравнения регрессии.
- •45 Понятие о линейной корреляции и регрессии. Представление данных в корреляционном анализе.
18.Равномерное распределение и его числовые характеристики.
Опр: НСВ х наз-ся распред по равномерному закону на отр. АВ с параметрами а и b, если ее плотность распред вероятностей равна постоянной вел-не на этом отрезке и равна нулю вне этого отрезка:
f(x)=

Найдем постоянную с использ. условия нормировки;
с-
?
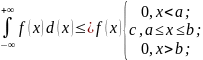

f(x)
=
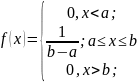 ;
;
Ф-я
распределения равномерной СВ Х имеет
вид F(x)
=
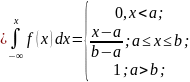
График функций распред и плотности имеют вид
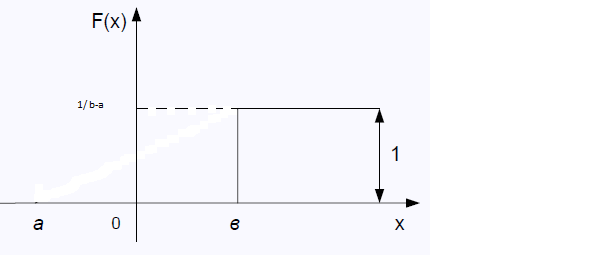
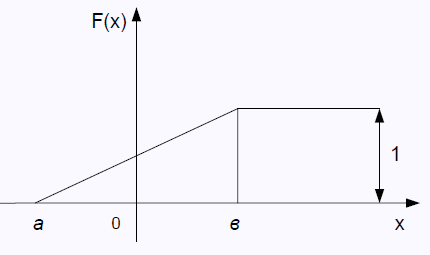
Числовые хар-ки равномерного распределения опред. равенствами
m(x)
=
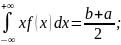
D=
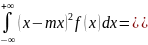
Вероятность попадания равномерной случ. величины в интервал α, b € [a, b]
опред
выражением P
( x
€ ( α,
b)
€[ a,b]
= P
( a<x<b)
=
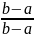 причем знаки
неравенств могут быть и не строгими;
причем знаки
неравенств могут быть и не строгими;
Примечание: Равномерное распределение не имеет моды, а его медиана и мат. ожидание равны между собой;
19. Показательное распределение и его числовые характеристики.
Н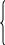 епрерывная
CВ X называется
распределительной по показательному
закону с параметром λ >
0, если её плотность распределения вероятностей
определяется формулой:
епрерывная
CВ X называется
распределительной по показательному
закону с параметром λ >
0, если её плотность распределения вероятностей
определяется формулой:
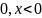
f(x)=
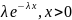
График плотности показательного распределения:

f(x)


x

F(x)=
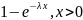
Основные числовые хар-ки показателей определяются формулами:
mx=
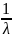
Dx=
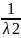 => λ=
=> λ=
σx=
20. Нормальный закон распределения и его числовые характеристики. Функция Лапласа.
Непрерывной СВ X наз. Распределённая по нормальному закону (по закону Гаусса) с параметрами mx и σx , если её плотность распр-я вероятностей определяется выражением:
f(x)=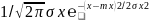
Фун-ция распределения определяется:
F(x)=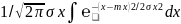
Г
 рафик
плотности распределения наз. нормальной
кривой/кривой Гаусса и имеет вид:
рафик
плотности распределения наз. нормальной
кривой/кривой Гаусса и имеет вид:


Вероятность попадания СВ в интервал (α,β):
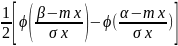
где
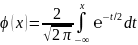 - ф-я
Лапласса
- ф-я
Лапласса
Следствие:
P(|x-
mx|<ε)= )
)
21.Неравенства
Маркова и Чебышева и различные формы
их записи.
Формулировка
нер-ва Маркова Если
среди зн СВ Х нет отриц, то вер-ть того,
что она примет какое-н зн, превосходящее
полож число А,
не больше дроби 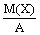 ,
т.е.
,
т.е.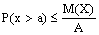 , а
вер-ть того, что она примет какое-н зн,
не превосходящее полож числа А,
не меньше
, а
вер-ть того, что она примет какое-н зн,
не превосходящее полож числа А,
не меньше  ,
т.е.
,
т.е.
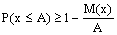 1ая
форма нер-ва Чебыш Вер-ть
того, что отклонение СВ Х от ее
матеможидания, а произойдет по абсолютной
величине постоянное число Е>0, не
больше
1ая
форма нер-ва Чебыш Вер-ть
того, что отклонение СВ Х от ее
матеможидания, а произойдет по абсолютной
величине постоянное число Е>0, не
больше 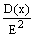 ,
т.е.
,
т.е.
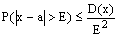 2ая
форма нер-ва Чебыш Вер-сть
того, что отклонение СВ Х от ее
матеможидания, а не произойдет по
абсолютной величине постоянного числа
Е>0, не меньше
2ая
форма нер-ва Чебыш Вер-сть
того, что отклонение СВ Х от ее
матеможидания, а не произойдет по
абсолютной величине постоянного числа
Е>0, не меньше 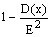 ,
т.е.
,
т.е.
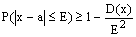 Говорят,что
послед-сть СВ
Говорят,что
послед-сть СВ 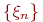 сходится
по вер-ти к Св
сходится
по вер-ти к Св ![]() при
при ![]() ,
и пишут
,
и пишут 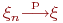 ,
если для люб
,
если для люб ![]()
![]()
22.Теоремы Чебышева, Бернулли и Пуассона.
Теорема Чебышева:
Если
свободный член X1……Xn
попарно независимы, имеют
равномерно-ограниченные дисперсии
P(X1)=C…..P(Xn)=C
и одинаковые вероятности M(X1)=…=M(Xn),
то среднее арифметическое данных величин
сходятся по вероятности и их мат.
ожидания.
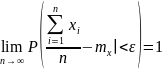 ,
где mx=M(X1)….M(Xn)
,
где mx=M(X1)….M(Xn)
Доказательство:
1.Рассмотрим
CВ
Ч является средним арифметическим
значением X=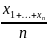 задан. CВ
и найдём для неё мат.ожидание
задан. CВ
и найдём для неё мат.ожидание

2.Воспользуемся неравенством Чебышева.
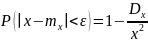 => прим. его для
суммы СВ:
=> прим. его для
суммы СВ:
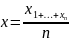 ;
имеем
;
имеем
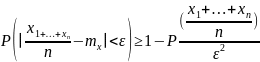 =˃используя
свойства дисперсии получим:
=˃используя
свойства дисперсии получим:
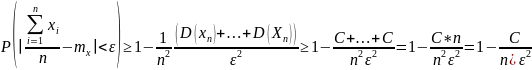 ;
переходим в
последнем неравенстве к пределу при
n→∞:
;
переходим в
последнем неравенстве к пределу при
n→∞: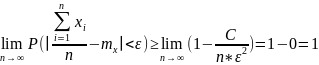 и т.д.
и т.д.
Обобщённая теория Чебышева:
Если попарно независимые и одинаково распределённые величины x1…x2, имеют ограниченные одним и тем же числом дисперсии D(x1)=C,…,D(xn)≤C и конечные не равные между собой математические ожидания H(x1)≠…≠H(xn), то среднее арифметическое данных CВ сходится на вероятности к среднему арифметическому их мат.ожидания:

Доказательство аналогично пред идущему.
Теорема Бернулли:
Если в каждом из n независимых испытаний вероятность появления некоторых событий А, если постоянная величина равна Р в каждом из n испытаний, то при достаточно большом числе испытаний , часто появления данного события сходится к вероятности его появления по условию сходимости по вероятности:

m-число появлений события А в n испатаниях.
