9.Схема испытаний Бернулли. Формула Бернулли. Производящая функция. Наивероятнейшее число наступления события.
Формула Бернулли. Пусть в одинаковых условиях проводится n независимых испытаний, в каждом из которых событие А произойдёт, то испытание – успешное, а само событие – успех.
Если испытание повторяется n раз с соблюдением условий:
Вероятность успеха в каждом испытании одна и та же.
Результат любого испытания не зависит от исходов предыдущих испытаний, то такая последовательность испытаний с двумя исходами успех, неудача называется послед. независ. испытаний Бернулли и схемой Бернулли.
Теорема Бернулли. Если в одинаковых условиях проводится n независимых испытаний, в каждом из которых вер-ть появления события А постоянна
и = р(Р(А)= р) , а вер-ть ненаступления = q (q=1-p), то вер-ть того, что в n-испытаниях событие А появится ровно n раз определяется формулой:
Р(А)= Рm,n=Cnm pmqn-m
и называется формулой Бернулли.
Число,к кот. при заданном числе испытаний, соотв. максимальная вер-ть событий, называется наивероятнейшим числом наступления данного события и обозначается m0.
В схеме испытаний Бернулли наивероятнейшее число наступления события определяется формулой: np-q≤m0≤np+p
10.Теоремы Муавра-Лапласа и Пуассона и их применение в схеме испытаний Бернулли.
Пусть приводится n независимых испытаний в одинак. условиях, в каждом из которых событие A может появиться с одной и той же вероятностью p=P(A) или может, не появится с вероятностью q=1-q. При достаточно большом n ,с целью избегания громоздкости вычислений, при вычислении вероятностей наступления события A ровно m раз или от m1 до m2 раз по формуле Бернулли пользуются приближенными формулами Лапласа и Пуассона.
Локальная теорема Лапласа:
Если проводится
достаточно большое число испытаний n
(n→∞)
в одинаковых условиях в каждом из которых
вероятность появления события A
постоянно равно p
и не очень близка к нулю и единице,
вероятность наступления события A
в n
испытаний
ровно m
раз определяется формулой
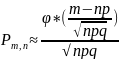называемой локальной формулой Лапласа
в которой
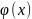есть малая функция Лапласа определяется
формулой
;
;
;
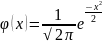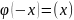значения
которой затабулированны и даны в
дополнениях учебников.
Интегральная теорема Лапласа:
Если в одинаковых условиях проводится достаточно большое число независимых испытаний n (n→∞), в каждом из которых вероятность наступления события А постоянно равно p и не очень близка к нулю и единице, то вероятность того, что в n испытаниях события А наступит от m1 до m2 раз, определяется приближенной интегральной формулой Лапласа:
,
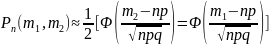в которой Φ(х)-функция Лапласа (не
нормированная) определяемая равенством:
;
значения которой затабулированны.
11. Формула полной вероятности. Формула Байеса.
Пусть проводится некоторый опыт. Об условиях проведения, которого можно сделать n взаимоисключающих друг друга предположений (гипотез) Н1 … Hn, составляющих полную группу событий. И пусть событие А может произойти только вместе с одной из этих гипотез, т.е. событие А можно представить как сумму n несовместимых событий.
А = АН1 +АН2 +…+АНn (откуда по примеру сложения вероятностей соб. След.) Р(А) = Р(АНx + …+ Р(АНn)) = P (∑ni=1 AHi)= Р((∑ni=1 HiA) = ∑ni=1 Р (HiA) (откуда использую теорему умножения)
Р(НiА)=Р(Нi) × P(A/Hi) получаем:
P(A) = ∑ni=1 P(Hi) × P(A/Hi) – формула полной вероятности вычисления вероятности события, где P(Hi) – вероятность i-ой гипотезы, Р (A/Hi) – условная вероятность события А при данной гипотезе. Распишем по т. Умножения вероятность события: P(AHi) = P(HiA) = P(Hi) × P(A/Hi) = P(A) × P(Hi/A) → P(Hi/A) = P(Hi) × P(A/Hi) / P(A), где Р(А) – полная вер-сть события А опред. Ф-ой 1.
Р(Hi/A) – условная вероятность i-ой гипотезы (вероятность i-ой гипотезы после проведения опыта). Формула 2 называется формулой Байеса.
Доопытные (первоначальные) вероятности гипотез P(Hi) наз. Априортными, а послеопытные P(Hi/A) - апостериортными.