30. Критерии проверки параметрических и непараметрических гипотез: t-критерий, f –критерий, критерий согласия Пирсона, критерий согласия Колмогорова (самостоятельно).

Пусть даны выборка  X = ( ) из неизвестного совместного распределения  , и семейство статистических гипотез  . Тогда статистическим критерием называется функция, устанавливающая соответствие между наблюдаемыми величинами и возможными гипотезами: f : .

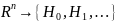Таким образом каждой реализации выборки   статистический критерий сопоставляет наиболее подходящую с точки зрения этого критерия гипотезу о распределении, породившем данную реализацию.

Критерий Пирсона Обозначим через X исследуемую случайную величину. Пусть требуется проверить гипотезу H₀ о том, что эта случайная величина подчиняется закону распределения F(x). Для проверки гипотезы произведём выборку, состоящую из n независимых наблюдений над случайной величиной X. По выборке можно построить эмпирическое распределение F ^* (x) исследуемой случайной величины. Сравнение эмпирического распределения F ^* (x) и теоретического (или, точнее было бы сказать, гипотетического - т.е. соответствующего гипотезе H₀) распределенияF(x) производится с помощью специального правила — критерия согласия. Одним из таких критериев и является критерий Пирсона. Для проверки критерия вводится статистика:

;

где 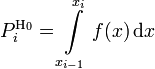  — предполагаемая вероятность попадения в i-й интервал,   — соответствующее эмпирическое значение, n_i — число элементов выборки из i-го интервала, N — полный объём выборки. Также используется расчет критерия по частоте, тогда:

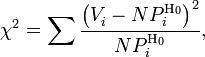
где V_i - частота попадания значений в интервал. Эта величина в свою очередь является случайной (в силу случайности X) и должна подчиняться распределению χ².

 критерий согласия Колмогорова

Обозначим нулевую гипотезу  , как гипотезу о том, что выборка подчиняется распределению  . Тогда по теореме Колмогорова для введённой статистики справедливо:

Учтём, что критерий имеет правостороннюю критическую область.

Если α достаточно близко к 1, то   можно приблизительно рассчитать по формуле:

Асимптотическая мощность критерия равна 1

3 1. Проверка гипотезы о численной величине среднего значения признака в ГС. Пусть признак Х распределен нормально в ГС объема N. И пусть х1….хn выборочное значение признака Х из данной ГС. Предположим Х=Mo и проверим данное предположение: 1. Но:х=Мо, Мо-предполагаемое значение генерального среднего. Х-генеральное среднее. 2. Мі: Х≠Мо Х<Мо

Х>Мо

3. Экспериментальное значение в стат-ке определяется формулой: , если ГС известна 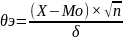, если дисперсия ГС не известна 4. Критическое значение статистически определяется ср.

кр= Ф(Ѳкр)= =1-α

Ф(Ѳкр)=1-2α если дисперсия ГС известна и =

T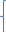 α,о=Тα,n-1 – М1:Х≠Мо Тα,о=Тα,n-1 – М1: Х>Мо

X<Мо если дисперсия ГС неизвестна

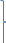5. <Ѳкр. – М1:х≠Мо Но не отвергается

Ѳэ= Ѳэ<Ѳкр – М1:Х>Mo если Но отверг.,то

Ѳэ>-Ѳкр – М1:Х<Мо принимает Н1

Примечание: В случае больших объемов выборок Ѳкр находится аналогично случаю, когда известна дисперсия ГС.