
- •1.Предмет и задачи теории вероятностей. Пространство элементарных событий.
- •2. Случайные события и их классификация. Операции над событиями.
- •3 Частота появления случайного события и ее свойства.
- •4. Вероятность случайного события и её свойства
- •5.Статистическое, классическое, аксиоматическое и геометрическое опред вероятности случайного события.
- •6. Теоремы сложения вероятностей событий.
- •7.Теоремы умножения вероятностей событий. Условная вероятность. Независимость событий.
- •9.Схема испытаний Бернулли. Формула Бернулли. Производящая функция. Наивероятнейшее число наступления события.
- •10.Теоремы Муавра-Лапласа и Пуассона и их применение в схеме испытаний Бернулли.
- •11. Формула полной вероятности. Формула Байеса.
- •12. Определение случайной величины. Классификация случайных величин. Закон распределения случайной величины. Формы задания закона распределения дискретной св
- •13. Функция распределения и ее свойства.
- •14.Плотность вероятности случ величины и ее св-ва.
- •16. Биноминальное распределен и его числ. Хар-ки
- •18.Равномерное распределение и его числовые характеристики.
- •19. Показательное распределение и его числовые характеристики.
- •20. Нормальный закон распределения и его числовые характеристики. Функция Лапласа.
- •22.Теоремы Чебышева, Бернулли и Пуассона.
- •23. Центральная предельная теорема теории вероятностей и ее следствие.
- •24. Предмет и задачи мат. Статистики. Ген. И выборочная сов-ти. Формы записи исходных статистич. Данных. Статистический, вариационный и интервальный ряды и их хар-ки.
- •25.Графическое представление распределений.
- •26. Понятие оценки. Виды оценок. Свойства оценок. Точечные оценки параметров ген. Совокупности и методы их получения
- •27.Понятие интервальной оценки. Доверительный интервал и доверительная вероятность. Доверительный интервал для генеральной средней нормально распределенной сов-ти.
- •30. Критерии проверки параметрических и непараметрических гипотез: t-критерий, f –критерий, критерий согласия Пирсона, критерий согласия Колмогорова (самостоятельно).
- •32. Проверка гипотезы о числовом значении дисперсии признака в генеральной совокупности.
- •33.Проверка гипотезы о числовом знач доли признака в гс.
- •36. Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона.
- •37. Проверка гипотезы о показательном распределении генеральной совокупности с помощью критерия Пирсона.
- •38. Проверка гипотезы о равномерном распределении генеральной совокупности с помощью критерия Пирсона.
- •39.Проверка гипотезы о равномерном распределении генеральной совокупности с помощью критерия Колмогорова
- •40. Проверка гипотезы о распределении генеральной сов-ти по биномиальному закону с помощью критерия Пирсона.
- •41. Проверка гипотезы о распределении ген. Сов-ти по з-ну Пуассона с помощью критерия Пирсона.
- •42.Основные понятия дисперсионного анализа. Проверка гипотезы о равенстве генеральных групповых дисперсий. Критерий Бартлетта.
- •43.Проверка гипотезы о значимости влияния фактора на результативный признак с помощью дисперс анализа.
- •44. Проверка гипотезы о равенстве групповых средних с помощью дисперсионного анализа.
- •46.Выборочный парный коэффициент линейной корреляции, его свойства и значимость. Коэффициент детерминации, его свойства и интерпретация.
- •47.Выборочный множественный коэффициент корреляции, его свойства и значимость
- •48.Выборочные частный коэффициенты корреляции, их свойства и значимость. Матрица парных коэффициентов корреляции.
- •15. Основные и не основные числовые характеристики случайной величины, их свойства и способы их вычисления. (зр и чх св)
- •49. Понятие регрессии. Задачи регресс анализа. Модель регрессии. Линейная парная регрессия. Метод наим квадратов опред параметров линейного уравнения регрессии.
- •45 Понятие о линейной корреляции и регрессии. Представление данных в корреляционном анализе.
26. Понятие оценки. Виды оценок. Свойства оценок. Точечные оценки параметров ген. Совокупности и методы их получения
Параметрами распределения или описательными статистическими признаками ГС назыв. Числовые характеристики данного признака, описывающие его распределение ГС.
1.Рассмотрим
признак Х ГС, распределённый по какому-то
конкретному закону, и пусть
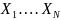 его значения ГС. Выберем случайным
образом n
из ГС. Предположим, что данное выборочное
значение представлено в виде вариационного
или интервального вариационного
распределения и необходимы выборочное
значение дисперсии, среднее квадратичное
отклонение. Требуется по данным числовым
характеристикам оценить параметры
распределения ГС сохранения всех
вероятностных свойств.
его значения ГС. Выберем случайным
образом n
из ГС. Предположим, что данное выборочное
значение представлено в виде вариационного
или интервального вариационного
распределения и необходимы выборочное
значение дисперсии, среднее квадратичное
отклонение. Требуется по данным числовым
характеристикам оценить параметры
распределения ГС сохранения всех
вероятностных свойств.
2.
Функция, зависящая от экспериментальных
данных и построение по отрицательному
правилу называется статичной, а её
значение называется оценкой и обозначается
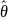 .
.
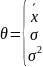
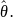
3.
Точечной оценкой параметра распределения
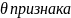 Х
ГС называется оценка
,
определяемая одним числом по опред.
правилу из выборочных данных данного
признака.
Х
ГС называется оценка
,
определяемая одним числом по опред.
правилу из выборочных данных данного
признака.
4. Пусть из ГС значения признак Х извлечена случайным образом выборочная совокупность,
1)для
среднего
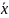 будет являться оценка
будет являться оценка
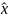 ,
определяемая равенством
,
определяемая равенством
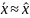 ,
,
2)
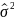 =
= ,
,
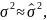 3)
3)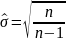
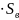 ,
,
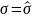 4)
4)
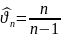
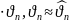 ,5)
,5) =
=
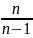
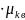 ,
,
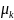 =
=
27.Понятие интервальной оценки. Доверительный интервал и доверительная вероятность. Доверительный интервал для генеральной средней нормально распределенной сов-ти.
Опред.1 Доверительным интервалом (интервальной оценкой) для неизвестного параметра Ө ГС наз. интервал (Ө1, Ө2), содержащ. неизвестное значение данного параметра Ө с вероятностью ɣ: P(Ө1< Ө< Ө2) = ɣ.
Опред.2 Число гамма ɣ называется доверительной вероятностью или уравнением надежности, а число α = 1- ɣ называется уравнением значимости ɣ.
Опред.3 Статистики Ө1= Ө1 (х1, …, хn) и Ө2= Ө2 (х1, …, хn), определяемые по экспериментальным данным, называется нижней и верхней границами доверительного интервала.
При увеличении числа выборки n длина доверительного интервала уменьшается, а при приближении доверительной вероятности ɣ→1 – длина доверительного интервала увеличивается.
Опред.4 Предельной ошибкой выборки называется наибольшее значение отклонения точечной оценки параметра от его истинного значения.
Доверительный интервал для генерального среднего значения признака.
Пусть признак Х нормально распределен в ГС и пусть х1, …, хn – его выборочные значения. (X€N(mx, ᵟx). Предположим, что задана доверительная вероятность ɣ, тогда доверительный интервал для генерального среднего значения признака определяется формулой:

где
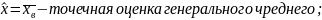
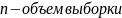
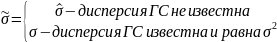
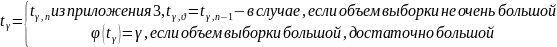
28.
Доверительный интервал для среднего
квадратичного отклонения.
Требуется найти доверительные интервалы,
покрывающие параметры Dи s с
заданной надежностью g.
Потребуем выполнения соотношения
![]() .
Раскроем модуль и получим двойное
неравенство:
.
Раскроем модуль и получим двойное
неравенство:
![]() .
Преобразуем:
.
Преобразуем:
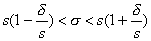 .
Обозначим d/s
= q (величина q находится
по "Таблице значений q"и зависит
от надежности и объема выборки),
тогда доверительный интервал для оценки
генерального среднего квадратического
отклонения имеет вид:
.
Обозначим d/s
= q (величина q находится
по "Таблице значений q"и зависит
от надежности и объема выборки),
тогда доверительный интервал для оценки
генерального среднего квадратического
отклонения имеет вид:
![]() .
Замечание : Так как s >0, то
если q >1
, левая граница интервала равна
0: 0< s < s (
1 + q ).
.
Замечание : Так как s >0, то
если q >1
, левая граница интервала равна
0: 0< s < s (
1 + q ).
29.Понятие
статистической гипотезы.
Под статистическими подразумеваются
такие гипотезы,
которые относятся или к виду, или к
отдельным параметрам распределения
случайной величины. Простая
гипотеза однозначно
характеризует параметр распределения
случайной величины. Сложная гипотеза
состоит из конечного или бесконечного
числа простых гипотез, здесь указывается
некоторая область вероятных значений
параметра. Нулевая
гипотеза (Но)
— это гипотеза о том, что есть две
совокупности, которые сравниваются по
одному или нескольким признакам, не
отличаются. Параметрическая
гипотеза — это гипотеза о параметрах
генеральной совокупности. Непараметрическая
гипотеза — это гипотеза о параметрах
распределения. Ошибка
первого рода состоит
в том, что будет отвергнута правильная
гипотеза. Ошибка
второго рода состоит
в том, что будет принята неправильная
гипотеза. статистический
критерий определяется
статистикой T и
критическим множеством 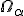 ,
которое зависит от уровня значимости
,
которое зависит от уровня значимости ![]() .
Мощность критерия вычисляется по
формуле (1
− β).
Таким образом, чем выше мощность, тем
меньше вероятность совершить ошибку
второго рода. уровень
значимости —
допустимая для данной задачи
вероятность ошибки
первого рода,
то есть того, что гипотеза на самом деле
верна, но будет отвергнута процедурой
проверки. Критической
областью называют совокупность значений
критерия, при которых нулевую гипотезу
отвергают. Областью принятия гипотезы
(областью допустимых значений) называют
совокупность значений критерия,
при которых гипотезу принимают.
.
Мощность критерия вычисляется по
формуле (1
− β).
Таким образом, чем выше мощность, тем
меньше вероятность совершить ошибку
второго рода. уровень
значимости —
допустимая для данной задачи
вероятность ошибки
первого рода,
то есть того, что гипотеза на самом деле
верна, но будет отвергнута процедурой
проверки. Критической
областью называют совокупность значений
критерия, при которых нулевую гипотезу
отвергают. Областью принятия гипотезы
(областью допустимых значений) называют
совокупность значений критерия,
при которых гипотезу принимают.
