
- •1.Предмет и задачи теории вероятностей. Пространство элементарных событий.
- •2. Случайные события и их классификация. Операции над событиями.
- •3 Частота появления случайного события и ее свойства.
- •4. Вероятность случайного события и её свойства
- •5.Статистическое, классическое, аксиоматическое и геометрическое опред вероятности случайного события.
- •6. Теоремы сложения вероятностей событий.
- •7.Теоремы умножения вероятностей событий. Условная вероятность. Независимость событий.
- •9.Схема испытаний Бернулли. Формула Бернулли. Производящая функция. Наивероятнейшее число наступления события.
- •10.Теоремы Муавра-Лапласа и Пуассона и их применение в схеме испытаний Бернулли.
- •11. Формула полной вероятности. Формула Байеса.
- •12. Определение случайной величины. Классификация случайных величин. Закон распределения случайной величины. Формы задания закона распределения дискретной св
- •13. Функция распределения и ее свойства.
- •14.Плотность вероятности случ величины и ее св-ва.
- •16. Биноминальное распределен и его числ. Хар-ки
- •18.Равномерное распределение и его числовые характеристики.
- •19. Показательное распределение и его числовые характеристики.
- •20. Нормальный закон распределения и его числовые характеристики. Функция Лапласа.
- •22.Теоремы Чебышева, Бернулли и Пуассона.
- •23. Центральная предельная теорема теории вероятностей и ее следствие.
- •24. Предмет и задачи мат. Статистики. Ген. И выборочная сов-ти. Формы записи исходных статистич. Данных. Статистический, вариационный и интервальный ряды и их хар-ки.
- •25.Графическое представление распределений.
- •26. Понятие оценки. Виды оценок. Свойства оценок. Точечные оценки параметров ген. Совокупности и методы их получения
- •27.Понятие интервальной оценки. Доверительный интервал и доверительная вероятность. Доверительный интервал для генеральной средней нормально распределенной сов-ти.
- •30. Критерии проверки параметрических и непараметрических гипотез: t-критерий, f –критерий, критерий согласия Пирсона, критерий согласия Колмогорова (самостоятельно).
- •32. Проверка гипотезы о числовом значении дисперсии признака в генеральной совокупности.
- •33.Проверка гипотезы о числовом знач доли признака в гс.
- •36. Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона.
- •37. Проверка гипотезы о показательном распределении генеральной совокупности с помощью критерия Пирсона.
- •38. Проверка гипотезы о равномерном распределении генеральной совокупности с помощью критерия Пирсона.
- •39.Проверка гипотезы о равномерном распределении генеральной совокупности с помощью критерия Колмогорова
- •40. Проверка гипотезы о распределении генеральной сов-ти по биномиальному закону с помощью критерия Пирсона.
- •41. Проверка гипотезы о распределении ген. Сов-ти по з-ну Пуассона с помощью критерия Пирсона.
- •42.Основные понятия дисперсионного анализа. Проверка гипотезы о равенстве генеральных групповых дисперсий. Критерий Бартлетта.
- •43.Проверка гипотезы о значимости влияния фактора на результативный признак с помощью дисперс анализа.
- •44. Проверка гипотезы о равенстве групповых средних с помощью дисперсионного анализа.
- •46.Выборочный парный коэффициент линейной корреляции, его свойства и значимость. Коэффициент детерминации, его свойства и интерпретация.
- •47.Выборочный множественный коэффициент корреляции, его свойства и значимость
- •48.Выборочные частный коэффициенты корреляции, их свойства и значимость. Матрица парных коэффициентов корреляции.
- •15. Основные и не основные числовые характеристики случайной величины, их свойства и способы их вычисления. (зр и чх св)
- •49. Понятие регрессии. Задачи регресс анализа. Модель регрессии. Линейная парная регрессия. Метод наим квадратов опред параметров линейного уравнения регрессии.
- •45 Понятие о линейной корреляции и регрессии. Представление данных в корреляционном анализе.
23. Центральная предельная теорема теории вероятностей и ее следствие.
Если случайные величины Х1…..Xn взаимонезависимы и одинаково распределены с конечными мат. Ожиданиями и конечными дисперсиями, то имеет место придельное соотношение
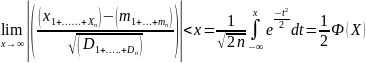
Смысл теоремы:
Если случайная величина представляет собой сумму очень большого числа взаимонезависимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало , то данная случайная величина Х имеет распределение близкое к нормальному.
Теорема Бернулли:
Если в каждом из n независимых испытаний вероятность появления некоторого события А есть величина равная Р в каждом из n испытаний, то при достаточно большом числе испытаний частота появления данного события сходится к вероятности его появления по сходимости от вероятности:
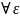 >0=>P
>0=>P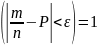
24. Предмет и задачи мат. Статистики. Ген. И выборочная сов-ти. Формы записи исходных статистич. Данных. Статистический, вариационный и интервальный ряды и их хар-ки.
Мат статистика - это раздел математики занимающийся изучением закономерностей которым подчиняются массовые явления на основе результатов наблюдений.
Предметом МС явл разработка методов регистрации описания и анализа экспериментальных данных получаемых в результате наблюдения массовых случайны величин.
Основной задачей МС является разработка методов получения научно обоснованных выводов о массовых явлениях и процессах по экспериментальным данным.
Определение 1 – совокупность значений какого либо признака объектов наз генеральной совокупностью, а совокупность объектов отобранных каким либо образом из ГС с целью их исследования наз выборочной совокупностью.
Определение 2 – выборочная совокупность называется репрезентативной если ее вероятные свойства совпадают или близки к вероятностным свойствам ГС.
Задача МС сводится к исследованию свойств выборки и обобщению этих свойств на всю ГС. Выбирая элементы выборки случайно, получается совокупность репрезентативной.
Выборка наз случайной если всем объектам ГС гарантированна одинаковая вероятность подвергнуться исследованию.
Выборка наз повторной или возвратной если исследования какого либо признака возвращается в ГС и наз бесповторной или возвратной.
Определение 3 – Выборочные значения исслед. признака записанные в порядке их регистрации называются простым статистическим рядом.
Определение 4 - выборочные значения исследуемого признака записанные в порядке возрастания их значений называется статистическим рядом.
Определение 5 – выборочные значения записанные в виде таблицы первой строкой которой явл объединенные значения признака в возрастающем порядке, а второй частота встречаемости данных вариант называется вариационным рядом или вариационной таблицей.
Определение 6 – таблица составленная из не пересекающихся интервалов вариант признака в первой строке и частот значений вариант попавших в каждый интервал во второй строке наз интервальным вариационным рядом.
25.Графическое представление распределений.
Гистограмма – ступенчатая фигура, сост из прямоугольников с основаниями, равными интервалам значен. вариант и с вычетом пропорц. частотами знач.
ni
xi
Полигон частоты – ломаная, сост из отрезков последоват соед точки (xi ,ni ) зн. вариант и их частот.
Примечание : гистограмма служит графическим представлением только инт. рядов, а полигон – как для интегральных, так и для вариационных.
П олигон для интегрального ряда: Полигон для вариационного ряда:

Эмпирическая функция распределения признака X в выборке называется ф-я, обозначаемая F*(x) и определяемая аналитическим выражением:
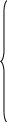
F (x) =


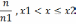
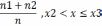
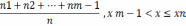
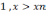
Модой выборки называется величина, обозначаемая μo,b и определяется как значение вар-ты,наиболее часто встреч. в выборке
Медианой выборки называется величина, обозначаемая μe,b и опред как среднее эксперим. значение в упорядоченном по возрастанию множестве эксперим. значений.
