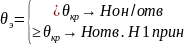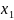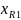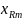- •1.Предмет и задачи теории вероятностей. Пространство элементарных событий.
- •2. Случайные события и их классификация. Операции над событиями.
- •3 Частота появления случайного события и ее свойства.
- •4. Вероятность случайного события и её свойства
- •5.Статистическое, классическое, аксиоматическое и геометрическое опред вероятности случайного события.
- •6. Теоремы сложения вероятностей событий.
- •7.Теоремы умножения вероятностей событий. Условная вероятность. Независимость событий.
- •9.Схема испытаний Бернулли. Формула Бернулли. Производящая функция. Наивероятнейшее число наступления события.
- •10.Теоремы Муавра-Лапласа и Пуассона и их применение в схеме испытаний Бернулли.
- •11. Формула полной вероятности. Формула Байеса.
- •12. Определение случайной величины. Классификация случайных величин. Закон распределения случайной величины. Формы задания закона распределения дискретной св
- •13. Функция распределения и ее свойства.
- •14.Плотность вероятности случ величины и ее св-ва.
- •16. Биноминальное распределен и его числ. Хар-ки
- •18.Равномерное распределение и его числовые характеристики.
- •19. Показательное распределение и его числовые характеристики.
- •20. Нормальный закон распределения и его числовые характеристики. Функция Лапласа.
- •22.Теоремы Чебышева, Бернулли и Пуассона.
- •23. Центральная предельная теорема теории вероятностей и ее следствие.
- •24. Предмет и задачи мат. Статистики. Ген. И выборочная сов-ти. Формы записи исходных статистич. Данных. Статистический, вариационный и интервальный ряды и их хар-ки.
- •25.Графическое представление распределений.
- •26. Понятие оценки. Виды оценок. Свойства оценок. Точечные оценки параметров ген. Совокупности и методы их получения
- •27.Понятие интервальной оценки. Доверительный интервал и доверительная вероятность. Доверительный интервал для генеральной средней нормально распределенной сов-ти.
- •30. Критерии проверки параметрических и непараметрических гипотез: t-критерий, f –критерий, критерий согласия Пирсона, критерий согласия Колмогорова (самостоятельно).
- •32. Проверка гипотезы о числовом значении дисперсии признака в генеральной совокупности.
- •33.Проверка гипотезы о числовом знач доли признака в гс.
- •36. Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона.
- •37. Проверка гипотезы о показательном распределении генеральной совокупности с помощью критерия Пирсона.
- •38. Проверка гипотезы о равномерном распределении генеральной совокупности с помощью критерия Пирсона.
- •39.Проверка гипотезы о равномерном распределении генеральной совокупности с помощью критерия Колмогорова
- •40. Проверка гипотезы о распределении генеральной сов-ти по биномиальному закону с помощью критерия Пирсона.
- •41. Проверка гипотезы о распределении ген. Сов-ти по з-ну Пуассона с помощью критерия Пирсона.
- •42.Основные понятия дисперсионного анализа. Проверка гипотезы о равенстве генеральных групповых дисперсий. Критерий Бартлетта.
- •43.Проверка гипотезы о значимости влияния фактора на результативный признак с помощью дисперс анализа.
- •44. Проверка гипотезы о равенстве групповых средних с помощью дисперсионного анализа.
- •46.Выборочный парный коэффициент линейной корреляции, его свойства и значимость. Коэффициент детерминации, его свойства и интерпретация.
- •47.Выборочный множественный коэффициент корреляции, его свойства и значимость
- •48.Выборочные частный коэффициенты корреляции, их свойства и значимость. Матрица парных коэффициентов корреляции.
- •15. Основные и не основные числовые характеристики случайной величины, их свойства и способы их вычисления. (зр и чх св)
- •49. Понятие регрессии. Задачи регресс анализа. Модель регрессии. Линейная парная регрессия. Метод наим квадратов опред параметров линейного уравнения регрессии.
- •45 Понятие о линейной корреляции и регрессии. Представление данных в корреляционном анализе.
41. Проверка гипотезы о распределении ген. Сов-ти по з-ну Пуассона с помощью критерия Пирсона.
Задано эмпирическое распределение дискретной случайной величины X. Требуется, используя критерий Пирсона, проверить гипотезу о распределении генеральной совокупности по закону Пуассона.
Правило. Для того чтобы при уровне значимости а проверитьгипотезу о том, что случайная величина X распределена по законуПуассона, надо:
1. Найти по заданному эмпирическому распределению выборочнуюсреднюю дгв.
2. Принять в качестве оценки параметра А, распределения Пуассона выборочную среднюю X = Xj^.
3. Найти по формуле Пуассона (или по готовым таблицам)
вероятности Pi появления ровно i событий в п испытаниях (i = 0,1,2,..., г,
где г — максимальное число наблюдавшихся событий; п — объем выборки/
4. Найти теоретические частоты по формуле п'^-п- Pi.
5. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона, приняв число степеней свободы k = s-2, где s — число различных групп выборки (если производилось объединение малочисленных частот в одну группу, то s — число оставшихся групп выборки после объединения частот).
42.Основные понятия дисперсионного анализа. Проверка гипотезы о равенстве генеральных групповых дисперсий. Критерий Бартлетта.
С помощью критериев, основан на сравнении дисперсии и на f(-статистики Фишера)
Постановка
задачи: Для задачь к выборок (R-выборов)
 i-I
i-I

 -извлечен
из распределений ГС требует. проверить
гипотезу о равенстве ГС Но=
-извлечен
из распределений ГС требует. проверить
гипотезу о равенстве ГС Но=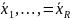 или
или
 или о значимости влияния ф-ра из 2 уровней
на результирующ. признак ГС.
или о значимости влияния ф-ра из 2 уровней
на результирующ. признак ГС.
 .
дисперсий всех ф-ов (всех ур.) по крит.
Бартл.
.
дисперсий всех ф-ов (всех ур.) по крит.
Бартл.
Пусть на результирующ.
признак оказывают влияние как ф-ых
признаков
 эксперементальн. данные R-тых
представлены табл-й
эксперементальн. данные R-тых
представлены табл-й
|
|
… |
|
|
|
… |
|
… |
… |
… |
… |
|
|
… |
|
Схема проверки
1) выделяются
гипотезы Но:
=…=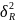 (генеральн. диспесии каждого из ур.=м/у
собой)
(генеральн. диспесии каждого из ур.=м/у
собой)

2) несмещен точечные
оценки ген. дисперс. ур-ний
 , гдне i=1-R
, гдне i=1-R
3) находится оценка
ген диспер. всех ур.
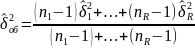
4) находится экспер.
знач. параметра
 статистики критерия Барл.
статистики критерия Барл.

5) Находит
эмперич. зн. критерия Бартл.

6) определяется кріт зн. статистики критерия Бартл.
 ,
,
 -задан. ур. значимости
-задан. ур. значимости
7)

43.Проверка гипотезы о значимости влияния фактора на результативный признак с помощью дисперс анализа.
Значимость фактора на результат признака
Схема проверки:
1) выдвигаются гипотезы Но=влияние фактора на результат не значима, т.е. случ. Н1: значимо, т.е. не случайно.
2) находится
∑результатов наблюдения на каждом из
ур.

i=1…k
3)находится ∑
результатов не всех ур. вместе

4) Находится ∑
квадратов наблюдений

5) Находится
ср. знач. ур-нь ∑квадр.
6) находится обяз. ср. ∑ квадратов
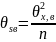 n=n+…+
n=n+…+

7)находится
несмещен. точечная общ. дисперсии всех
ур.
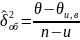
8)
-//- несмещ. течечн. оценка ф-рах

9)
экспер. зн. статистики критерия
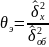
10)
опред. крит. зн. статистики критерия
 11)
11)