
РЯДЫ
1. Выражение
![]() (1)
называется рядом.
(1)
называется рядом.
Числовой ряд (1) называется сходящимся
если существует конечный предел его
частичных сумм.
![]() ,
S – сумма ряда.
,
S – сумма ряда.
Если такого предела не существует или
он равен
![]() ,
ряд называется расходящимся.
,
ряд называется расходящимся.
2. Для того чтобы ряд
![]() (1)
сходился необходимо выполнение условия.
Необходимо чтобы предел общего члена
ряда был равен 0.
(1)
сходился необходимо выполнение условия.
Необходимо чтобы предел общего члена
ряда был равен 0.
![]()
Доказательство:
Пусть ряд (1) сходится и S это предел его частичных сумм.
![]()
![]()
![]()
![]()
![]()
![]()
Рассмотрим предел
![]()
Эта теорема является необходимым но недостаточным условием сходимости ряда, т. е. может выполняться, а ряд может быть расходящимся.
3. Признаки сравнения положительных
рядов. Пусть даны два положительных
ряда
![]() и
и
![]() .
Тогда:
.
Тогда:
1) если
![]() при
всех n, то из сходимости
ряда
следует
сходимость ряда
,
а из расходимости ряда
следует
расходимость ряда
;
при
всех n, то из сходимости
ряда
следует
сходимость ряда
,
а из расходимости ряда
следует
расходимость ряда
;
2) если существует конечный
![]() ,
то ряды
и
сходятся
и расходятся одновременно;
,
то ряды
и
сходятся
и расходятся одновременно;
3)если
![]() при
всех n, то из сходимости
ряда
вытекает
сходимость ряда
,
а из расходимости ряда
вытекает
расходимость ряда
.
при
всех n, то из сходимости
ряда
вытекает
сходимость ряда
,
а из расходимости ряда
вытекает
расходимость ряда
.
4. Признак Даламбера.
Пусть для положительного ряда
существует
предел
![]() .
Тогда:
.
Тогда:
а) если l < 1, ряд сходится;
б) если l > 1, ряд расходится.
Доказательство:
1) Пусть l<1.
Рассмотрим число q, удовлетворяющее соотношению l < q < 1. (1)
Из определения предела и соотношения
(1) следует, что для всех значений n,
начиная с некоторого номера N, т. е. для
![]() ,
будет иметь место неравенство
,
будет иметь место неравенство
![]() (1').
(1').
Действительно, так как величина
![]() стремится к пределу l, то разность
между величиной
и числом l может быть сделана
(начиная с некоторого номера N) по
абсолютному значению меньше любого
положительного числа, в частности,
меньше, чем q-l, т. е.
стремится к пределу l, то разность
между величиной
и числом l может быть сделана
(начиная с некоторого номера N) по
абсолютному значению меньше любого
положительного числа, в частности,
меньше, чем q-l, т. е.
![]() .
.
Из последнего неравенства и следует неравенство (1'). Записывая неравенство (1') для различных значений n, начиная с номера N, получим:
![]() (2)
(2)
Рассмотрим теперь два ряда:
![]() (3)
(3)
![]() (3')
(3')
Ряд (3') есть геометрическая прогрессия
с положительным знаменателем q <
1. Следовательно, этот ряд сходится.
Члены ряда (3), начиная с
![]() ,
меньше членов ряда (3'). На основании
признака сравнения заключаем, что ряд
(3) сходится.
,
меньше членов ряда (3'). На основании
признака сравнения заключаем, что ряд
(3) сходится.
2) Пусть l>1. Тогда из равенства
(где l > 1) следует, что, начиная с
некоторого номера N, т. е. для
,
будет иметь место неравенство
![]()
или
![]() для всех
.
Но это означает, что члены ряда возрастают,
начиная с номера N + 1, и поэтому общий
член ряда не стремится к нулю. Следовательно,
ряд расходится.
для всех
.
Но это означает, что члены ряда возрастают,
начиная с номера N + 1, и поэтому общий
член ряда не стремится к нулю. Следовательно,
ряд расходится.
5. Признак Коши.
Пусть для положительного ряда
существует
предел
![]() .
Тогда:
.
Тогда:
а) если l<1, ряд сходится;
б) если l>1, ряд расходится.
Доказательство:
По определению предела для любого
![]() существует
существует
![]() начиная с которого выполняются неравенства
начиная с которого выполняются неравенства
![]()
1) l < 1
Выберем
![]() ,
чтобы
,
чтобы
![]() ,
тогда начиная с N, будет
выполняться неравенство:
,
тогда начиная с N, будет
выполняться неравенство:
![]()

![]() - сходится
- сходится
![]() - сходится
- сходится
геометрическая прогрессия
2) l > 1
Выберем
,
чтобы
![]() ,
тогда начиная с N, будут
выполняться неравенства:
,
тогда начиная с N, будут
выполняться неравенства:

![]() Нарушен необходимый признак сходимости
ряда, и он расходится.
Нарушен необходимый признак сходимости
ряда, и он расходится.
6. Интегральный признак Коши.
Пусть члены ряда
положительны
и не возрастают, т. е.
![]() ,
и пусть
,
и пусть
![]() - непрерывная невозрастающая функция,
определенная при
- непрерывная невозрастающая функция,
определенная при
![]() ,
такая, что
,
такая, что
![]() .
Тогда интеграл
.
Тогда интеграл
![]() и ряд
сходятся
или расходятся одновременно.
и ряд
сходятся
или расходятся одновременно.
Доказательство:
Для доказательства рассмотрим ряд
![]() ,
частичная сумма которого равна
,
частичная сумма которого равна
![]() .
.
Т. к. функция f(x)
невозрастающая, то
![]() .
Интегрируя это неравенство, получаем
.
Интегрируя это неравенство, получаем
![]() .
.
По признаку сравнения отсюда следует, что ряды и сходятся или расходятся одновременно.
Т.к.
![]() ,
то ряд
и
интеграл сходятся или расходятся
одновременно.
,
то ряд
и
интеграл сходятся или расходятся
одновременно.
7. Знакопеременные ряды. Условная и абсолютная сходимость.
Ряд называется знакопеременным,
если он имеет бесконечное число как
положительных, так и отрицательных
членов.
![]()
![]() (1)
(1)
Знакочередующийся ряд (1) называется сходящимся абсолютно если сходится ряд составленный из абсолютных величин его членов. Если ряд (1) сходится, а ряд составленный из абсолютных величин расходится, то говорят что этот ряд сходится условно.
8. Признак Лейбница.
Пусть для знакочередующегося ряда
![]() выполнены
условия:
выполнены
условия:
последовательность
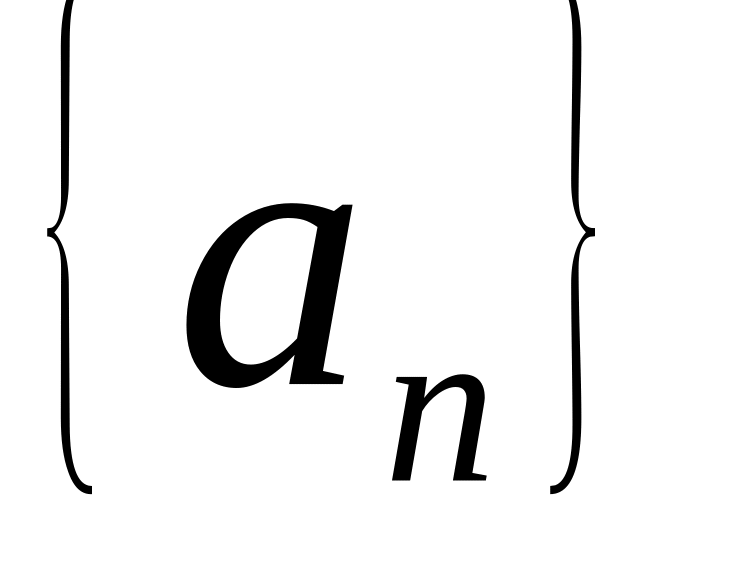 является невозрастающей, т. е.
является невозрастающей, т. е.
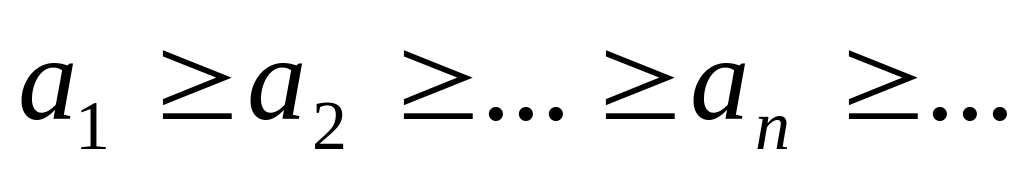 ;
;
Тогда ряд сходится.
Доказательство:
Рассмотрим подпоследовательность
частичных сумм ряда с четными номерами
![]() .
.
Представим ее в виде
![]() .
.
Отсюда следует, что последовательность
ограничена сверху числом
![]() :
:
![]() .
.
С другой стороны,
![]() может
быть представлена в виде
может
быть представлена в виде
![]() ,
откуда следует, что подпоследовательность
не
убывает.
,
откуда следует, что подпоследовательность
не
убывает.
Т. о., существует
![]() ,
т. к.
не
убывает и ограничена сверху.
,
т. к.
не
убывает и ограничена сверху.
Рассмотрим теперь подпоследовательность
с нечетными номерами
![]() :
:
![]()
Т. к. подпоследовательности
и
![]() сходятся к одному и тому же пределу S,
то вся последовательность частичных
сумм
сходятся к одному и тому же пределу S,
то вся последовательность частичных
сумм
![]() также
имеет предел
также
имеет предел
![]() и,
следовательно, ряд
сходится.
и,
следовательно, ряд
сходится.
Теорема Лейбница позволяет оценить количество слогаемых знакочередующегося ряда, которые нужно сложить чтобы получить его сумму с заданной точностью.
![]() -
сходится,
-
сходится,
![]()
9. Функциональные ряды. Область сходимости…
Рассмотрим функциональный ряд:
![]() (1)
(1)
где
![]()
![]() - функции, определенные на некотором
множестве А. Придавая х определенные
числовые значения, получаем различные
числовые ряды, которые могут оказаться
сходящимися или расходящимися.
- функции, определенные на некотором
множестве А. Придавая х определенные
числовые значения, получаем различные
числовые ряды, которые могут оказаться
сходящимися или расходящимися.
Совокупность значений х, при которых функциональный ряд (1) сходится, называют областью сходимости ряда.
Функциональный ряд (1) называется
мажорируемым на [a, в] если
существует такой сходящийся числовой
ряд
![]() ,
что для всех
,
что для всех
![]() выполняются:
выполняются:
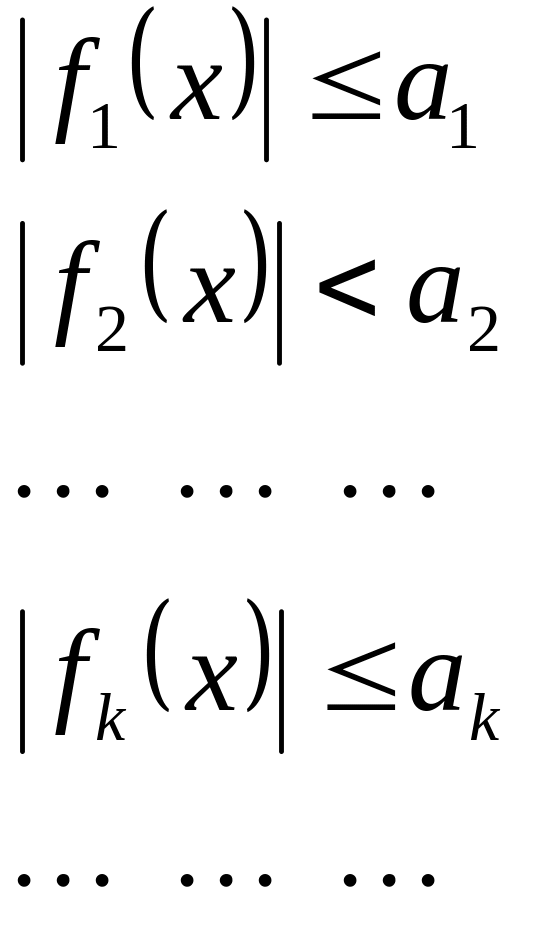
10. Интервал сходимости степенного ряда. Радиус.
Степенным рядом называется выражение:
![]() (1)
(1)
Те значения х при которых ряд (1) сходится называются областью сходимости степенного ряда.
Теорема Абеля.
Если степенной ряд (1) сходится при некотором значении
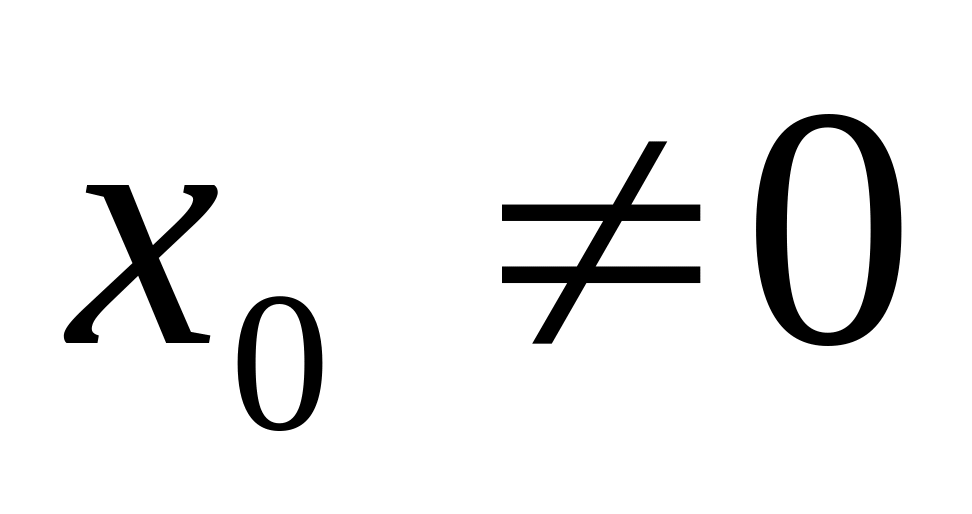 ,
то он сходится абсолютно при любом
значении
,
то он сходится абсолютно при любом
значении
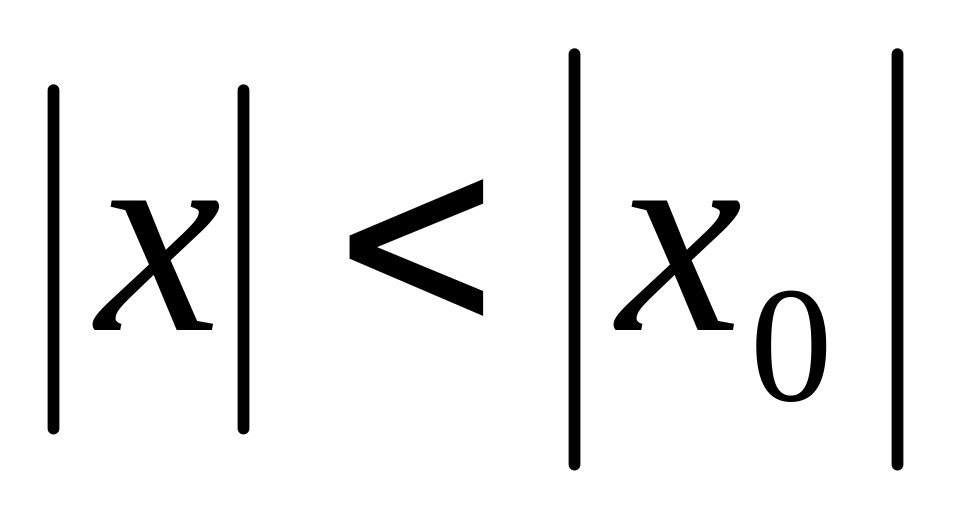 .
.Если ряд (1) расходится при некотором значении
 ,
то он расходится при любом
,
то он расходится при любом

Доказательство:
1) Согласно необходимому условию
сходимости числового ряда
![]() существует
такое M, что
существует
такое M, что
![]() .
Поэтому
.
Поэтому
![]()
При
ряд
![]() представляет
собой геометрическую прогрессию со
знаменателем меньше единицы, поэтому
он сходится. Следовательно, ряд
представляет
собой геометрическую прогрессию со
знаменателем меньше единицы, поэтому
он сходится. Следовательно, ряд
![]() сходится по признаку сравнения.
сходится по признаку сравнения.
2) Предположим противное. Пусть ряд
![]() сходится
в некоторой точке
сходится
в некоторой точке
![]() .
Тогда согласно первому утверждению ряд
сходится для всех
.
Тогда согласно первому утверждению ряд
сходится для всех
![]() ,
в том числе и в точке
.
А это противоречит условию. Следовательно,
ряд
расходится
при всех
.
,
в том числе и в точке
.
А это противоречит условию. Следовательно,
ряд
расходится
при всех
.
Теорема Абеля позволяет судить о
расположении точек сходимости и
расходимости степенного ряда. Из нее
следует, что существует такое число R
(оно может быть и 0, и
![]() ),
что ряд абсолютно сходится при
),
что ряд абсолютно сходится при
![]() (если
(если
![]() )
и расходится при
)
и расходится при
![]() (если
(если
![]() ).
Число R называется
радиусом сходимости степенного
ряда, а интервал
).
Число R называется
радиусом сходимости степенного
ряда, а интервал
![]() - интервалом сходимости.
- интервалом сходимости.
Вывод формулы радиуса:
Для этого рассмотрим абсолютный ряд
.
Для каждого фиксированного х применим
к абсолютному ряду признак Даламбера:

Пусть
![]() .
Тогда по признаку Даламбера абсолютный
ряд сходится, если
.
Тогда по признаку Даламбера абсолютный
ряд сходится, если
![]() ,
и расходится при
,
и расходится при
![]() .
Следовательно исходный ряд сходится
абсолютно при
.
Следовательно исходный ряд сходится
абсолютно при
![]() и расходится при
и расходится при
![]() .
Т. о. число L является
радиусом сходимости, т. е.
.
Т. о. число L является
радиусом сходимости, т. е.
![]()
11. Свойства степенных рядов. Абсолютная сходимость, интегрируемость и дифференцируемость.
Свойства:
1) Сумма
![]() степенного ряда
степенного ряда
![]() (1) является непрерывной функцией в
каждой точке интервала сходимости
(1) является непрерывной функцией в
каждой точке интервала сходимости
![]() .
.
2) Ряд
![]() (2) полученный почленным дифференцированием
ряда (1), является степенным рядом с тем
же, что и ряд (1), интервалом сходимости
.
Сумма ряда (2)
(2) полученный почленным дифференцированием
ряда (1), является степенным рядом с тем
же, что и ряд (1), интервалом сходимости
.
Сумма ряда (2)
![]() .
.
3) Пусть числа
![]() и
и
![]() принадлежат интервалу сходимости
ряда (1). Тогда имеет место равенство:
принадлежат интервалу сходимости
ряда (1). Тогда имеет место равенство:
![]()
Теорема Абеля.
Если степенной ряд (1) сходится при некотором значении , то он сходится абсолютно при любом значении .
Если ряд (1) расходится при некотором значении , то он расходится при любом
Доказательство:
1) Согласно необходимому условию сходимости числового ряда существует такое M, что . Поэтому
При ряд представляет собой геометрическую прогрессию со знаменателем меньше единицы, поэтому он сходится. Следовательно, ряд сходится по признаку сравнения.
2) Предположим противное. Пусть ряд сходится в некоторой точке . Тогда согласно первому утверждению ряд сходится для всех , в том числе и в точке . А это противоречит условию. Следовательно, ряд расходится при всех .
12. Ряд Тейлора и Маклорена.
Если функция
имеет производные любого порядка в
окрестности точки
![]() ,
то получим бесконечный ряд, который
называется рядом Тейлора:
,
то получим бесконечный ряд, который
называется рядом Тейлора:
![]()
При
![]() получим частный случай ряда Тейлора,
который называют рядом Маклорена:
получим частный случай ряда Тейлора,
который называют рядом Маклорена:
![]()
13. Тригонометрический ряд. Ряд Фурье. Условие сходимости.
![]() (1)
(1)
Функция
![]() называется кусочно-монотонной на [
;
]
если существует конечное число точек
принадлежащих этому отрезку
называется кусочно-монотонной на [
;
]
если существует конечное число точек
принадлежащих этому отрезку
![]() таких, что на каждом частичном интервале
таких, что на каждом частичном интервале
![]() функция
непрерывна и монотонна.
функция
непрерывна и монотонна.
Тригонометрический ряд (1) называется
рядом Фурье функции
на отрезке
![]() если его коэффициенты определяются
следующим образом:
если его коэффициенты определяются
следующим образом:
![]()
![]()
![]()
Теорема.
Если
обладает кусочной дифференцируемостью
на отрезке [a; в],
то в каждой точке ряд Фурье сходится и
имеет сумму
![]() , где
, где
![]() -
односторонние конечные пределы слева
и справа.
-
односторонние конечные пределы слева
и справа.
Во всех точка непрерывности ряд Фурье сходится к этой функции.
Теорема формулирует достаточные условия сходимости ряда, а именно: в точках непрерывности сумма ряда равна , а в точках разрыва – полусумме односторонних пределов функции .
