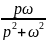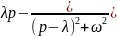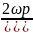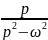- •Непрерывность и дифференцируемость комплексных переменных
- •П1.1 Предел последовательности комплексных чисел.
- •Свойства аналитической функции:
- •Тема 2: Интегрируемые теоремы. Интегральная форма
- •Свойства интегралов:
- •Тема: Оценка интеграла.
- •Свойства непрерывных функций:
- •Доказательство:
- •Доказательство:
- •Доказательство:
- •П(7.1) Локальные свойства отображения регулярных функций
- •Теорема Лема Шварца
- •П. (7.2) Общие свойства конформных отображений
- •Преобразование Лапласа.
- •Свойства преобразований Лапласа:
- •9) Изображение свёртки.
- •Метрические и топологические пространства.
- •Мера, интеграл Лебега
Преобразование Лапласа.
П(8.1) Преобразование Лапласа оригинал и изображение.
Пусть функция действительной переменной f(z)- определена при t≥0.
Определение:
Преобразование Лапласа называется
функция комплексной переменной. F(p)= (8.1)
(8.1)
Рассмотрим
комплекснозначную функцию
 заданную на всей действительной оси и
удовлетворяющую условию:
заданную на всей действительной оси и
удовлетворяющую условию:
1)На любом конечном интервале оси t, функция f(t)-неприрывна, кроме конечного числа точек разрыва первого рода.
2)f(t)=0, при t<0
3)Существуют
такие постоянные C
и α, что для всех t>0
выполняется неравенство:
|f(t)|≤C (8.2)
(8.2)
Определение: Функция f(t) удовлетворяет условиям (1-3) называется оригиналом, а её преобразование Лапласа f(t) – изображение функции F(ρ).
Пример:
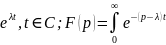 dt=
dt= (8.4) Сводится Re>Reλ.
(8.4) Сводится Re>Reλ.
Т(8.1)
Для всего оригинала f(t)
его изображение F(p)-
является регулярной функцией в
полуплоскости Re
p>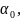 где
где
 показатель
роста F(p).
показатель
роста F(p).
Следствие:
Если F(t)
оригинал, то

Свойства преобразований Лапласа:
1)Линейность. Если f(t)↔G, g(t)↔G, то для любых λ и μ комплексных чисел справедлива комбинация: λf(t)+μg(t)↔λF(p)+μG(p); Это свойство следует из свойства интегралов.
2)
Подобие. Если
f(t)↔F(p),
то для любого σ>0, f(σt)↔
3)Дифференцирование
интеграла.
Если f(t),
f’(t),…,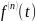 -
оригиналы, f(t)↔F(p);
-
оригиналы, f(t)↔F(p);
↔ -
- -
-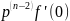 -…-
-…-
 -
-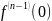 (8.5);
(8.5);
 =
=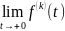 .
.
4)Дифференцирование
изображения. Если
f(t)↔F(p),
то ↔
↔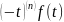 (8.6);
(8.6);
5)
Интегрирование оригинала. Если
f(t)↔F(p),
то
 (8.7);
(8.7);
6)
Интегрирование изображения.
Если f(t)↔F(p),
и если :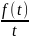 -
оригинал,
то
↔
-
оригинал,
то
↔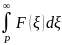 (8.8)
(8.8)
7)
Запаздывание оригинала. Если
f(t)↔F(p),и
f(t)=0,
при t<τ,
τ>0, то f(t-τ)↔ F(p)(8.9)
F(p)(8.9)
8)
Смещение изображения. Если
f(t)↔F(p),
для любого λ принадлежащего множеству
комплексных чисел, то
 (8.10)
(8.10)
9) Изображение свёртки.
Определение:
Свёрткой
функции f
и g
называется функция, которая обозначается
f*g
и определяется равенством:
(f*g)(t)=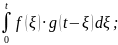 (f*g)(t)↔F(p)·G(p)
(8.11);
(f*g)(t)↔F(p)·G(p)
(8.11);
Таблица оригиналов и изображений часто встречается на практике:
1 |
|
|
|
|
|
|
|
Cos ωt |
|
Sin ωt |
|
|
|
|
|
tsinωt |
|
t cos ωt |
|
Ch ωt |
|
Sh ωt |
|
Т(8.2)
Пусть f(t)-
оригинал, а F(p)-его
изображение, если функция f(t)-неприрывна
в точке t
и имеет в этой точке конечные односторонние
производные, то:
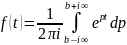 (8.12)
(8.12)
Интеграл
(8.12) берётся вдоль любой прямой Re
p=b> ,
где
-
показатель роста функции f(t)
и понимается в смысле главного значения.
,
где
-
показатель роста функции f(t)
и понимается в смысле главного значения.
Метрические и топологические пространства.
П(9.1) Метрические пространства.
Определение: Многие фундаментальные факты анализа опираются только на расстояние между числами, а не на их алгебраическую структуру.
Определение: Метрическим пространством называется пара (x,ρ) состоящая из некоторого множества пространства х-элементов (точек) и расстояния, т.е. однозначной неотрицательной действительной функцией ρ(x,y) определённой для любых х и у из множества Х и подчинённой следующим аксиомам:
ρ(x,y)=0 ↔ x=y
ρ(x,y)=ρ(y,x) аксиома симметрии
ρ(x,z)≤ ρ(x,y)+ ρ(y,z) аксиома треугольника
Если нет недоразумений будем означать пространство (х,ρ)→х, помня при этом, что есть метрика ρ.
Пример:
Множество упорядоченных наборов из n
действительных чисел х=(х…..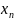 )
c
расстоянием ρ(x,y)
=
)
c
расстоянием ρ(x,y)
= (9.1)
называется
n-мерным
арифметическим Евклидовым пространством
(9.1)
называется
n-мерным
арифметическим Евклидовым пространством

Пусть Х и У метрические пространства ℓ: Х→У отображение. Для любого хϵХ, f(x)ϵY
Определение:
Отображение f
– называется непрерывным в точке
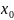 ϵх
, если для любого
ϵх
, если для любого
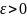 существует
σ>0 что для всех хϵХ таких что: ρ(x,
)<σ,
следует
существует
σ>0 что для всех хϵХ таких что: ρ(x,
)<σ,
следует
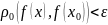
ρ расстояние в х, ρ1-расстояние в У
Если отображение f непрерывно при всех х∊Х, то она называется непрерывным на Х.
Определение:
Открытым шаром В(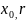 )
в метрическом пространстве R
(
)
в метрическом пространстве R
( )
мы будем называть совокупность точек
)
мы будем называть совокупность точек
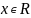 ,
удовлетворяющих условию: ρ(x,
)<r
при этом точка
-центр
этого шара, а число r-его
радиусом.
,
удовлетворяющих условию: ρ(x,
)<r
при этом точка
-центр
этого шара, а число r-его
радиусом.
Определение: Замкнутым шаром В( ) мы назовём совокупность точек , удовлетворяющих условию ρ(x, )≤r
Определение:
Открытый шар B(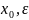 )
называется
)
называется
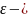 окрестностью
точки
окрестностью
точки
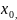 обозначают также B(
)
=
обозначают также B(
)
=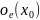
Множество МϵR называется ограниченным, если оно содержится целиком в некотором шаре.
Определение: Точка хϵR называется точкой прикосновения множества МϵR, если любая её окрестность содержит хотя бы одну точку из М.
Определение: Совокупность всех точек прикосновения для множества М называется замыканием множества М и обозначается [M].
Т(9.1) Операция замыкания обладает следующими свойствами:
М<[M].
[[М]]= [M].
Если М1ϵМ2 следовательно[M1]ϵ [M2].
Определение: Точка хϵR называется предельной точкой МϵR, если любая её окрестность содержит бесконечно много точек из М.
Определение:
Последовательность { }
сходится к х, если
}
сходится к х, если
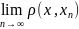 =0
=0
Т.(9.2) Для того, чтобы точка х была точкой прикосновения множества М необходимо и достаточно чтобы существовала последовательность { } точек из М, сходящихся к х (существует { }→x) ϵМ.
Определение: Множество А называется плотным в В, если [A]ϵB
Определение: Множество М, лежащее в метрическом пространстве R называется замкнутым, если оно совпадает со своим замыканием.
Т(9.3)Пересечение любого числа и сумма любого числа замкнутых множеств есть замкнутое множество.
Определение:
Точка х называется внутренней точкой
множества М, если существует окрестность
О (х)
этой точки целиком содержащейся в М.
(х)
этой точки целиком содержащейся в М.
Определение: Множество, у которого все точки внутренние называется открытым.
Т.(9.4) Для того, чтобы множество М было открыто необходимо и достаточно чтобы его дополнение до всего пространства R было замкнуто.
Дополнение:
(-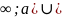 -
замкнутое пространство.
-
замкнутое пространство.
Т.(9.5) Сумма любого конечного или бесконечного числа и пересечение любого числа(конечного) открытых множеств есть открытое множество.
П.(9.2) Топологические пространства.
Можно на некотором пространстве R не вводить расстояние, а просто объявить некоторые множества открытыми, а некоторые замкнутыми.
Определение:
Пусть Х-некоторое множество, топологией
х называется любая система
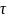 его полу множеств, удовлетворяющих 2-м
требованиям:
его полу множеств, удовлетворяющих 2-м
требованиям:
1.Само
множество Х, ф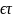
2.Сумма
по
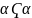 любого конечного или бесконечного и
пересечения любого
любого конечного или бесконечного и
пересечения любого
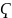 к
любого конечного числа множеств из
принадлежащих
к
любого конечного числа множеств из
принадлежащих
 т.е.
к
.
т.е.
к
.
Определение: Множество Х заданной в нём топологии в , т.е. пара (х, ) называется топологическим пространством.
Множество принадлежащее системе называется открытым.
Определение:
Окрестностью точки х из Т называется
открытое множество
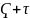 ,
содержащее точку х, х
,
содержащее точку х, х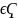 .Точка х из Т называется точкой
прикосновения множества М леж. в Т, если
каждая окрестность точки х, содержит
хотя бы одну точку из М.
.Точка х из Т называется точкой
прикосновения множества М леж. в Т, если
каждая окрестность точки х, содержит
хотя бы одну точку из М.
Определение: Совокупность всех точек прикосновения множества М называется замыканием множества М и обозначается [М].
Определение: Свойство L открытых полу множеств называется базой топологии пространства Т, если всякое открытое множество в Т может быть представлена как сумма некоторого числа конкретного или бесконечному множеству из L.
Свойство базы L:
1.Любые точки х из пространства Х содержатся хотя бы в GϵL
2.Если
х содержится в пересечении 2-х множеств
G1,G2
ϵL,
то существует G3ϵL,
что хϵG3ϵG G2
G2
Т.(9.2) Для того, чтобы система Lϵτ была базой для данной топологии τ необходимо и достаточно следующее условие:
3.Для каждого открытого множества G и каждой точки х из G существует такое Gх ϵ L , что хϵGхϵG
Определение:
Пусть Х и У два топологических пространства,
отображение f:
Х→У называется непрерывным в точке
, если для любой окрестности
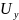 в точке
в точке
 найдётся
такая окрестность
найдётся
такая окрестность
 в точке
,
что f(
)ϵ
в точке
,
что f(
)ϵ

Т.(9.7)
Для того, чтобы отображение F
топологического пространства Х в
топологическое пространство У было
непрерывным необходимо и достаточно,
чтобы преобразование F= всякого открытого множества GϵУ
было открыто в Х.
всякого открытого множества GϵУ
было открыто в Х.
П.(9.3) Обобщённые функции.
При
некоторых физических задачах понятие
функций как правило ставящего в
соответствие каждому х некоторое
значение y=f(x)
не достаточно. Например, по прямой
задаётся распределение масс. Если
некоторая точка имеет положительную
массу, то плотность такого распределения
не может быть задана обычной функцией.
Пусть f-фиксир.,
интегрируемая функция на прямой fϵL.
 -неприрывная
функция,
-неприрывная
функция,
 С[a,b],
превращается в нуль вне некоторого
интервала. Такие функции называются
финитами. Каждой
сопоставим
число
С[a,b],
превращается в нуль вне некоторого
интервала. Такие функции называются
финитами. Каждой
сопоставим
число
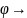 (f,
)
=
(f,
)
= (9.2)Т.о.
задан некий функционал на множестве
финитных функций, но можно рассматривать
другой линейный функционал, не задаваемый
в виде (9.2). Так мы приходим к понятию
обобщённых функций.
(9.2)Т.о.
задан некий функционал на множестве
финитных функций, но можно рассматривать
другой линейный функционал, не задаваемый
в виде (9.2). Так мы приходим к понятию
обобщённых функций.
Рассмотрим
прямую совокупность к всех финитных
функций
 имеющих
непрерывные производные всех порядков.
имеющих
непрерывные производные всех порядков.
Определение:
Последовательность { }
элементов из к называются сходящимися
к функции
}
элементов из к называются сходящимися
к функции
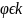 ,
если :
,
если :
1.Существует интервал, где все =0
2.
Последовательность
 производных, сходятся на этом интервале
равномерно,
→
(п)ϵ
(n)
производных, сходятся на этом интервале
равномерно,
→
(п)ϵ
(n)
Линейное пространство к называется основным пространством, а его элементы основными функциями.
Определение: Обобщённые функции на (-∞;+∞) называется непрерывный факториал Т( )
на основном пространстве к. При этом непрерывность факториала понимается в том смысле, что Т( к) сходится к Т( ):Т( n)→ɣ( ), если к→ .
Каждая интегрируемая функция F задаёт факториал: Тf( ):
Определение: Такие обобщённые функции называются регулярными (9.3), а функции не представленные в виде (9.3) называются ингумерными.
Определение:
Последовательность
обобщённых функций {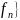 называется сходящейся к f:
{
→f,
если для любых φϵ k
:
называется сходящейся к f:
{
→f,
если для любых φϵ k
:
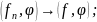
Определение: Если α- бесконечно дифференцируемая функция, то положим, что: αf:(αf,φ)=(f,αφ)
Определение:
 обобщение функции Т называется факториал,
dx
определяется формулой:
обобщение функции Т называется факториал,
dx
определяется формулой:
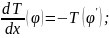
Свойства:
1)Всякая обобщённая функция имеет производные всех порядков.
2)Если
последовательность обобщённых функций
{ сходится к общей функции f,
то последовательность производных {
сходится к общей функции f,
то последовательность производных {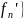 сходится к производной f’
последовательных функций.
сходится к производной f’
последовательных функций.
3)Всякий сходящийся ряд из общих функций можно дифференцировать почленно любое число раз.
П(9.4) Гильбертово пространство.
Рассмотрим бесконечномерное пространство, в котором есть счётное всюду плотное пространство.
Определение:
Метрическое пространство (x,ρ)
называется полным, если для любой
последовательности Коши { имеет предел
имеет предел

Определение: Полное Евклидово пространство бесконечного числа измерений называется Гильбертово пространство т.е. множество к- называется гильбертовым пространством если:
Н –есть евклидово пространство.
Пространство можно представить в смысле метрики: ρ(f,g)=||f-g||
Пространство H бесконечномерно, т.е. для любых n в нём можно найти n-мерно-независимых векторов.
Н- сепарабельно, т.е. в нём существует всюду плотное множество.
Обозначим
через
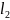 метрическое пространство с последовательности
(
метрическое пространство с последовательности
(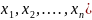 ,
,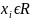 таких что:
таких что: .
Рассмотрим в нём определение формулой:
ρ(x,y)=
.
Рассмотрим в нём определение формулой:
ρ(x,y)=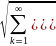 (9.5)
(9.5)
Определение:
Два евклидовых пространства R, -называются
изолированными, если есть взаимно-однозначное
соответствие между их элементами: такое
что, если x⇒
-называются
изолированными, если есть взаимно-однозначное
соответствие между их элементами: такое
что, если x⇒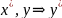 .
y,xϵR,
.
y,xϵR,
 ;
x+y↔
;
x+y↔ ;
αx↔α
;
αx↔α
Т(9.8) Любые два сепарабельных Гильбертовых пространства изолированы между собой.