Непрерывность и дифференцируемость комплексных переменных

Понятие комплексного числа возникло с автоматизацией вычислений. Известно, что не все полиномы с действительными коэффициентами имеют действительные корни, поэтому приходиться разбирать варианты, когда имеются корни, а когда нет. Введение понятия комплексного числа существенно упростило вычисление, основная теорема алгебры утверждала, что многочлены с комплексными членами имеют комплексные корни.

П1.1 Предел последовательности комплексных чисел.

Определение последовательности, сходящейся последовательности комплексных чисел повторяют определение теории функции действительной переменной.

Определение: Последовательностью комплексных чисел называется перенумерованное бесконечное множество комплексных чисел, обозначается {Zn}

Комплексные числа {Zn}, образующие последовательность, называются её элементами.

Определение: Число Z называют пределом последовательности {Zn}, если для любого положительного числа ε можно указать такой номер N(ε) начиная с которого все элементы {Zn} этой последовательности удовлетворяют неравенству: для любого ε > 0, существует N(ε) n такое что |Z-Zn|< ε, при n ≥ N(ε) (1.1)

Последовательность {Zn} ,имеющая предел Z, называется сходящейся к числу Z, что записывается в виде: 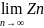=Z

Определение: Множество точек Z комплексной плоскости, лежащих внутри окружности радиусом ε, с центром в точке Zо, |Z-Zо|< ε называется ε-окрестностью точки Zо. Другими словами число Z является пределом последовательности Zn, если в любой ε-окрестности точки Z лежат все члены последовательности, начиная с некоторого члена.

Т1.1 : Необходимым и достаточным условием сходимости последовательности Zn является сходимость последовательности действительных чисел {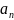 }, { } 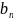(Zn= )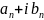

Определение: Последовательность Zn называется ограниченной, если существует такое положительное число М, что для всех элементов Zn этой последовательности выполняется |Zn|<M т.е.: существует М такое, что для любого Zn: |Zn|<M

Т1.2: Из всякой ограниченной последовательности можно выделить сходящуюся под неё последовательность. При исследовании последовательностей часто используют необходимый и достаточный признак сходимости последовательности, называется критерий Коши.

Т1.3 Критерий Коши: Последовательность Zn сходится тогда и только тогда, если для любого ε>0 существует N(ε) такое что |Zn-Zn+m|<ε при n≥ N(ε), для любого m≥0 (1.2)

Введём понятие бесконечно удалённой точки

Пусть дана последовательность {Zn} такая что для любого положительного числа R>0 существует N такое что |Zn|>R,n≥N, такая последовательность называется неограниченно возрастающей, она не сходится в силу определения сходимости, однако мы будем считать что она расходится к комплексному числу Z, т.е. Zn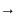 Z=∞

Всякая неограниченно возрастающая последовательность сходится к этому числу. Полная комплексная плоскость состоит из обычной комплексной плоскости и числа бесконечности.

а)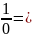 ∞; б)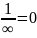 ; в)z*∞=∞, при z≠0; г)z+∞=∞; д)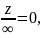 при z≠∞

Эти равенства естественны с точки зрения предельного перехода

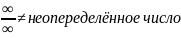
п1.2 Непрерывность функции комплексной переменной.

На множестве {E} комплексной плоскости задана функция комплексной переменной, если задан закон, ставящий соответствие в каждой точке множества Е некоторое комплексное число. Структура множества Е может быть очень сложной поэтому нам потребуется понять понятие области.

Определение: Точка Z называется внутренней точкой {E}, если существует ε-окрестность точки Z, все точки которой принадлежат множеству Е.

Определение: Множество {E} называется областью, если выполняются условия:

1)каждая точка множества Е-это внутренняя точка этого множества;

2)любые 2 точки множества Е можно соеденить ломаной, все точки которой принадлежат Е.

Множество точек |z|<1 являются областью, а множество точек |z|≤1 не являются областью. Т.к. не все точки являются внутренними.

Множество точек |z|<1 либо |z-4|<2 не являются областью т.к. свойство (2) не выполняется.

Для обозначения области используем буквы:G,D,Eи т.д.

Определение: Точка z называется внешней точкой, если существует такая ε окрестности точки z все точки, которой не € D.

Определение: Точка z называетcя граничной точкой области D, если в любой её ε окрестности содержащей как точки принадлежащие области D, так и точки не принадлежащие области D.

Например: точка z=1 является граничной для области |z|=1

Определение: Множество полученное присоединением к области всех её граничных точек называется замкнутой областью. Обозначается: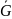 , 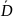и т.д.

Определение: Если область D лежит целиком внутри некоторого круга конечного радиуса, то она называется ограниченной, в противном случае – неограниченной.

Определение: Однозначная функция комплексной переменной z заданной в области D в соответствии с определённым числом W т.е.

W=f(z) (1.3)

Выделив действительную и мнимую часть чисел W можно записать:

W(z)=u(x,y)+iv(x,y) (1.4)

U(x,y)- действительная часть

V(x,y)-мнимая часть

Часто рассматривают функции, когда одному z ставится в соответствии множество значений.

W=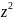 Такие функции называются многозначными.

Определение: функция f(z) называется однолистной функцией в области D, если в различных точках z этой области она принадлежит разным значениям.

Однолистная функция осуществляет взаимно однозначное соответствие, обратимая функция z=ϕ(w) является однозначной.

Определение: Если независимая от выбора последовательность {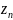 } существует единичный предел: 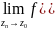)= 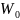, то этот предел называется пределом функции f(z) в точке .

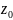)= (1.5)

Определение: Функция f(z) заданная на {E} называется непрерывной в точке ϵE, если знач. Этой функции в точке существует конечно и совпадает со значением f( ) функции f(z) в точке т.е.

)=f( ).

Пример: f(z)=az+b, a,b ϵ c a≠0

W=f(z)=az+b,

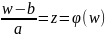
Значит функция f(z) однолистная, осуществляется взаимно однозначное соответствие плоскостей z и w, функция эта является непрерывной, т.к. при

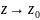
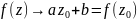
П1.3 Дифференцирование функций комплексной переменной.

До сих пор была полная аналогия с теорией функций действительной переменной, понятие дифференцирование приводит к существенным различиям. Пусть в области Д задана функция F(z).

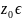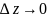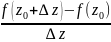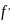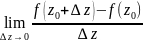Определение: Если для точки Д существует при предел отношения , то этот предел называется производной функции f(z) по комплексной переменной в точке и обозначается ( ) , т.е. ( )= (1.6)

Функция f(z) называется дифференцируемой в точке , если выполняется условие Коши-Римана:

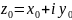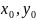Т1.4 Если функция f(z) дифференцируема в точке ,то в точке ( ) существует частная производная функций u(x,y) и v(x,y) по переменным x и y, причём имеет место соотношение:

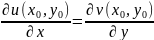
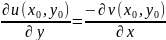(1.7) условие Коши-Римана

Т(1.5) Если в точке( )функции u(x,y) и v(x,y) дифференцируемы, а их частные производные произвольно связанны с соотношением (1.7), то функция f(z)= u(x,y) +v(x,y) является дифференцируемой функцией комплексной переменной .

Определение: Если функция f(z) дифференцируема во всех точках области Д, а её производная непрерывна в этой области, то функция f(z) является аналитической функцией в области Д. Понятие аналитической функции является основной в ТФКП.