8. Момент силы. Основной закон механики вращательного движения.

Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).

Законы динамики вращательного движения

а) Закон инерции-торможения вращения

Используя принцип аналогий, с учетом первого закона ИМ (инерции-торможения) покажем закон инерции –торможения вращения для вращающихся систем

М ин - Мторм = d L / dt , (10)

где М ин - момента инерции вращения, М торм – момент торможения при вращении.

Из (10) вытекает самое главное свойство Инерции вращающейся материи.

Скорость изменения момента импульса вращения L вращающегося м.т. в инерциальном вращении равна действию на него разности моментов инерции Мин и момента торможения Мторм.

Вращение по инерции будет происходить с торможением, так как на вращающееся тело действует полевая материя, которая будет тормозить вращение до момента начала действия периодического внешнего момента сил.

б) Закон инертного ускорения вращения

Используя принцип аналогий, с учетом 2-го закона ИМ (инертности ускорения) покажем закон инертного ускорения вращения для вращающихся систем

Муск – Минт = dL/dt (11)

Скорость изменения момента импульса вращения L вращающегося м.т. в ускоренном вращении равна действию на него разности моментов ускорения Муск и инертного момента Минт .

в) Закон противодействия моментов сил при вращении

Используя принцип аналогий, с учетом третьего закона противодействия ИМ, покажем в виде закона противодействия моментов сил при вращении м.т.

Мвн = - k L w , (12)

где Мвн - внешний момент действующих сил на вращающуюся систему типа (НС+СП), Мпрот - внутренний момент противодействия вращению равный k Lw, где k-коэффициент противодействия вращению.

Если на вращающееся м.т. 1 со стороны другого м.т. 2 действует момент вращения, то в первом теле возникает момент вращения противоположный по направлению моменту вращения м.т. 2 и пропорциональный ему по величине.

9. Определение периода колебаний математического маятника. Гармонические колебания.

Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины l неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен

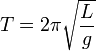
и не зависит^[1] от амплитуды и массы маятника.

Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью.

При малых колебаниях физический маятник колеблется так же, как математический с приведённой длиной.

Гармонические колебания

Маятник, совершающий малые колебания, движется по синусоиде. Поскольку уравнение движения является обыкновенным ДУ второго порядка, для определения закона движения маятника необходимо задать два начальных условия — координату и скорость, из которых определяются две независимых константы:

где A — амплитуда колебаний маятника, θ₀ — начальная фаза колебаний, ω — циклическая частота, которая определяется из уравнения движения. Движение, совершаемое маятником, называется гармоническими колебаниями