Если рассматривается сложная система, состоящая из нескольких подсистем, независимых друг от друга, то энтропия всей системы будет равна сумме энтропий подсистем. Если подсистемы зависимы друг от друга, то это правило не выполняется. В этом случаи определить энтропию всей системы более сложно. Имеется теорема, в соответсвии с которой энтропия объединенной системы будет всегда меньше, чем энтропий объединяемых у системе. Для того чтобы определить на сколько меньше, используется понятие условной энтропии. Пусть имеетвс я две системы: X, Y. В общем случаи зависимые. парковкой

Вероятность того, что система У примит j состояние. Условная энтропия завсит от того какое состояние приняла система Х, для одних состояний больше, других меньше. Можно определить среднюю или полную энтропию системы У, с учетом того, что система Х может принимать разные состояния. Средняя или полная условная энтропия и сооответсвенно средняя или полная информация будет равна мат ожиданию количества информации получаемого от возможных частных сообщений.

Можно рассмотреть две зависимые системы и информацию содержащуюся в систем У по системе Х, тПре. можно судить о системе Х наблюдая за сисетмой У. Такая ситуация встречается на практике очень часто, например, к ней относятся практически любые измерения, когда мы судим о системе по показаниям приборов, изучаемый объект является система Х, а прибор система У.

Имеется понятие полной информации - полная информация о системе Х содержащаяся у системе У. Имеется теорема согласно которой

Если система Х и У независмы, то полная взаимная информация равна 0. Если состояние системы Х полностью определяется состояниями системы У, и наоборот, то тогда полная взаимная информация будет равна энтропии каждой из систем.

Рассматриваются подчиненные системы, т.е если состояние системы полностью определяется состоянием другой системы, то такая система называется подчиненой. Для таких систем полная взаимная информация будет равна энтропии подчиненной системы. Как измвестно из курса информатики, если имеется алфавит состоящий из n символов и мы записываем слово состоящее из m символов этого алфавита, то всего можно записать N = n^m сообщений, в частности для бинарной системы N = 2^m. Максимально возможная энтргпия сообщения состоящего из m букв n буквенного сообщения будет равна , например, максимально возоможного сообщения состоящего из 5 букв 32 буквенного алфавита будет равна 25 бит.

Если наблюдается система У, по этим наблюдениям судят по системе Х, то различия будут возникать по следующим двум причинам:

1. Некоторые состояния системы Х не находят отражения в системе У, т.е. система У беденее подробностями, чем система Х

2. Ошибки в измерениях и передаче информации

Возникает вопрос, какое количество информации о системе Х дает наблюдения система У. Можно получить количественную оценку, как уменьшение энтропии системы Х, в результате получения сведений о системе У.

Можно доказать, что

Крайние случаи:

1. Полная независимость систем У и Х. Тогда Н(Х) = Н(Х|У) и I y->x. Т.е. если системы независимы, то количество информации будет равно нулю

2. Если состояние системы Х полностью определяется сосотоянием системы У и наоборот, то эти системы называются эквивалентными и в этом случаи Н(Х) = Н(У). Условная энтропия при этом равна нулю.

Энтропия непрерывной системы.

Ранее мы расматривали системы с дискретным множеством возможных состояний. Существует широкий класс систем, для который одни состояния плавно переходят в другие, т.е. количество возможных состояний бесконечно и можно говорить, что вероятность каждого отдельного состояния стремится к нулю, а вероятнгсть некоторого интервала состояний конечно и не равна нулю. Принято называть систему с множеством состояний дискретной, а систему с непрерывным множеством состояний непрерывной. Для непрерывных систем вводится понятие приведенной энтропии(Н*).

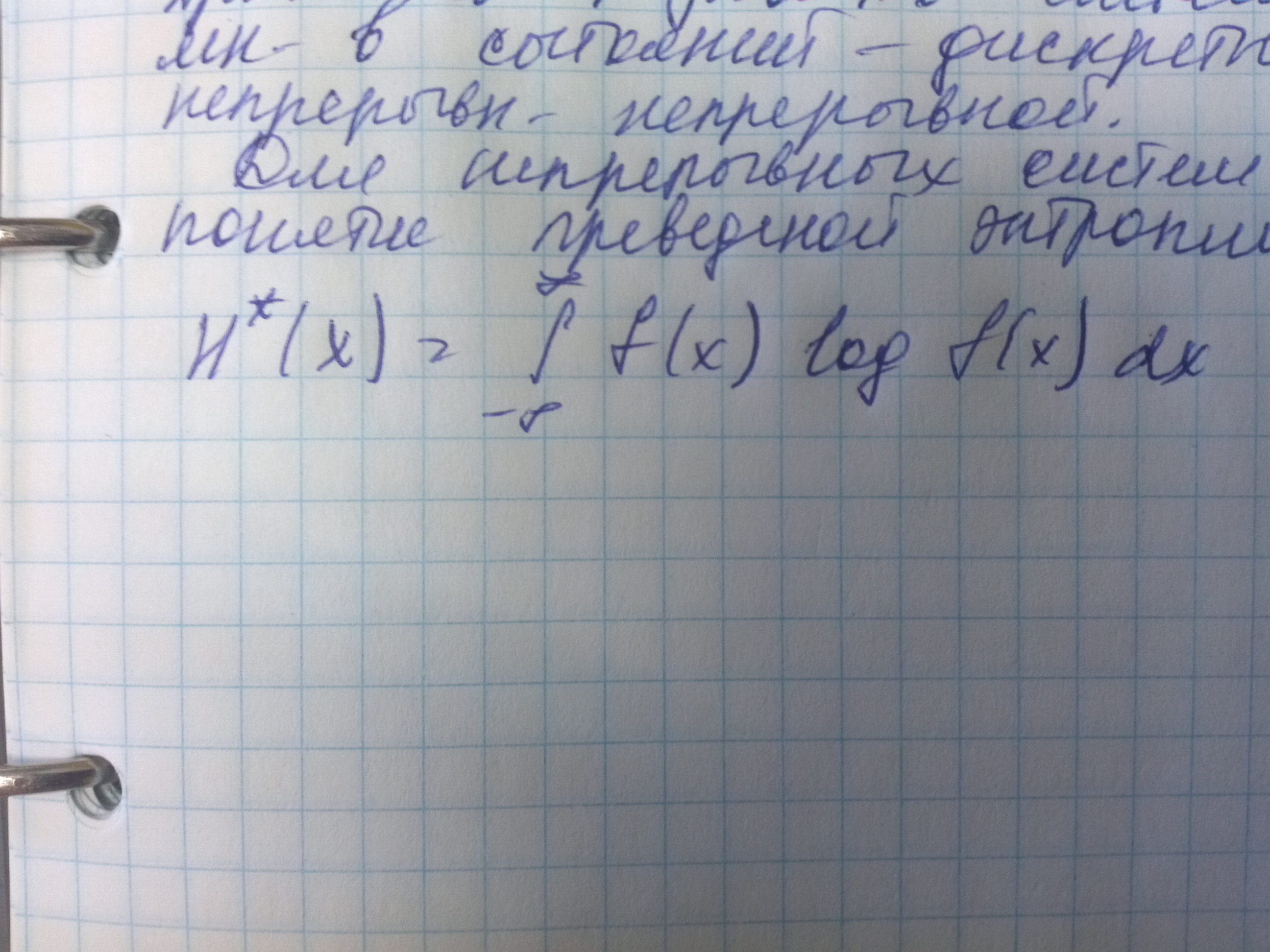
Если принимается некоторый интервал дельтаХ, например для прибора измеряющего непрерывную случайную величину, это может быть цена деления прибора, то соответствующая энтропия будет равна

По скольку логарифм дельтаХ при известном дельтаХ это константа, то назначение дельтаХ соответсвует назначению точки начала отсчета энтропии. Можно доказать, что все свойства и теоремы для энтропии дискретной системы, которые были ранее названы справедливы и для непрерывных систем. Можно также доказать, что энтропия непрерывной системы, все состояния которой принадлежат некоторому интервалу, от а до в, и эти состояния являются равновероятными, приведенная энтропия будет равна

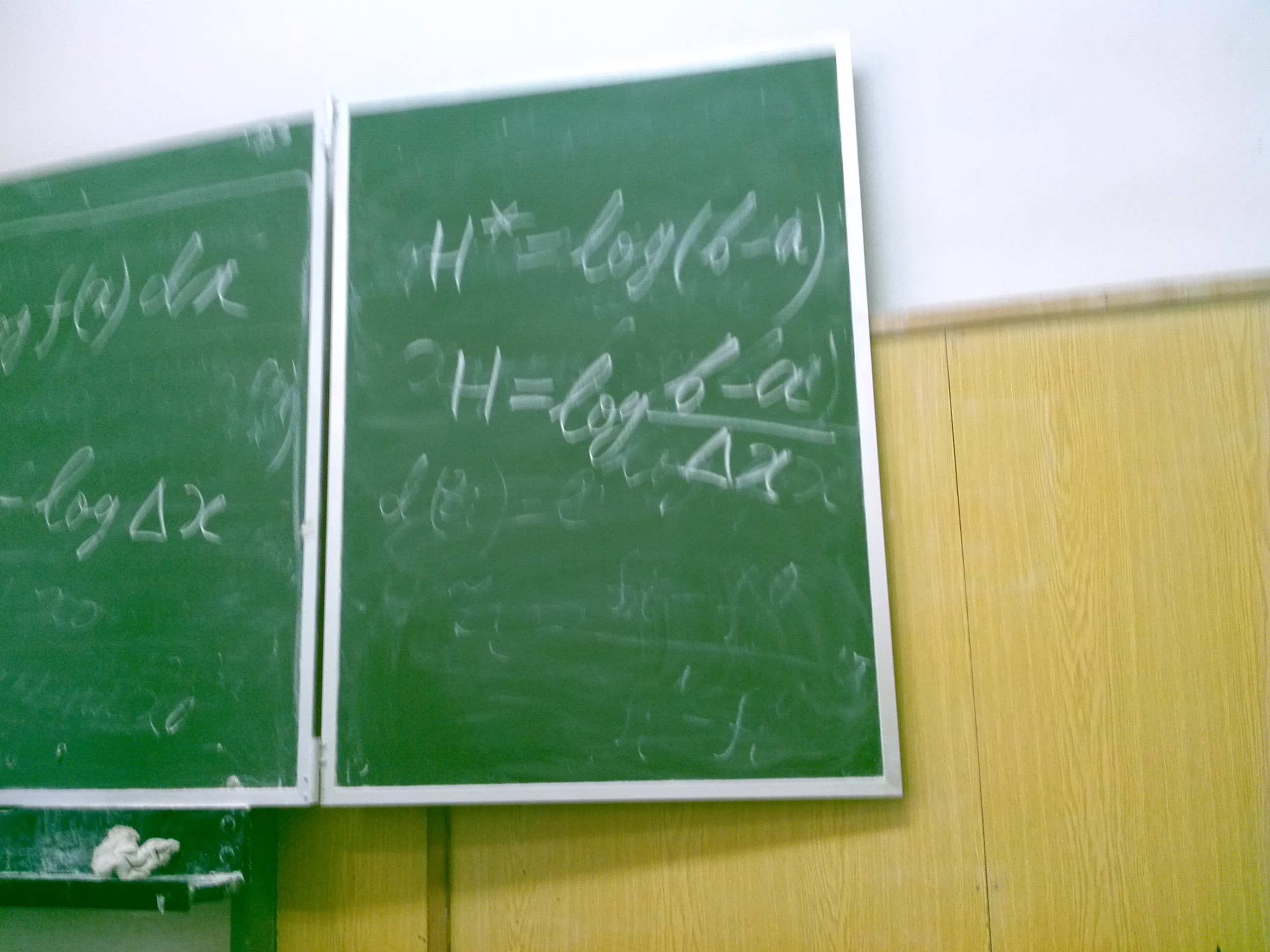
Теория кодирования информации

Кодирование называется отображение состояния одной физической системы с помощью состояний другой системы. Кодирование широко приминяется при передачи информации. Сам способ отображения при этом называется кодом. Существует много различных способов кодирования и есть общая теория, которая распространяется на любые способы, ее можно рассматривать, как применение теории информации к конкретной проблеме передачи информации от источника к приемнику. Пусть имеется некоторая система Х(например алфавит русского языка) и эта система может принимать случайным образом различные состояния х1,х2,хн. у1,у2,ум. Если м < н, то нельзя каждое состояние системы Х закодировать одним состоянием системы У. Тогда приходится использовать комбинации состояний системы У. Типичный пример азбука Морзе.

Самый простой способ кодирования состоит в том, чтобы пронумировать все буквы алфавита, а затем перевести номера в двоичную систему. Такой способ кодирвания приведет к значительному увеличению числа символов. Дело в том, что в текстах на естественном языке(русккий, английский) буквы встреыаются с разной частотой, а в данном простом способе кодирования это никак не учитывается. Для построения оптимального кода элементарные символы должны встречаться в среднем одинаково часто. Одним из экономичных способов построения кода для алфавита естественного языка являетсы код Шеннона - Фано. При построении кода Шеннона-Фано кодируемые символы или их комбинации разделяются на две равновероятные группы. Для тех групп которые попали в первую группу ставим 0, для другой 1. Оптимальный код обладает высокой чувствительностью к искажению информации при передачи данных по каналам связи. Эти искажения вызываются различными техническими причинами, которые обычно называют помехами. Для повышения устойчивости передачи информации применяется избыточная информация, т.е. некоторые служебные символы и т.п. для снижения чуствительности к искажениям. Рассмотрим систему Х - передатчик информации и систему У - приемник информации. Пусть известна производитльность источника информации, т.е. среднее количество двоичных единиц информации поступающее от источника в единицу времени. Произовдительность численно равна средней энтропии сообщения произовдимого источником в единицу времени Н1(Х). Пусть кроме того известна пропускная способность канала С1, т.е. максмальное количество информации(если передаются символы 0 и 1, то количество информации в битах), которое способен передать канал за туже единцу времени. Ставится вопрос,: какова должна быть пропускная способность, для того, чтобы канал справлялся со своей задаыей, чтобы информация от источника Х к приемнику У поступала без задержек. Ответ на этот вопрос дает перва теорема Шеннона С1>Н1(Х), т.е. всегда можно закодировать достаточно длинное сообщение таким образом, чтобы оно передавалось каналом связи без задержек, если пропускная способность канала больше чем производительность источника. Если же наоборот выполняется неравнество С1<Н1(Х), то передача информации без задержек не возможна.

Рассмотрим теперь ситуацию, кодгда передача информации по каналу связи мозет сопровоздаться искажениями в следствии помех. Для того чтобы исправить воздействие помех приходится использовать избыточную информацию, которую тоже передают по каналам связи. Можно показать, что мерой избыточности для исопользуемого языка может служить величина

причем эта средняя энтропия должна расчитываться для достаточно длинного фрагмента текста. М число применяемых символов. Любой ествественный язык обладает высокой степенью избыточности.

Рассмотрим далее перадачу по каналам связи информации в двоичной форме при возоможности искажения, т.е. когда двоичные символы могут ошибочно заменять друг друга. Если бы не было ошибок, то количество информации содержащееся в системе У относительно системе Х было бы равно энтропии системы Х. При наличии ошибок это количество информации будет меньше. Iy->x=H(X|Y), т.е. условная энтропия может рассмптриваться как потеря информации на один элементарный символ. При отсутствии помех пропускная способность канал будет равна C=k*log n, где к - число символов передаваемое в единицу времени, т.к. один символов может передавать самое большое log m информации. При наличии помех пропускная способность будет C=k*Iy<->xmax. В общем случаи определить Iy<->xmax очень сложно, но для некоторых простых частных случаев это удается. Рассмотрим следующий частный случай. Канал связи передает символы 0 и 1, к-символов в единицу времени. Каждый символ независимо от других может быть заменен на противоположный с веротяностью мю. Требуется найти пропускную спосбность канала С. Для такого частного случая можно оценить величину условной энтропии, которая будет равна

...

В соответсвии с вышеприведенной формулой при к =100 бит/ед.времени и мю=0,01 получим ню(мю)=0,0664

Ню(1-мю)=0,0144

С=~92 бит/ед.времени

Вторая теорема Шеннона

Пусть имеется источник информации Х, энтропия которого в единицу времени равна Н~(Х) и имеется канал с пропускной способностью С. Если выполняется неравенство Н~(Х)>С, то при любом кодировании передачи сообщения без задержек и искажений невозможно. Если выполняется противоположное неравенство Н~(Х)<С, то всегда можно закодировать достаточно длинное сообщение таким образом чтобы оно передавалось по каналам с отсутстсвием задержек и искажений с вероятностью сколь угодно близкой к единице.

Пример: Пусть имеется источник информации Х с энтропией в единицу времени Н~(Х)=100 бит, имеется два канал связи, каждый из которых может передавать в единицу времени 70 двоичных знаков, причем каждый двоичный знак может заменяться на противоположный с вероятностью 10%. Требуется выяснить достаточно ли пропускная способность этих двух каналов для передачи информации от источника.

Решение:

Ню(мю)+Ню(мю)=0,469

С=70*(1-0,469)=37,2

С~=2С=74,4

...(Система массового обслуживания с ожиданием). В зависимости от количества имеющихся каналов обслуживания различают одноканальные и многоканальные системы массового обсуживания.

Для систем массового обслуживания эффективность их работы можно оценивать по различным критериям связанным с прежде всего с их пропускной способностью, т.е. с количеством заявок, которые эта система может обслужить, задачи могут быть достаточно разнообразными, как и для систем вообще эти задачи можно разделить на задачи анализа и синтеза, например, задачи анализа являются определение средней длинны в очереди возникающей в системе с ожижанием при известных вероятностных харкатеристиках потокозаявок. К задачам синетза можно отнести, например, решение вопроса следует ли установить в магазине еще один кассовый аппарат.

Для систем массового обслуживания характерны задачи, которые можно отнести к задачам прогнозирования, например, определить как изменится нагрузка на сервер в единицу времени при увеличении числа клиентов к нему обращающихся и т.д. Для систем массового обслуживания практически во всех видах задач требуется устанавливать взаимозависимость между характеристиками потокозаявок, производительностью каналов обсуживания и эффективностью работы системы. Если бы заявки поступали бы в стого определенные заранее известные моменты времени, а характеристики производительности каналов обсуживания были бы заранее точно известны и оставались бы неизменными, то тогда эффективность систем массового обслуживания можно было бы точно определить заранее по достаточно простым детерменированным моделям. Однако для большинства практических задач связанных с системами массового обслуживания заранее не известно в какие именно моменты времени придут заявки и характеристики системы тоже известны не точно, а известны их средние значения и разброс вокруг этих средних значений. Для потока заявок обычно известны некоторые вероятностные характеристики. Поэтому эффективность работы системы оценивается тоже по вероятностным характеристикам, например, по вероятности того, что заявка останется не обслуженной, по средней длине очереди за какое то время. Все эти характеристики так или иначе связаны с пропускной способностью системы. В узком смысле под пропускной способностью обычно понимают среднее число заявок, которые могут быть обслуженны в ед.времени. Часто используют понятие относительной пропускной способности - отношение числа обслуженных заявок к числу поданных в среднем.

Поступающие в систему заявки образуют поток заявок и количество заявок изменяющееся во времени образуют случайный процесс. Для систем массового обслуживания чаще всего количество заявок образуют случайный процесс с счетым множеством состояний.

Рассмотрим систему Х с счетным множеством состояний xi. В любой момент времени t система Х может быть в одном из состояний входящих в множество возможных состояний. Обозначим Pk[t] вероятность того что в момент времени t система примет к-ое состояние. Для любого момента времени будет выполняться равенство E(от к=1 до n)Pk[t]=1. Совокупность вероятностей для каждого момента Pk[t] времени образует так называемое сечение случайного процесса. ...Бывают двух типов с дискретным временем и с непрерывным временем. Для процессов с дискретным временем система меняет состояние только в строго определенное, разделенное конечными интервалами моменты времени. Для случайных процессов с непрерывным временем переход к другому состоянию возможенным в любые моменты времени.

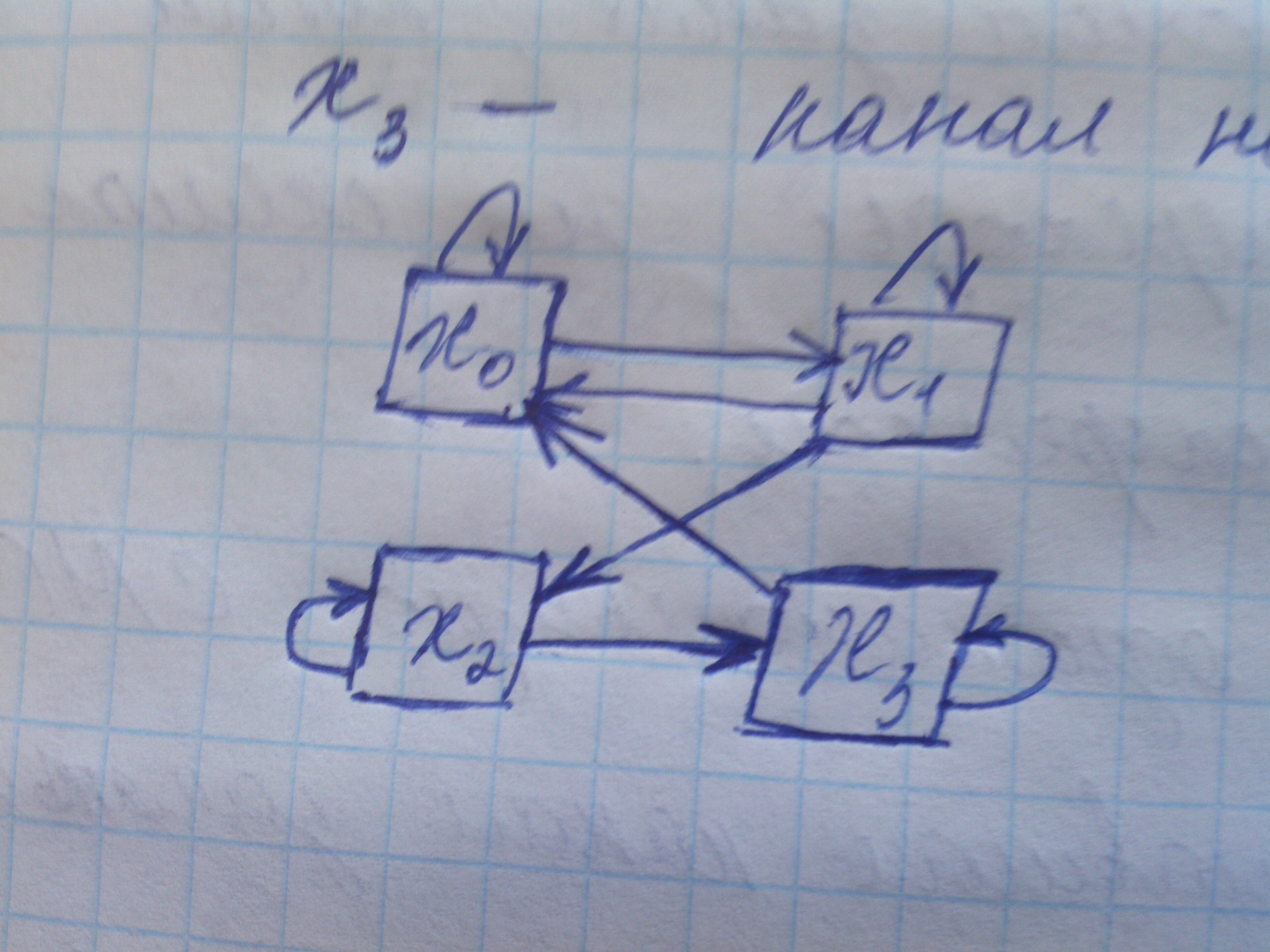
Рассмотрим далее систему состоящую из n самолетов, которые совершают бомбардировачный налет и при этом их может поражать ЗРК противника. На момент обнаружения группы самолетов заранее неизвестно какие из них будут сбиты. Если рассмотреть состояние системы, то получается следующая дискретное счетное множество возможных состояний x0 - состоянике когда ни один самолет не сбит,x1 -1, x2-2... xn - сбиты все. Можно изобразить схему переходов системы от состояния к состоянию следующим образом:

...В данном случаи это означает что вероятность сбивания двух и более самолетов стремится к нулю, т.е. рассматриваются достаточно близкие моменты времени или рассматриваются только события, заключающиеся в сбивании одного самолета.

На практике часто встречаются системы в которых возможны обратимые переходы, например, телефонный канал был свободен, заняли, освободили. Такие переходы на схемах показывают двусторонними стрелками.

Рассмотрим одноканальную систему массового обслуживания в которой заявка заставшая канал занятым не становится в очередь, а покидает систему. Такая система называется система массового обслуживания с отказами. Типичный пример телефонный канал. Для такой системы возможны два состояния x0 -канал свободен и x1 - канал занят.

Для n канальной системы такого же типа, n телефонных каналов, расмотрим состояние, в которых может оказаться система. Рассмотрим теперь систему, в которой возможны следующие 4 состояния при одном канале: х0 - канал исправен и свободен, х1 канал исправен и занят, х2 канал неисправен и ждет ремонта, х3 канал неисправен и ремонтируется.

Потоки событий их виды и свойства

Под потоком событий понимается последовательность событий, происходящих одно за другим в конкретные промежутки времени. Если речь идет об одинаковых событиях(например событие заключается в обращении к серверу и все обращения считаются одинаковыми), то такие потоки событий называются однородными. Потоки событий рассматриваются на временной прямой.

Имеется различные классификации потоков событий. Теория систем массового обслуживания и в других разделах в которых речь идет о потоках событий рассматриваются различные виды потоков, среди которых особенно часто выделяются следующие:

• Регулярный поток. Поток называется регулярным, если события следуют друг за другом через строго определенные промежутки времени.

• Стационарные потоки. В стационарных потоках вероятность поподания того или иного числа событий на промежуток времени длинной t не зависит от того в каком месте на оси времени находтся этот промежуток, а зависит только от длинны промежутка.

• Поток называется ординарным, если вероятность попадания двух или более событий на рассматриваемый элементарный промежуток времени Δt пренебрежимо мала по сравнению с вероятностью попадания на этот промежуток одного события. Пример - звонки по телефону.

• Поток событий называется потоком безпоследействия, если для любых неперекрывающихся промежутков времени число событий попадающих на один из промежутков не зависит от числа событий попадающих на другой промежуток.

Роль простейшего потока похожа на роль нормального распределения в математической статистике. Подобно тому, как сумма случайных величин как правило имеет нормальное распределение, так и сумма потоков событий как правило стремится к простейшему потоку. Подобно тому как к нормальному распределению разработана полная теория статистического оценивания, так и для простейших потоков событий наиболее полно по сравнению с другими потоками постороен математический аппарат.

Можно доказать, что простейший поток имеет статистическое распределение, которое называется статистическое распределение Пуассона.

Тау длинна произвольного промежутка времени, лямба плотность потока событий, т.е. среднее число событий происходящее на единицу времени.

Рм(т) - вероятность того, что за время тау произойдет ровно м событий. В соответсвии с распределением Пуассона вероятность того что за рассматриваемый промежуток времени тау не произойдет ни одного события будет равна. Простейший поток событий часто называют также Пуассоновским потоком. Можно доказать, что если поток событий имеет распределение пуассона, то такой поток является простейшим.

Можно найти плотность распределения для промежутка времени между событиями при простейшем потоке.

Показательный закон распределения имеет только один параметр - лямбда, т.е. и функция распределения и плотность распределения зависит только от параметра лямбда. Если рассмотреть математическое ожидание длинны промежутка времени между событиями то можно получить mt=1/лямбда. Для дисперсии можно получить выражение Dt=1/лямбда^2. Gt=1/лямбда.

Нестационарный Пуассоновский поток

Рассмотрим поток событий, обладающий свойсвами ординарности и отсуствия последействия и необладающий свойсвом стационарности. Такой поток не является простейшим, но его удобно рассматривать как простейший поток с изменяющимися во времени параметрами, т.е. для простоейшего потока все статистические характеристики не изменяются во времени, а для потока, который принято называть нестационарный пуассоновский поток статистические характеристики изменяются. В какой то определенный момент времен эти характеристики принимают определенные значения, которые называют мгновенными значениями. Вводится понятие мгновенной плотности потока(лямбда от т). Если для простейшего потока лямбда - константа, то для нестационарного пуассоновского потока лямбда от т - это функция времени. Если рассмотреть некоторый момент времени т и некоторый следующий промежуток времени Δт, причем принять этот промежуток достаточно малым, среденяя плотность потока на этом промежутке может быть определена таким образом

Где м это число событий произошедших к рассматриваемому моменту времени. Если сделать предельный переход, т.е. рассмотреть

То этот предел будет равен мгновенной плотности потока. Очевидно что лямбда от т является первой производной от функции м(т).

Также как и для простейшего потока можно доказать, что число событий попадающих на промежуток времени длинны тау, начинающийся в момент т0 будет распределенно по закону пуассона. Получим

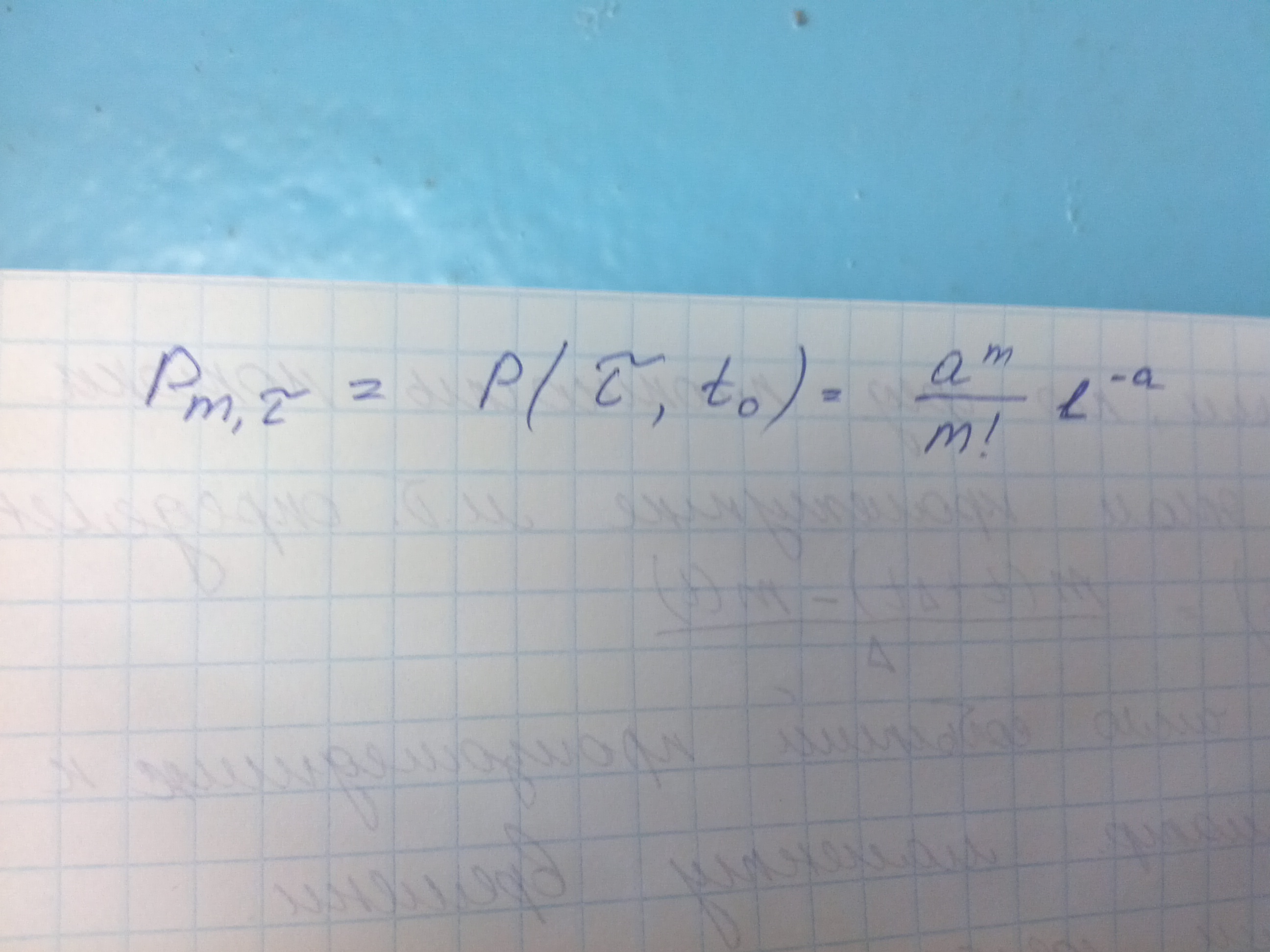
Здесь а - математическое ожидание числа событий на промежутке времени от т0 до т0 + тау. Если выразить его через плотность потока лямбда, то получим

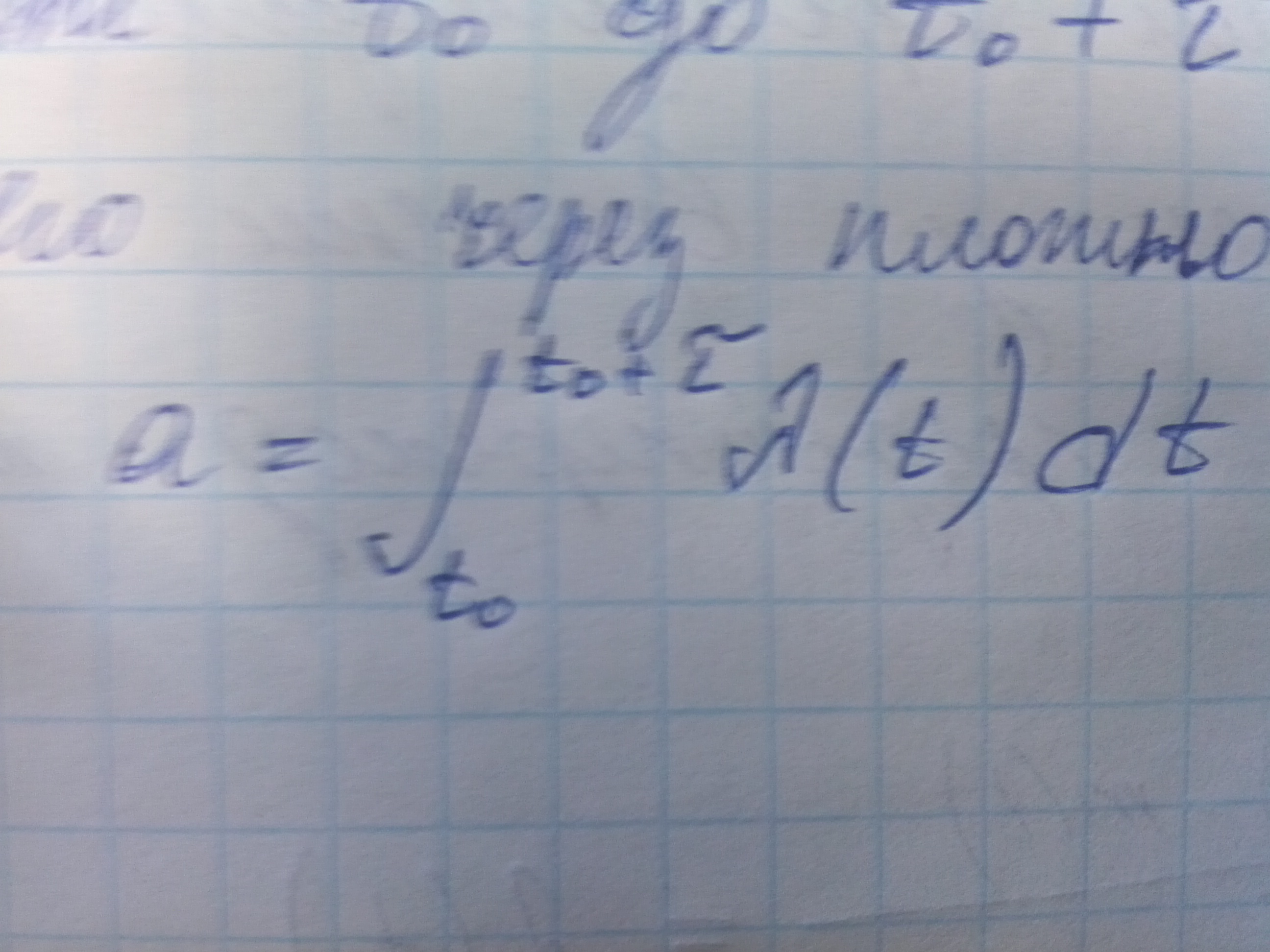
Отсюда видно что а зависит как от плоности потока и длинны промежутка, так и от расположения этого промежутка на оси времени, т.е. зависит от т0. Найдем теперь для такого потока распределение промежутка времени. Можно получить функцию распределения в виде

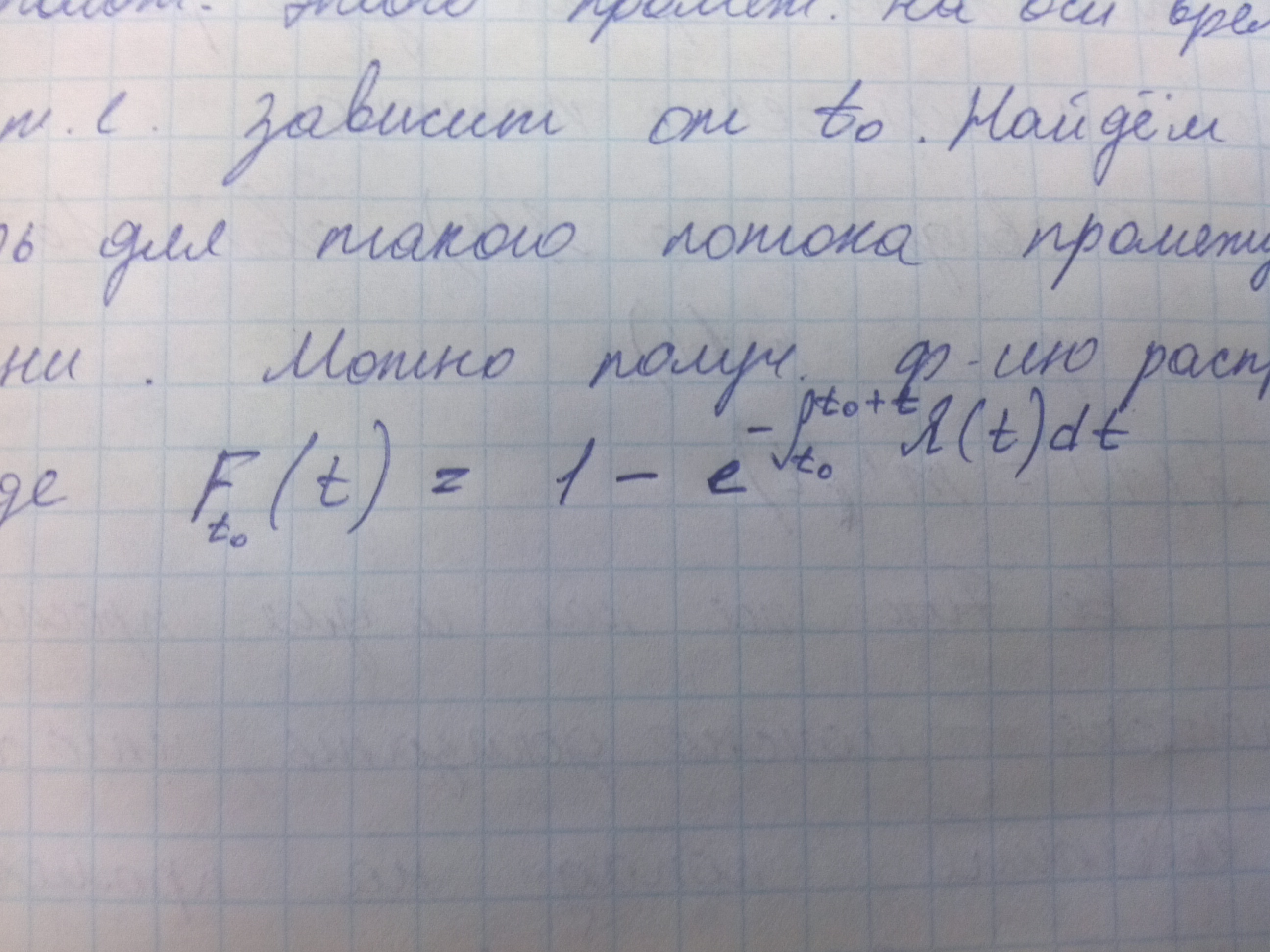
Такой закон распределения не является показательным. Для конкретных частных случаев функции лямбда от т иногда удается получить достаточно простую функцию распределения, например, если лямбда от т линейная функция времени. В общем случаи функция распределения может быть достаточно сложной. Таким образом работать с нестацитнарным пуассоновским потоком значительно сложнее чем с простейшим, хотя то что сохраняется отсуствие свойства последействия значительно облегчает решение задач по сравнению с потоками в которых это свойство не выполняется, поэтому на практике моделирование систем массового обслуживания с помощью нестационарного пуассоновского потока распространено достаточно широко.

Потоки с ограниченным последействием(потоки Пальма)

Если нестационарный пуассоновский поток является обобщением простейшего потока по свойству стационарности, то потоки Пальма является обобщением простейшего потока по свойству последействия. Рассмотрим ординарный однородный поток событий. Он является потоком с ограниченным последействием(потоком Пальма), если промежутки времени между последовательными событиями являются независимыми случайными величинами. Очевидно что простейший поток можно рассматривать как частный случай потока Пальма, но в простейшем потоке промежутки времени между событиями имеют показательное распределение. Для потока Пальма это не обязательно. Потоки пальма часто встречаются на практике как выходные потоки для систем массового обслуживания, например, под определение потока Пальма подоходит поток событий, который образует заменяемые в процессе ремонта детали технической системы. Имеется теорема пальма, которая характеризуе появление на практике потоков пальма:

Пусть на систему массового обслуживания поступает поток заявок который удовлетворяет свойства потока Пальма, причем заявка заставшая все каналы занятами получает отказ, т.е. не обслуживается. Если при этом время обслуживания имеет показательный закон распределения, то поток необслуженных заявок также является потоком Пальма. В частности если входной поток заявок будет простейшим, то выходной поток необслуженных заявок уже не будет простейшим, но при этом он будет потоком Пальма.