Билет № 11. Тройной интеграл. Его свойства и применение. Примеры.

Пусть в пространстве задана некоторая плоскость V и ограничена поверхностью S.

Пусть дана V и на её границы определена f(x,y,z) ≥ 0, разобьём V произвольным образом на Δ υ_i , где Δ υ_i обозначает не только саму подобласть, но и её объём. В каждой подобласти Δ υ_i выберем произвольным образом P_i и обозначим через f(P_i) значения функции в этой точке. Составим

_iΣ f(P_i) Δ υ_i (1)

и будем неограниченно увеличивать число Δ υ_i, так чтобы max (diam Δ υ_i) → 0. Если f непрерывна, то предел интегрирования сумм вида (1) будет существовать. Этот предел не зависящий не от способа разделения υ, ни от выбора точек (P_i) обозначается символом _V∫∫∫ f(P) dυ и называется тройным интегралом.

_{max(diam Δ υi)→ 0}lim _iΣ f(P_i) Δ υ_i = _V∫∫∫ f(P) dυ= _V∫∫∫ f(x,y,z) dxdydz (2)

Если f считать обьёмной плотностью распределения некоторого вещества в области V, то (2) даёт массу всего всего вещества, заключенного в объёме V.

Введем понятие правильной (двумерной) области.

П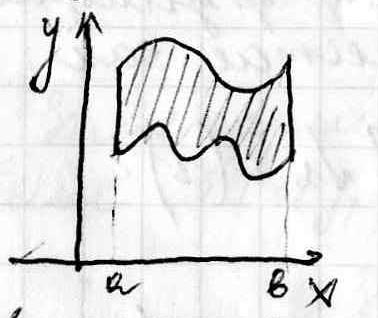 усть область ограничена линиями y=y₁(x), y=y₂(x), x=a, x=b. Причем y₁(x) ≤ y₂(x), а≤х≤b. И эти функции являются непрерывными на данном отрезке. Такую область называют правильной в направлении оси у.

Аналогично определяется область правильная направлению оси х. Область правильная, как в направлении оси х, так и в направлении оси у называется правильной двумерной областью.

Пусть область V обладает следующими свойствами.

1. Всякая прямая, проведенная через внутреннюю точку области V пересекает поверхность S в двух точках.

2. Вся область проектируется на плоскость Oxy в правильную двухмерную область D.

3. Всякая часть области V, отсеченная плоскостью, параллельной любой зи неординатных плоскостей также обладает свойствами (1) и (2).

О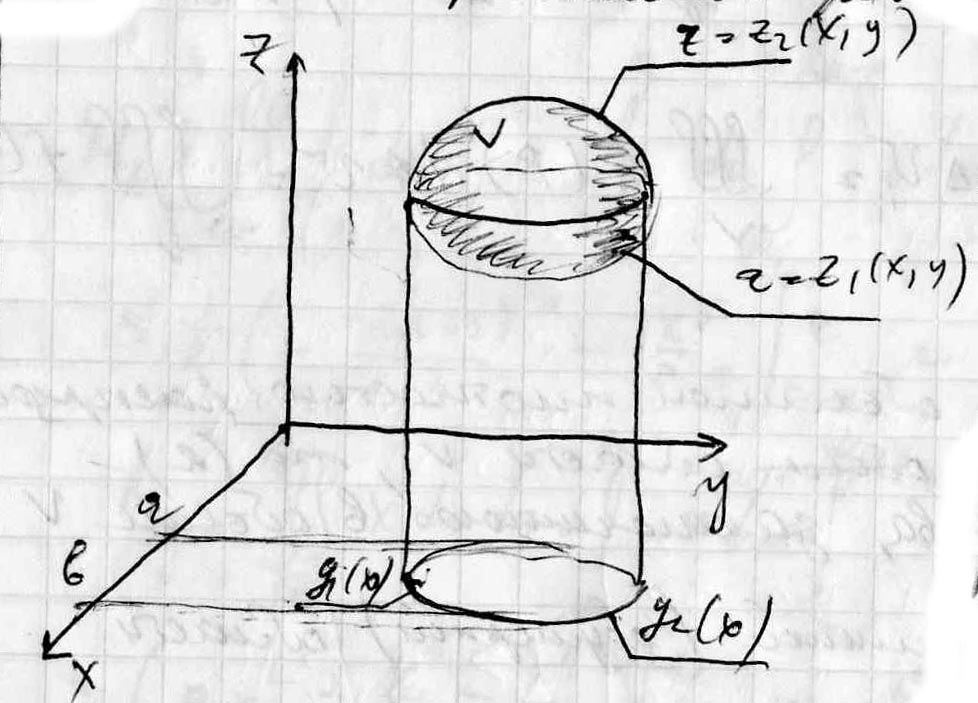 бласть V обладающую свойствами 1-3 называют трехмерной областью.

Пусть поверхность, ограничивающая V снизу имеет уравнения z=z₁(x,y), а поверхность, ограничивающая z сверху z=z₂(x,y).

Введем понятие трехкратного интеграла и I_v по области (V) от функции f(x,y,z) определенной и непрерывной в области V.

Предположим, что область D ограничена линиями y=y₁(x), y=y₂(x), x=a, x=b. Тогда трехкратный интеграл от функции f(x,y,z) по области V определяется так:

I_v=_a^b∫ (_y1(x,y)^y2(x,y)∫[ _z1(x,y)^z2(x,y)∫ f(x,y,z)dz]dy)dx (3)

Заметим, что в результате интегрирования по z и подстановки пределов во внешних скобках получается функция от ху. Далее вычисляется двойной интеграл от этой функции по D, как было рассмотрено выше.

Свойства тройного интеграла.

1. При любом разбиении области V на конечное число областей V₁, V₂, …, V_n плоскостями, параллельным координатным плоскостям имеет место равенство I_V= I_V1+I_V2+…+ I_Vn (4)

2. Если m и М соответственно наименьшее и наибольшее значения функции f(x,y,z) то имеет место неравенство

m_v ≤ I_V ≤ M_v , где V – объём области

3. Трехкратный интеграл I_V от непрерывной функции f(x,y,z) по области V равен произведению его объёма V на значение функции в некоторой функции в некоторой точке P* области V:

I_V=f (P*)V (6)

Теорема.

Тройной интеграл от функции f(x,y,z) по правильной области V равен трехкратному интегралу по той же области

_V∫∫∫ f(x,y,z) dυ =_a^b∫ (_y1(x,y)^y2(x,y)∫[ _z1(x,y)^z2(x,y)∫ f(x,y,z)dz]dy)dx (7)