Уравнение затухающих колебаний. Амплитуда, частота, коэффициент затухания.

Уравнение затухающих колебаний представим в видегде- тормозящая сила (трение), пропорциональная скорости. Решения этого уравнения ищем в виде. Подставим вид решения в уравнение- характеристическое уравнение, позволяющее найти неизвестную константу.

Если , то возникают колебания, т.е.

Решение уравнения представим в виде

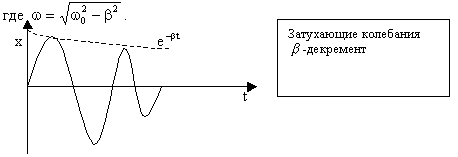
Логарифмический декремент затухания, время релаксации, добротность колебательной системы.

Логарифмический декремент затухания– натуральный логарифм отношения двух амплитуд, соответствующих моментам времени, отличающихся на период.

Время релаксации– промежуток времени в течении которого амплитуда колебаний уменьшиться вeраз.

, гдеNe– число колебаний, соверщённых за время, когда амплитуда колебаний уменьшается в е раз.

Добротность колебательной системы

Вынужденные колебания.

Вынужденные колебания- это колебания, происходящие под действием периодического внешнего воздействия.

Н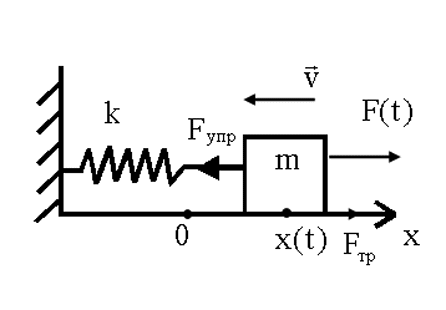а грузmдействует внешняя сила, изменяющаяся по гармоническому закону

Получим дифференциальные уравнения:

Приведем уравнения к каноническому виду - делим на коэффициент при старшей производной и переносим все члены уравнения, содержащие неизвестную функцию, в левую часть:

Введём обозначения

.

Явление механического резонанса.

См. Резонанс

Резонансная частота.

См. Резонанс

Резонанс.

.

Таким образом, амплитуда вынужденных колебаний изменяется с изменением частоты внешнего воздействия. При определенной частоте амплитуда достигает максимума. Это явление называется резонансом, а соответствующая частота - ω_рез- резонансной. Для определения ω_резисследуем функцию A(ω) на максимум, для этого достаточно найти минимум знаменателя у выражения A(ω) .

.

При 2β²> ω²₀резонанс отсутствует ( ω_рез- мнимое число).

Амплитуда при резонансе получается при подстановке найденного выражения ω_резв формулу для A(ω).

.

При β << ω₀:

.

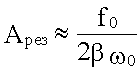При ω = 0 отклонение системы от положения равновесия

.

График зависимости A(ω) при различных β носят название резонансных кривых.

Волны в упругой среде.

Упругая среда-среда непрерывно распределенная в пространстве и обладающая упругими свойствами.

Волны-возмущения, распространяющиеся в среде или в вакууме и несущие с собой энергию. При распространении волны происходит перенос энергии волной без пререноса вещества, т.е. при распространении волны частицы колеблются возле своих равновесных положений, т.е. вместе с волной от частицы к частице передается колебательное состояние и его энергия.

Уравнение плоской бегущей волны.

Гармоническая бегущая волна является плоской волной, т.к. ее волновые поверхности

(ω(t-)+φ₀)=const представляет собой совокупности плоскостей, параллельных друг другу и перпендикулярных оси х.

S(0)=A₀cos(ωt+φ₀)

1).S(x)=A₀cos(ω(t-r)+φ₀)=A₀cos(ω(t-)+φ₀)-распространение волны вдоль положительного направления оси х.

(ω(t-)+φ₀)=const

dt==0,=-фазовая скорость.

2). S(x)=A₀cos(ω(t+r)+φ₀)=A₀cos(ω(t-)+φ₀)

………………………………………………………………………………………

к=- волновое число

S(x)=A₀cos(ω(t-r)+φ₀)=A₀cos(ω(t-)+φ₀)= A0cos(ωt-)+φ₀)=A0cos(ωt- kх+φ₀)

Если имеется среда, ……………………………………, то: S(х)=A₀cos(ωt-kх+φ₀), А-амплитуда плоскости х=0,

S(х)=A₀cos(ωt-+φ₀),- скалярное произведение волнового вектораи радиус-вектора.