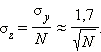Пример 3
Найти распределение вероятности числа очков, выпавших на кубике с первого броска, медиану, математическое ожидание, дисперсию и среднеквадратичное отклонение.
Решение
Выпадение любой грани равновероятно, так что распределение будет выглядеть так:
Математическое ожидание Mx = 3,5 (см. пример в начале параграфа). С вероятностью 1/2 случайная величина x ≤ 3. С такой же вероятностью x ≥ 4. Таким образом, медианой случайной величины является любое число из интервала (3; 4). Обычно в качестве медианы указывают среднее значение из этого интервала: x1/2 = 3,5. В нашем случае медиана совпала с математическим ожиданием, в других распределениях это не так. Дисперсия:
Среднеквадратичное
отклонение |
Свойства математического ожидания
|
Пример 4
Найти математическое ожидание суммы и произведения очков, выпавшей на двух кубиках.
Решение
В примере 3 мы нашли, что для одного кубика M (x) = 3,5. Значит, для двух кубиков
|
Свойства дисперсии
|
Пример 5
Найти математическое ожидание и дисперсию суммы очков, выпавших при бросании кубика N раз.
Решение
Случайный процесс можно представить как сумму единичных бросков. Для единичного броска
Пусть за N бросков на кубике выпало y очков. Тогда
Если z –
среднее количество очков, выпавших
на кубике за N бросков:
Этот
результат верен не только для бросков
кубика. Он во многих случаях определяет
точность измерения математического
ожидания опытным путем. Видно, что при
увеличении количества измерений Nразброс
значений вокруг среднего, то есть
среднеквадратичное отклонение,
уменьшается пропорционально |
Дисперсия случайной величины связана с математическим ожиданием квадрата этой случайной величины следующим соотношением:
|

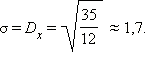 Видно,
что отклонение величины от среднего
значения очень велико.
Видно,
что отклонение величины от среднего
значения очень велико.