7. Плотность вероятности. Нормальный закон распределения. Математическое ожидание и дисперсия. Графическое представление. Примеры

Случайная величина называется непрерывной, если множество ее возможных значений представляет собой некоторый конечный или бесконечный промежуток числовой оси.

Случайная величина называется дискретной, если совокупность всех ее возможных значений представляет собой конечное или бесконечное, но обязательно счетное множество значений, т.е. такое множество, все элементы которого могут быть пронумерованы и вписаны в соответствующей последовательности.

Пло́тность вероя́тности — один из способов задания вероятностной меры на евклидовом пространстве  . В случае когда вероятностная мера является распределением случайной величины, говорят о плотностислучайной величины.

Пусть   является вероятностной мерой на  , то есть определено вероятностное пространство  , где   обозначает борелевскую σ-алгебру на  . Пусть m обозначает меру Лебега на  .

Определение 1. Вероятность   называется абсолютно непрерывной (относительно меры Лебега) ( ), если любое борелевское множество нулевой меры Лебега также имеет вероятность ноль:

Если вероятность   абсолютно непрерывна, то согласно теореме Радона-Никодима существует неотрицательная борелевская функция   такая, что

,

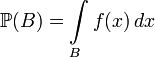где использовано общепринятое сокращение  , и интеграл понимается в смысле Лебега.

Определение 2. В более общем виде, пусть   — произвольное измеримое пространство, а μ и ν — две меры на этом пространстве. Если найдется неотрицательна f, позволяющая выразить меру ν через меру μ в виде

ν(A) =	∫	fdμ,
	A

то такую функцию называют плотностью меры ν по мере μ, или производной Радона-Никодима меры ν относительно меры μ, и обозначают

.

[Свойства плотности вероятности

• Плотность вероятности определена почти всюду. Если f является плотностью вероятности   и f(x) = g(x) почти всюду относительно меры Лебега, то и функция g также является плотностью вероятности  .

• Интеграл от плотности по всему пространству равен единице:

.

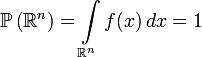Обратно, если f(x) — неотрицательная п.в. функция, такая что  , то существует абсолютно непрерывная вероятностная мера   на   такая, что f(x) является её плотностью.

• Замена меры в интеграле Лебега:

,

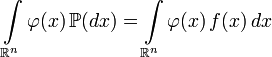где   любая борелевская функция, интегрируемая относительно вероятностной меры  .

Плотность случайной величины

Пусть определено произвольное вероятностное пространство  , и   случайная величина (или случайный вектор). X индуцирует вероятностную меру   на  , называемую распределением случайной величины X.

Определение 3. Если распределение   абсолютно непрерывно относительно меры Лебега, то его плотность   называется плотностью случайной величины X. Сама случайная величина X называется абсолютно непрерывной.

Таким образом для абсолютно непрерывной случайной величины имеем:

.

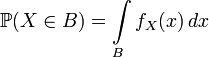Определение. Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности

Нормальный закон распределения также называется законом Гаусса.

            Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.

Можно легко показать, что параметры  и , входящие в плотность распределения являются соответственно математическим ожиданием и средним квадратическим отклонением случайной величины Х.