19. Основные (первичные) понятия теории вероятности, используемые для анализа точности обработки и контроля

Случайное событие — событие, которое при наличии сово­купности условий F может либо произойти, либо не произойти. Достоверное событие — событие, которое обязательно произой­дет при наличии условий F. Вероятностью события А называют отношение числа благоприятствующих ему случаев (исходов) т к общему числу исключающих друг друга случаев п: Р(А) == т/п. Вероятность достоверного события равна единице, невозможного

события — нулю, а случайного события — числу, заключенному между нулем и единицей (0 < Р(А) < 1). Таким образом, для про­извольного случайного события справедливо неравенство 0£Р(А)£1. Случайная величина Х — величина, наблюдаемое значение которой зависит от случайных причин и поэтому на­перед неизвестно. Случайные величины могут быть дискретными (например, число бракованных деталей в партии и др.) или не­прерывными (например, отклонение размера детали от номинала, высота микропрофиля в данной точке и др.). Полный набор всех возможных значений случайной величины Х называется генеральной совокупностью.

Закон распределения случайной величины Х — всякое соот­ношение, устанавливающее связь между возможными значения­ми x_i случайиой величины Х и соответствующими им вероят­ностями p_i . Его можно задать таблично, аналитически (форму­лами) или графически. В наиболее обобщенной форме закон распределения описывается с помощью интегральной функции распределения или дифференциальной функцией распределения.

20. Интегральная функция распределения

Функция распределе­ния F(x) — это функция, определяющая вероятность того, что случайная величина Х примет значение меньше данного значе­ния x: F(x)=P(X<x). Из определения следует, что 0£F(x)£1, причем F(-оo)=0 и F(+oo)=l. Вероятность того, что значение случайной функции попадет в интервал (a, b), равна разности значений интегральной функции на концах интервала:

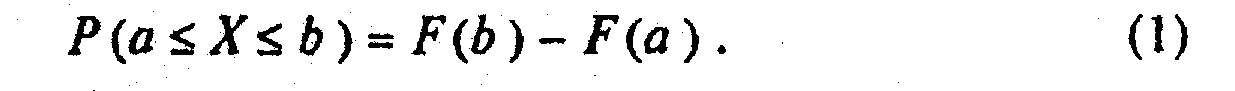
21. Дифференциальная функция распределения

Плотность веро­ятности f(x) — это первая производная от функции распреде­ления. График функции f(x) называют кривой распределения. Вероятность попадания Х в заданный интервал (a, b) равна

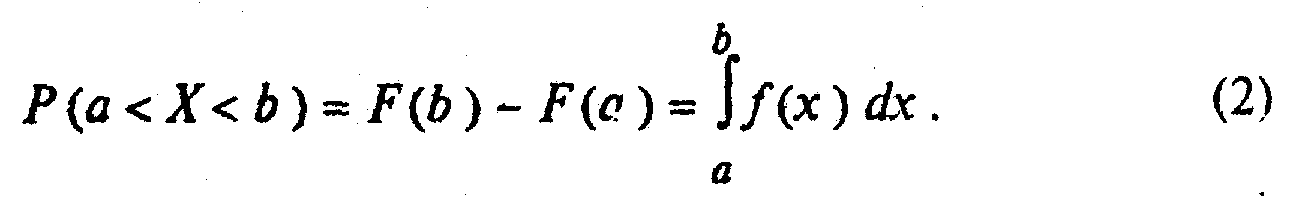
Геометрически эта вероятность равна площади криволиней­ной трапеции, ограниченной осью абсцисс, прямыми х = а и х == b и кривой распределения (рис. 1, а). Площадь под всей кривой равна единице.

22. Характеристики случайных величин.

Числовые ха­рактеристики случайных величин делят на 3 группы: а) харак­теристики положения случайной величины на числовой оси (ма­тематическое ожидание, мода, медиана); б) характеристики рас-

сеяния вокруг некоторого центра группирования (дисперсия, среднее квадратическое отклонение); в) моменты (начальные и центральные).

Математическое ожидание М(Х) (или т_x) — это среднее значение случайной величины Х из генеральной совокупности:

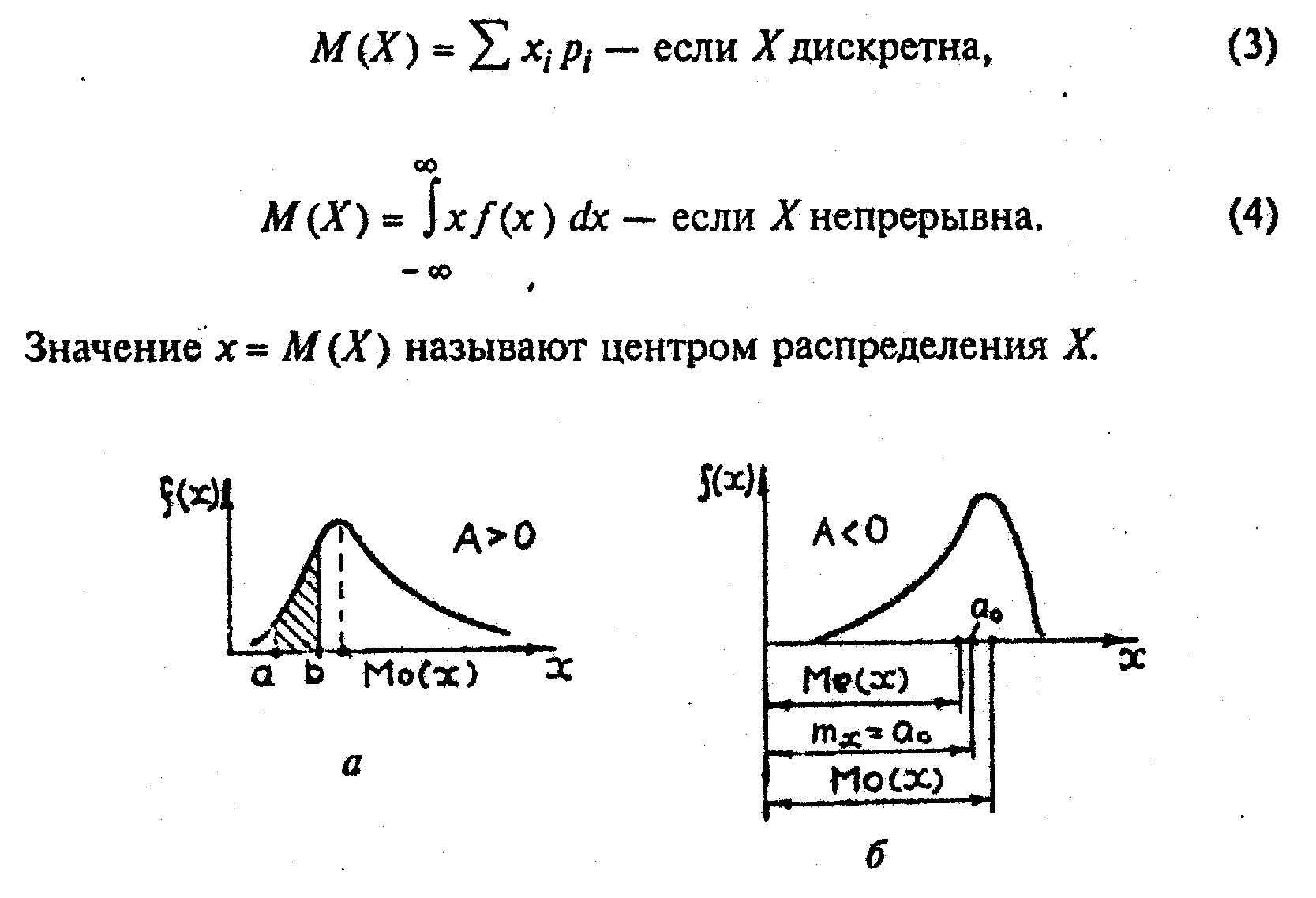
Рис. 1. Показатели несимметричности кривых распределения:

а — положительная ассиметрия; б — отрицательная ассиметрия

Мода Мо (X) — это значение Х_i с наибольшей вероятностью (или плотностью вероятности). Медиана Me (X) — значение Хёнёi, при котором площадь под кривой распределения делится пополам. В общем случае значения М(Х), Мо(Х), Me (X) могут не совпадать (рис. 1, б).

Дисперсия D (X) случайной величины X— это математическое ожидание квадрата отклонения случайной величины от ее ма­тематического ожидания:

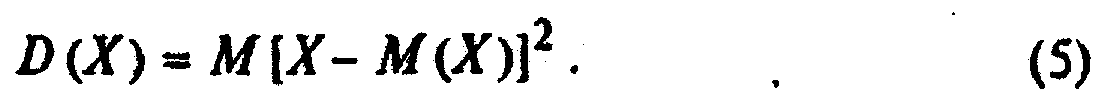
Среднее квадратическое отклонение s_x — это корень квадратный из дисперсии (является моментом второго порядка).

Моменты больших порядков используют для описания формы кривой распределения. Так, третий центральный момент (^3)

применяют для оценки ассиметрии (скошенности) кривой распределения относительно математического ожидания, вычисляя с его помощью коэффициент ассиметрии А:

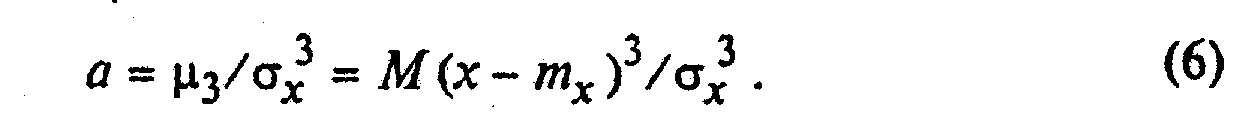
Если мода Мо(Х) находится слева от среднего значения т_x, то ассиметрия положительна. Если мода расположена справа от среднего значения,, то ассиметрия отрицательна (см. рис. 1). Четвертый центральный момент (m₄) характеризует "остроту" вершины кривой распределения. Для этого вычисляют коэффициент эксцесса Е:

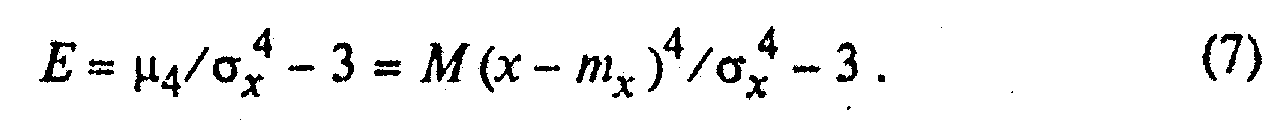
Эксцесс положителен для островершинных кривых распре­деления и отрицателен для плосковершинных. Для закона Гаусса Е=0.