2. Дробно – линейная подстановка

Интегралы типа , где 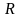– рациональная функция, a, b, c, d – действительные числа, – натуральные числа.

Интегралы такого вида вычисляются с помощью подстановки

,

где n – общий знаменатель дробей (наименьшее общее кратное чисел ). В результате этой подстановки подынтегральная функция преобразуется в рациональную.

Пример 3. Вычислить .

Решение: Положим ; тогда и

3. Интегрирование дифференциального бинома

Интегралы типа , где a, b – действительные числа, m, n, p – рациональные числа.

Подынтегральное выражение называют дифференциальным биномом.

Данный интеграл выражается в конечном виде (т.е. первообразная представляет собой элементарную функцию) лишь в следующих трех случаях (этот результат получен выдающимся русским математиком и механиком Пафнутием Львовичем Чебышёвым (1821 – 1894):

1. если p – целое число, то применяется подстановка , где k – наименьшее общее кратное знаменателей дробей m и n;

2. если – целое число. Тогда применяется подстановка , где – знаменатель дроби ;

3. если – целое число. В этом случае используется подстановка , где – знаменатель дроби p.

Пример 4. Вычислить .

Решение: Перепишем исходный интеграл .

Это интеграл от дифференциального бинома, где ; . Следовательно, имеет место случай 2) интегрируемости.

Подстановка дает: .

Поэтому, ,

где .

4. Тригонометрическая подстановка

Интегралы типа , , приводятся к интегралам от функций, рационально зависящих от тригонометрических функций, с помощью тригонометрических подстановок: для первого интеграла; для второго интеграла; для третьего интеграла.

5. Интегралы типа , где – рациональная функция относительно x и .

Один из возможных методов интегрирования состоит в следующем.

Выделяем полный квадрат в квадратном трехчлене 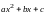и совершаем замену переменной по формуле , после этого исходный интеграл сводится к одному из следующих трех типов:

1. ;

2. ;

3. .

Эти три типа интегралов вычисляются с помощью тригонометрической подстановки соответственно.

1. ,

2. ,

3. .

В результате этих подстановок указанные интегралы приводятся к виду или .

В частном случае, когда требуется вычислить интегралы типа и , можно обойтись без замены переменной. Вычислим первый из них:

.

Для вычисления последнего интеграла воспользуемся методом интегрирования по частям: .

Тогда .

Вернемся к исходному интегралу: .

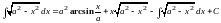Из последнего равенства получаем , и, разделив обе части на два, найдем .

Поступая аналогично для , получим .

Замечание. Интеграл типа целесообразно находить с помощью подстановки .

17