
- •Неопределенный интеграл Понятие неопределенного интеграла
- •Свойства неопределенного интеграла
- •Основные методы интегрирования
- •Метод непосредственного интегрирования
- •Метод интегрирования способом подстановки (замены переменой)
- •Метод интегрирования по частям
- •Интегрирование тригонометрических функций.
- •Универсальная тригонометрическая подстановка
- •Интегралы типа , .
- •Использование тригонометрических преобразований
- •Интегрирование иррациональных функций.
- •Квадратичные иррациональности
- •Дробно – линейная подстановка
- •Интегрирование дифференциального бинома
- •Тригонометрическая подстановка
Основные методы интегрирования
Метод непосредственного интегрирования
Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.
При сведении данного интеграла к табличному часто используются следующие преобразования дифференциала (операция «подведения под знак дифференциала»).
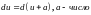
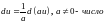
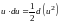
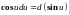
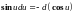
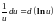
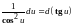
Пример 1.
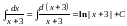 .
.
Пример 2.
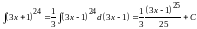
Пример 3.
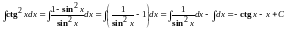 .
.
Метод интегрирования способом подстановки (замены переменой)
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (т.е. подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся.
Пусть требуется
найти интеграл
 .
Сделаем подстановку
.
Сделаем подстановку
 ,
где
,
где
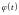 - функция, имеющая непрерывную производную.
- функция, имеющая непрерывную производную.
Тогда
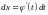 и на основании свойства инвариантности
формулы интегрирования неопределенного
интеграла получаем формулу интегрирования
подстановкой
и на основании свойства инвариантности
формулы интегрирования неопределенного
интеграла получаем формулу интегрирования
подстановкой
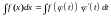 .
.
Формула также называется формулой замены переменных в неопределенном интеграле. После нахождения интеграла в правой части равенства следует перейти от новой переменной интегрирования t назад к переменной х.
Иногда целесообразно
подбирать подстановку в виде
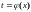 ,
тогда
,
тогда
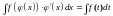 ,
где
.
Т. е. формулу можно применять справа
налево.
,
где
.
Т. е. формулу можно применять справа
налево.
Функцию
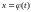 следует выбирать так, чтобы можно было
вычислить неопределенный интеграл,
стоящий в правой части равенства (2).
следует выбирать так, чтобы можно было
вычислить неопределенный интеграл,
стоящий в правой части равенства (2).
Приведем несколько примеров на интегрирование с помощью замены переменных.
Пример 1.
Найти
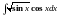 .
.
Сделаем подстановку
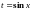 ,
тогда
,
тогда
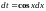 и, следовательно,
и, следовательно,
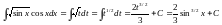
Пример 2.
Найти
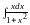 .
Полагаем
.
Полагаем
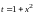 ,
тогда
,
тогда
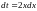 и
и
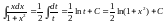
Пример 3.
Найти
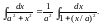 Полагаем
Полагаем
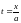 ;
тогда
;
тогда
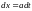 ,
,
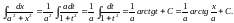
Пример 4.
Найти
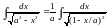 .
Полагаем
;
тогда
,
.
Полагаем
;
тогда
,
 (предполагается,
что a>0).
(предполагается,
что a>0).
Пример 5.
Найти
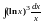 .
Полагаем
.
Полагаем
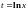 ,
тогда
,
тогда
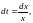
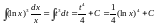 .
.
Пример 6.
Найти
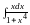 .
Полагаем
.
Полагаем
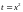 ,
тогда
,
,
тогда
,
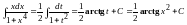
Метод замены переменных является одним из основных методов вычисления неопределенных интегралов. Успех интегрирования зависит в значительной степени от того, сумеем ли мы подобрать такую удачную замену переменных, которая упростила бы данный интеграл. Изучение методов интегрирования сводится к выяснению того, какую надо сделать замену переменной при том или ином виде подынтегрального выражения.
Метод интегрирования по частям
Пусть
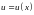 и
и
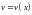 - функции имеющие непрерывные производные.
Тогда
- функции имеющие непрерывные производные.
Тогда
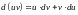 .
Интегрируя это равенство, получаем
.
Интегрируя это равенство, получаем
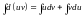 или
или
 .
.
Полученная формула
называется формулой
интегрирования по частям.
Она дает возможность свести вычисление
интеграла
 к вычислению интеграла
к вычислению интеграла
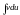 ,
который может оказаться существенно
более простым, чем исходный.
,
который может оказаться существенно
более простым, чем исходный.
Интегрирование по частям состоит в том, что подынтегральное выражение заданного интеграла представляется каким – либо образом в виде произведения двух сомножителей u и dv; затем, после нахождения v и du, используется формула интегрирования по частям.
Некоторые типы интегралов, которые удобно вычислять методом интегрирования по частям.
Интегралы вида
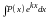 ,
,
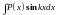 ,
,
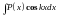 ,
где
,
где
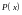 - многочлен, k
– число. Удобно положить
- многочлен, k
– число. Удобно положить
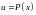 ,
а за dv
обозначить
остальные сомножители.
,
а за dv
обозначить
остальные сомножители.Интегралы вида
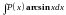 ,
,
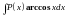 ,
,
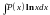 ,
,
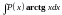 ,
,
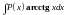 .
Удобно положить
.
Удобно положить
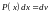 ,
а за u
обозначить остальные сомножители.
,
а за u
обозначить остальные сомножители.Интегралы вида
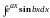 ,
,
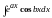 ,
где a
и b
– числа. За
,
где a
и b
– числа. За
 можно принять функцию
можно принять функцию
 .
.
Пример 1.
Найти
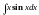 .
.
Положим
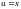 ,
,
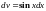 ,
тогда
,
тогда
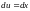 ,
,
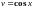 .Следовательно,
.Следовательно,
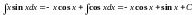 .
.
Замечание. При определении функции v по дифференциалу dv можно брать любую произвольную постоянную, так как в конечный результат она не входит. Поэтому удобно считать эту постоянную равной нулю.
Правило интегрирования
по частям применяется во многих случаях.
Так, например, интегралы вида
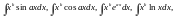 некоторые
интегралы, содержащие обратные
тригонометрические функции, вычисляются
с помощью интегрирования по частям.
некоторые
интегралы, содержащие обратные
тригонометрические функции, вычисляются
с помощью интегрирования по частям.
Пример 2.
Требуется вычислить
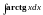 .
Положим
.
Положим
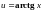 ,
,
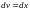 ,
тогда
,
тогда
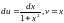 .
Следовательно,
.
Следовательно,
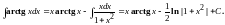
Пример 3.
Требуется вычислить
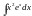 .
.
Положим
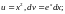 тогда
тогда
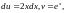
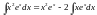 .
.
Последний интеграл снова интегрируем по частям, полагая
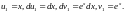 Тогда
Тогда
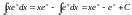 .
Окончательно будем иметь
.
Окончательно будем иметь
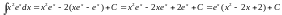 .
.
