
- •Неопределенный интеграл Понятие неопределенного интеграла
- •Свойства неопределенного интеграла
- •Основные методы интегрирования
- •Метод непосредственного интегрирования
- •Метод интегрирования способом подстановки (замены переменой)
- •Метод интегрирования по частям
- •Интегрирование тригонометрических функций.
- •Универсальная тригонометрическая подстановка
- •Интегралы типа , .
- •Использование тригонометрических преобразований
- •Интегрирование иррациональных функций.
- •Квадратичные иррациональности
- •Дробно – линейная подстановка
- •Интегрирование дифференциального бинома
- •Тригонометрическая подстановка
Интегрирование тригонометрических функций.
Рассмотрим
некоторые случаи нахождения интеграла
от тригонометрических функций. Функцию
с переменными
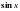 ,
,
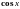 ,
над которыми выполняются рациональные
действия принято обозначать
,
над которыми выполняются рациональные
действия принято обозначать
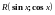 ,
где R
- знак рациональной функции.
,
где R
- знак рациональной функции.
Универсальная тригонометрическая подстановка
Вычисление
неопределенных интегралов типа
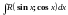 сводится к вычислению интегралов от
рациональной функции подстановкой
сводится к вычислению интегралов от
рациональной функции подстановкой
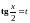 ,
которая называется универсальной.
,
которая называется универсальной.
Действительно,
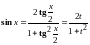 ,
,
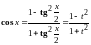 ,
,
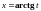 ,
,
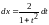 .
Поэтому
.
Поэтому
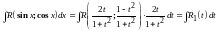 ,
,
где
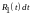 -
рациональная функция от t.
-
рациональная функция от t.
Удобны следующие правила:
Если функция нечетна относительно , т. е.
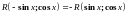 ,
то делается подстановка
,
то делается подстановка
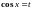 ;
;Если функция нечетна относительно , т. е.
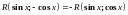 ,
то делается подстановка
,
то делается подстановка
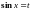 ;
;Если функция четна относительно и , т. е.
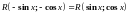 ,
то делается подстановка
,
то делается подстановка
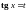 .
Такая же подстановка применяется, если
интеграл имеет вид
.
Такая же подстановка применяется, если
интеграл имеет вид
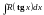 .
.
Пример
1. Вычислить
интеграл
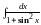 .
.
Решение:
Т.к. подынтегральная функция не
меняется при перемене знака у
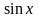 ,
то применим подстановку
,
то применим подстановку
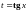 ,
тогда
,
тогда
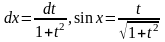 .
.
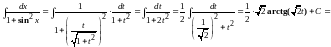
 .
.
Пример
2. Вычислить
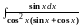 .
.
Решение:
Здесь можно
использовать универсальную подстановку,
но поскольку
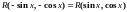 ,
положим
.
Тогда
,
положим
.
Тогда
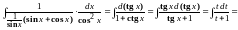
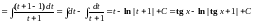 .
.
Интегралы типа , .
Для нахождения таких интегралов используются следующие приемы:
Подстановка , если
 – целое положительное нечетное число,
т.е.
– целое положительное нечетное число,
т.е.
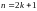 .
.
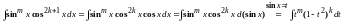
Мы получили интеграл от рациональной функции.
Подстановка
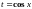 ,
если
,
если
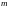 – целое положительное нечетное число,
т.е.
– целое положительное нечетное число,
т.е.
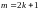 .
.Если
 и
и
 - целые неотрицательные четные числа
(
- целые неотрицательные четные числа
(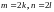 ),
то подынтегральное выражение преобразуют
с помощью следующих формул понижения
степени:
),
то подынтегральное выражение преобразуют
с помощью следующих формул понижения
степени:
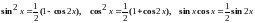 .
.Подстановка , если
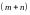 - четное отрицательное целое число.
- четное отрицательное целое число.
Пример
3. Вычислить
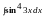 .
.
Решение:
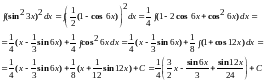 .
.
Пример
4. Вычислить
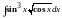 .
.
Решение:
Подынтегральная
функция меняет знак при перемене знака
у
,
то применим подстановку
.
Тогда
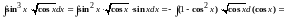
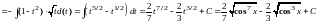 .
.
Пример
5. Вычислить
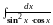 .
.
Решение:
Подынтегральная
функция меняет знак при перемене знака
у
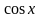 ,
то применим подстановку
.
Тогда
,
то применим подстановку
.
Тогда
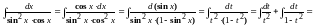
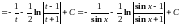 .
.
Пример
6. Вычислить
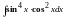 .
.
Решение: Подынтегральная функция представляет собой произведение четных степеней синуса и косинуса, поэтому применим формулы понижения степени:
 .
.
Пример
7. Вычислить
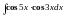 .
.
Решение: Воспользуемся формулой преобразования произведения тригонометрических функций в сумму:
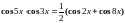
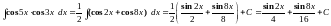
Пример
8. Вычислить
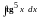 .
.
Решение: Понизим степень тангенса:
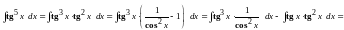
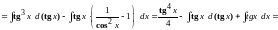
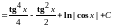 .
.
Использование тригонометрических преобразований
Интегралы
типа
 ,
,
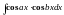 ,
,
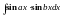 вычисляются с помощью известных формул
тригонометрии:
вычисляются с помощью известных формул
тригонометрии:
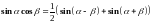
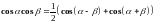
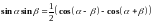
Интегрирование иррациональных функций.
Квадратичные иррациональности
Рассмотрим некоторые типы интегралов, содержащих иррациональные функции.
Интегралы типа
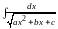 ,
,
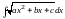 ,
,
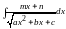 называют неопределенными интегралами
от квадратичных иррациональностей. Их
можно найти следующим образом: под
радикалом выделить полный квадрат
называют неопределенными интегралами
от квадратичных иррациональностей. Их
можно найти следующим образом: под
радикалом выделить полный квадрат
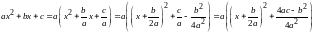 и сделать подстановку
и сделать подстановку
 .
При этом два первые интеграла приводятся
к табличным, а третий – к сумме двух
табличных интегралов.
.
При этом два первые интеграла приводятся
к табличным, а третий – к сумме двух
табличных интегралов.
Пример
1.
Найти интеграл
 .
.
Решение:
Так как
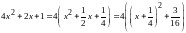 ,
то
,
то
 .
Сделаем подстановку
.
Сделаем подстановку
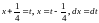 .
Тогда
.
Тогда
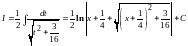 .
.
Пример
2.
Найти интеграл
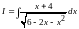 .
.
Решение:
Тек как
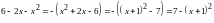 ,
то подстановка имеет вид
,
то подстановка имеет вид
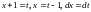 .
.
Тогда,
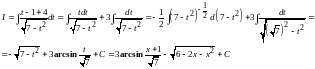 .
.
Интегралы
типа
 ,
где
,
где
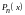 - многочлен степени n,
можно вычислять, пользуясь формулой
- многочлен степени n,
можно вычислять, пользуясь формулой
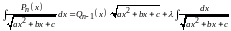 ,
где
,
где
 - многочлен степени
- многочлен степени
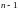 с неопределенными коэффициентами,
- также неопределенный коэффициент.
с неопределенными коэффициентами,
- также неопределенный коэффициент.
Все неопределенные коэффициенты находятся из тождества, получаемого дифференцированием обеих частей равенства
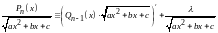 ,
после чего необходимо приравнять
коэффициенты при одинаковых степенях
неизвестной x.
,
после чего необходимо приравнять
коэффициенты при одинаковых степенях
неизвестной x.
