
Вопрос 1
Объединением
множеств
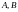 называется
называется
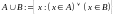 .
Пересечением множеств
называется
.
Пересечением множеств
называется
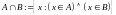 .
Разностью множеств
называется
.
Разностью множеств
называется
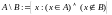 .
.
Вопрос 2
Рациональное
число —
число, представляемое несократимой обыкновенной
дробью ![]() ,
где числитель m —целое
число,
а знаменатель n — натуральное
число.
Периодическая
дробь бесконечная
десятичная дробь, в которой, начиная с
некоторого места, стоит только периодически
повторяющаяся определённая группа
цифр. Например, 1,3181818...;
,
где числитель m —целое
число,
а знаменатель n — натуральное
число.
Периодическая
дробь бесконечная
десятичная дробь, в которой, начиная с
некоторого места, стоит только периодически
повторяющаяся определённая группа
цифр. Например, 1,3181818...;
Вопрос 3
Множество
точек
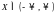 называется ограниченым сверху
называется ограниченым сверху
(снизу)
если
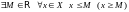 ;
множество ограничено, если оно
;
множество ограничено, если оно
ограниченно
и сверху и снизу:
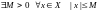 .
Точной верхней (нижней) гранью множества
.
Точной верхней (нижней) гранью множества
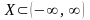 называется наименьшее (наибольшее)
число
называется наименьшее (наибольшее)
число

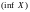 со свойствами
со свойствами

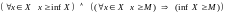 .
.
Вопрос 4
Множества
называются равномощными, если существует
биекция
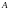 на
на
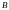 .
Мощностью конечного множества называется
число его элементов.
.
Мощностью конечного множества называется
число его элементов.
Обозначение
 .
Определение Множество называется
счетным, если оно равномощно множеству
.
Определение Множество называется
счетным, если оно равномощно множеству
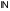 .
Множество называется множеством мощности
континуум, если оно равномощно множеству
.
Множество называется множеством мощности
континуум, если оно равномощно множеству
 .
Множество элементов называется
упорядоченным, если для любых его двух
элементов всегда можно сказать, что
один из них предшествует другому.
.
Множество элементов называется
упорядоченным, если для любых его двух
элементов всегда можно сказать, что
один из них предшествует другому.
Вопрос 5
Отображение
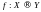 называется
инъективным (взаимно однознач ным), если
она разным элементам из
называется
инъективным (взаимно однознач ным), если
она разным элементам из
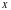 сопоставляет разные элементы из
сопоставляет разные элементы из
 .
Отображение
называется сюръективным (отображением
"на"), если
.
Отображение
называется сюръективным (отображением
"на"), если
 .
Отображение
.
Отображение
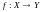 называется биективным (биекцией), если
она инъективно и сюръективно. Биективное
отображение и только такое отображение
имеет обратное
называется биективным (биекцией), если
она инъективно и сюръективно. Биективное
отображение и только такое отображение
имеет обратное
 .
При этом область определения последнего
есть
.
.
При этом область определения последнего
есть
.
Вопрос 6
Композицией
отображений
и
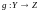 называется
отображение
называется
отображение
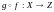 ,
определяемое по правилу
,
определяемое по правилу
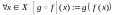 .
Преобразование
.
Преобразование
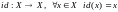 ,
называется тождественным отображением.
,
называется тождественным отображением.
Пусть
и
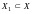 .
Сужением отображения
.
Сужением отображения
 на подмноже ство
на подмноже ство
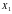 называется отображение
называется отображение
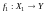 определяемое по правилу
определяемое по правилу
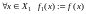 .
Обозначение.
.
Обозначение.
 .
.
Вопрос 7
Отображение
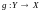 называется правым (левым) обратным к
отображению
,
если
называется правым (левым) обратным к
отображению
,
если
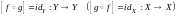 .
.
Отображение
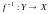 называется обратным к отображению
,
если оно является и правым и левым
обратным к
.
называется обратным к отображению
,
если оно является и правым и левым
обратным к
.
ЗАМЕЧАНИЕ 1) Отображение является инъективным тогда и только тогда, когда оно имеет левое обратное отображение.
2) Отображение является сюръективным тогда и только тогда, когда оно имеет правое обратное отображение.
3) Отображение является биекцией тогда и только тогда, когда оно имеет обратное отображение.
Вопрос 8
Функция называется элементарной, если она получена из основных элементарных с помощью конечного числа, операций сложения, вычитания, умножения, деления, возведения в степень и композиции.
Следующие 5 классов функций называются основными элементарными:
1)
Степенные
 .
.
2)
Показательные
 .
.
3)
Логарифмические 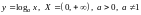 .
.
4)
Тригонометрические
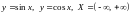 .
.
5)
Обратные тригонометрические
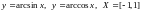 .
.
Вопрос 9
Гиперболи́ческие фу́нкции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями. Рациональная функция — это дробь, числителем и знаменателем которой являются многочлены. Она имеет вид
![]()
где
![]() ,
,
![]() — многочлены от
любого числа переменных.
— многочлены от
любого числа переменных.
Частным случаем являются рациональные функции одного переменного:
![]() ,
где P(x) и Q(x) — многочлены.
,
где P(x) и Q(x) — многочлены.
Фу́нкция
Дирихле́ — функция ![]() ,
принимающая значение 1, если аргумент
есть рациональное
число,
и значение 0, если аргумент есть иррациональное
число,
,
принимающая значение 1, если аргумент
есть рациональное
число,
и значение 0, если аргумент есть иррациональное
число,
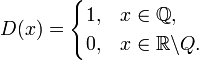
Так как функция разрывна в каждой точке (между любыми двумя рациональными числами есть хотя бы одно иррациональное), то её график нарисовать невозможно, но мысленно можно представить.
Так как в любой окрестности любой точки вещественной прямой содержатся как рациональные, так и иррациональные числа (а значит, как нули, так и единицы функции), ни в одной точке у D(x) нет предела, а значит, она разрывна на всей числовой прямой, причём все точки разрыва — второго рода.
