1. Для какого канала и на что дает ограничение теорема Шеннона?

«Если канал связи с финитной АЧХ и аддитивным белым гауссовским шумом (АБГШ) обладает пропускной способностью «С», а производительность источника равна Н′(А), то при Н^′(А) ≤ С возможно такое кодирование, которое обеспечивает передачу сообщений по этому каналу со сколь угодно малыми ошибками и со скоростью, сколь угодно близкой к значению «С» »:

[бит/с], (3.1)

где ∆f_k– ширина полосы прямоугольной АЧХ канала связи;

Р_с- средняя мощность сигнала;

Р_ш=N₀·∆f_k; (3.2)

N₀·- односторонняя спектральная плотность АБГШ.

Для дискретного канала и случайного кодирования источника эта теорема может быть записана в другой форме

(3.3)

где 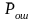- средняя по множеству кодов вероятность ошибки декодирования;

Т- длительность кодового блока укрупненного источника сообщений.

Т.к., [С−Н^′(А) ≥ 0] по условию теоремы, то с увеличением Т (укрупнением источника) 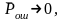причем при Н^′(А)→С значение Т→∞ и увеличивается задержка декодирования кода укрупненного источника.

2. На что влияет длина кодируемого отрезка сообщения?

чем длиннее кодируемый отрезок сообщения (Т) и чем менее эффективно

используется пропускная способность канала ( чем больше разность [С-Н^′(А)]), тем выше достоверность связи (1- );

существует возможность обмена между эффективностью использования, значениями С, и Т (задержкой декодирования).

3. Чему равна пропускная способность канала связи при бесконечной его полосе?

При ∆f_k→∞ . Тогда разложим функцию ln(1+x) в ряд Маклорена (т.е. в точке х=0) , который при х→0 равен ln(1+x)≈x. В результате получим

.

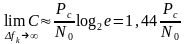Пропускная способность заметно возрастает с увеличением ∆f_k до тех пор, пока Р_с/Р_ш≥1 и стремится к пределу 1,44 Р_с/N₀, т.е. максимальное значение параметра С имеет место при h →0.

4. Что определяет зависимость удельных энергетических затрат βЕ от затрат полосы β∆f и чему равны βЕ для передачи по каналу одного бита информации при β∆f → ?

В результате выражение

(3.5)

определяет связь между удельными затратами энергии и полосы в канале с АБГШ и финитной АЧХ. Вместе с тем, т.к.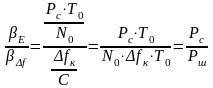

то из (3.5) получим зависимость для отношения сигнал/шум (ОСШ):

. (3.6)

Это выражение определяет необходимое значение ОСШ в оптимальном канале связи с АБГШ в зависимости от удельных затрат полосы частот канала связи.

При больших значениях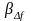

,

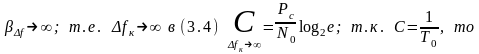
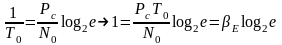т.е. для передачи одного бита (С =1) необходимы малые и ОСШ.

5. Как зависят удельные затраты полосы и энергии от алфавита источника при полосе сигнала в канале, согласованном с источником, и в канале с ограниченной полосой?

Найдем зависимость β_Е от значения алфавита М. Мы получили равенство (3.5)

,

уменьшаемое в скобках которого , с учётом предыдущего равенства (3.7)

для при Б_с» 1, равно . / /

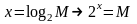После подстановки этого значения в (3.5) получим:

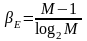. (3.8)

При М=2 получим 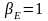, =1. С увеличением М растет β_Еи уменьшается согласно (3.7), например, при М=4 → , =0,5.

Следует отметить, что уменьшение в (3.7) за счет увеличения M источника (т.е. М >М_кс) при ∆f_k-const ведет к уменьшению длительности Т₀=Т_кс сигнала в канале. Это может привести к межсимвольной интерференции сигналов на выходе канала связи с ограниченной полосой. Поэтому, чтобы компенсировать уменьшение длительности Т₀или увеличить её, применяются М-уровневые канальные сигналы или укрупнение алфавита источника сообщения в блоки для кодирования и передачи по каналу комбинаций М-уровневых сигналов блока с управляемой межсимвольной интерференцией. При этом реализуют прием «в целом» блока в демодуляторе.

6. Виды многоуровневых спектрально эффективных сигналов и соответствующее им расположение векторов.

.

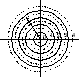
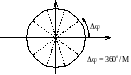
многоуровневый АМ сигнал Многоуровневый ФМ сигнал Комбинированные АМ и ФМ сигналы

7. Чему равно минимальное значение базы сигнала для энергетически эффективной двоичной системы связи?

В оптимальной системе источник сообщения согласован с каналом(Н^′(А)=С) и удельные затраты полосы канала (на 1 бит информации) равны:

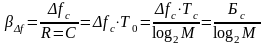(3.7)

где 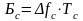база сигнала с полосой 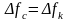. Минимально допустимое значение базы ≈1. Сигналы с базой £ 2 называются простыми сигналами. Сигналы с базой > 2 называются сложными.

8. Можно ли говорить, что оптимизация системы связи заключается в выборе вида сигналов? Чему равно расстояние между сигналами при равных энергиях?

При оптимизации системы ищется наилучший вид сигнала для заданного радиоканала и соответствующий оптимальный способ приема

9. Привести примеры типовых спектрально эффективных сигналов и соответствующие значения расстояния между сигналами.

Бинарные противоположные сигналы.

В этом случае М=2, т.е. требуется образование сигналов S(t, x₁) и S(t, x₂), достаточно N=1. Векторы

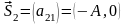
направлены противоположно друг другу

,

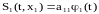R= -1

Рис.3.7. Вершины векторов бинарных противоположных сигналов.

Бинарные ортогональные сигналы.

В этом случае при М=2 достаточно N=2.

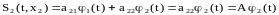
Рис.3.8. Вершины векторов бинарных ортогональных сигналов.

Бинарные ортогональные сигналы обеспечивают меньшее расстояние между концами векторов, чем противоположные сигналы. Однако на практике иногда такого рода сигналы используются.

М-арные ортогональные сигналы.

В этом случае N=M, и число ортогональных функций численно равно размеру алфавита. Каждому x_i соответствует свояj_j, т.е.

……………….

.

При этом, j_j(t) могут быть ортогональные гармонические функции и

x₁ передаётся сигналом .

x₂ передаётся сигналом .

……………………………………

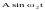x_N передаётся сигналом .

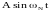Для удовлетворения условия ортогональности частоты w₁, w₂, ... , w_N должны быть кратны частоте . Только в этом случае

,

где n и m - целые числа и R=0.

Биортогональные сигналы.

Пусть М - размер алфавита - чётное число. Образуем ортогональных сигналов 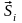. Кроме того, для каждого сигнала образуем противоположный ему сигнал .

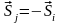Для N = 2:

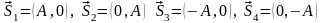
Рис.3.9. Вершины векторов биортогональных сигналов.

Сигналы с прямоугольной конфигурацией векторов.

Для образования такого рода сигналов берётся N колебаний j_j(t). Размер алфавита М при этом может быть равен 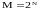. При этом геометрическая конфигурация векторов выбирается такой, чтобы концы векторов находились в вершинах N-мерного куба.

Например, при N=2

Двумерный куб (квадрат)

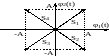
Рис.3.10. Вершины векторов сигналов с прямоугольной конфигурацией векторов.

Пример реализации функции j_j(t)и соответствующих сигналов при N=2, М =4 представлен на рис.3.11.

Рис.3.11. Пример реализации функции j_j(t) исигналов с прямоугольной конфигурацией векторов.