1.13.Оценка среднего квадратического отклонения результатов наблюдений

Несмещенной состоятельной, эффективной оценкой для генерального среднего ā нормального распределения является выборочное среднее х,

определяемое по формуле:

Где х₁; х₂;…;х_n – совокупность значений случайных величин х.

Несмещенную оценку для среднего квадратического отклонения определяют по формуле:

где

если a неизвестно, то по формуле (1):

(1)

если а известно, то по формуле (2):

(2)

Значение коэффициента Мк дается в таблице, где к = n-1, если а неизвестно, и к = n, если а известно.

При значениях объема выборок n > 60 оценку для среднего квадратического отклонения σ находят по формуле (1), а если а неизвестно, или по формуле (2), если а известно.

Несмещенными оценками для дисперсии σ² нормального распределения являются выборочные характеристики:

при неизвестном а

при известном а

1.14.Оценка среднего квадратического отклонения результата измерения

Среднее квадратическое отклонение результата измерения оценивают по формуле:

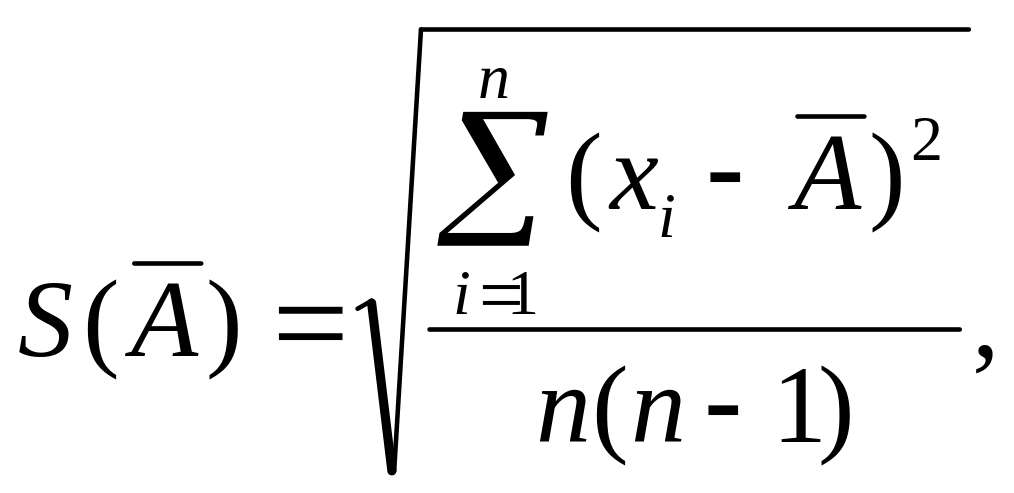
где S(Ã) – оценка среднего квадратического отклонения результата измерения;

à – результат измерения (ср. арифметическое исправленных результатов наблюдений); х_i – i-й результат наблюдений.

1.15. Вычисление доверительных границ случайной погрешности результата измерения

Доверительные границы случайной погрешности результата измерения устанавливают для результатов наблюдений, принадлежащих нормальному распределению. Если это условие не выполняется, то методы вычисления доверительного интервала случайной погрешности должны быть указаны в методике выполнения конкретных измерений.

Если заранее известно, что результаты наблюдений принадлежат нормальному распределению, доверительные границы Є (без учета знака) случайной погрешности результата измерения находят по формуле:

Є=t_sS( )

Где t_s – коэффициент Стьюдента, который в зависимости от доверительной вероятности Р и числа результатов наблюдений n находят по таблицам. При числе наблюдений n > 50 для проверки принадлежности их к нормальному распределению используют критерий х² (Пирсона) или ω² (Мизеса-Смирнова). Если 50 > n > 15, то используют составной критерий.

1.16. Вычисление доверительных границ погрешности результата измерени3

1

Если отношение неисключенных систематических погрешностей к среднему квадратическому отклонению результата измерения Q/S(Ã) < 0,8, то неисключенными систематическими погрешностями пренебрегают и принимают что граница погрешности результата ∆ = Є. Если Q/S(Ã) > 8, то пренебрегают случайной погрешностью и принимают, что граница погрешности результата Δ = Q. Однако , следует помнить, что погрешность, возникающая вследствие пренебрежения одной из составляющих погрешности результата измерений при выполнении указанных неравенств, не должна превышать 15 %. Если неравенства не выполняются, то границу погрешности результата измерения находят путем построения композиции распределений случайных и не исключенных систематических погрешностей, рассматриваемых как случайные величины.

В результате определения доверительных границ случайных погрешностей, вычисляют границы погрешности результата измерения Δ без учета знака по формуле:

Δ = К*S_Σ

Где К – коэффициент, зависящий от соотношения случайной и неслучайной систематической погрешностей;

S_Σ – оценка суммарного среднего квадратического отклонения результата измерения.

К оэффициент К вычисляют по эмпирической формуле:

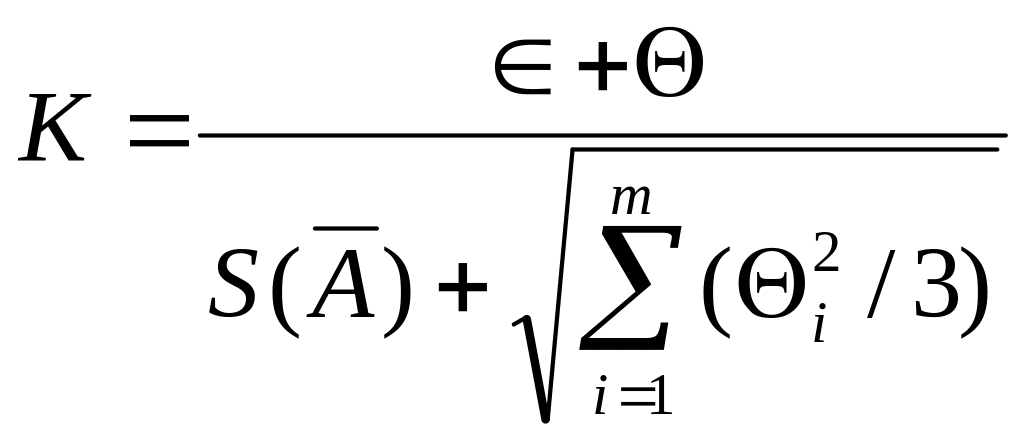
Суммарное среднее квадратического отклонение результата измерения оценивают по формуле: Є