32. Постановка задачи проверки статистических гипотез.

Пусть в (статистическом) эксперименте доступна наблюдению случайная величина X, распределение которой неизвестно полностью или частично. Тогда любое утверждение, касающееся называется статистической гипотезой. Гипотезы различают по виду предположений, содержащихся в них:

• Статистическая гипотеза, однозначно определяющая распределение , то есть 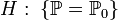, где 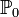какой-то конкретный закон, называется простой.

• Статистическая гипотеза, утверждающая принадлежность распределения к некоторому семейству распределений, то есть вида 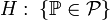, где 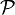 — семейство распределений, называется сложной.

На практике обычно требуется проверить какую-то конкретную и как правило простую гипотезу H₀. Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза H₁, называемая конкурирующей или альтернативной.

Выдвинутая гипотеза нуждается в проверке, которая осуществляется статистическими методами, поэтому гипотезу называют статистической. Для проверки гипотезы используют критерии, позволяющие принять или опровергнуть гипотезу.

В большинстве случаев статистические критерии основаны на случайной выборке фиксированного объема из распределения . В последовательном анализе выборка формируется в ходе самого эксперимента и потому её объем является случайной величиной (см. Последовательный статистический критерий).

33. Лемма Неймана – Пирсона.

-лемма, утверждающая, что в задаче статнетич. проверки простой гипотезы Н _о против простой альтернативы Н ₁ отношения правдоподобия критерий является наиболее мощным критерием среди всех статистич. критериев, имеющих один и тот же заданный значимости уровень.

34. Однородное интегральное уравнение Фредгольма.

35. Отношение правдоподобия нормальных выборок.

36. Статистика проверки гипотез.

Статистическая проверка гипотез, система приёмов в математической статистике, предназначенных для проверки соответствия опытных данных некоторой статистической гипотезе. Процедуры С. п. г. позволяют принимать или отвергать статистические гипотезы, возникающие при обработке или интерпретации результатов измерений во многих практически важных разделах науки и производства, связанных с экспериментом. Правило, по которому принимается или отклоняется данная гипотеза, называется статистическим критерием. Построение критерия определяется выбором подходящей функции Т от результатов наблюдений, которая служит мерой расхождения между опытными и гипотетическими значениями. Эта функция, являющаяся случайной величиной, называется статистикой критерия, при этом предполагается, что распределение вероятностей Т может быть вычислено при допущении, что проверяемая гипотеза верна. По распределению статистики Т находится значение Т₀, такое, что если гипотеза верна, то вероятность неравенства T >T₀ равна a, где a — заранее заданный значимости уровень.

38. Неоднородное интегральное уравнение Фредгольма.

В математике интегральное уравнение Фредгольма — это интегральное уравнение, ядром которого является ядро Фредгольма. Названо так по имени изучавшего его Ивара Фредгольма. Со временем выросло в самостоятельный раздел функционального анализа — теорию Фредгольма, которая изучает ядра Фредгольма и операторы Фредгольма.

Общая теория, основанная на уравнениях Фредгольма, известна как теория Фредгольма. В теории рассматривается интегральное преобразование специального вида

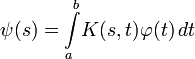
где функция K называется ядром уравнения, а оператор A, определяемый как

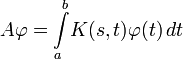, называется оператором (или интегралом) Фредгольма.

Одним из основополагающих результатов является факт, что ядро K есть компактный оператор, известный иначе как оператор Фредгольма. Компактность может быть показана с помощью равномерной непрерывности. Как к оператору, к ядру может быть приложена спектральная теория, изучающая спектр собственных значений.

39. Рабочая характеристика.

40. Корреляционный приём

Оптимальное когерентное (двоичное) пороговое обнаружение слабого сигнала в аддитивном шуме определяется главным образом квадратным корнем из отношения сигнал/шум на входе по мощности, а само устройство для обнаружения должно определять усредненную обобщенную взаимную корреляцию принятых данных с сигналом.

41. Согласованная фильтрация.

линейный оптимальный фильтр, построенный исходя из известных спектральных характеристик полезного сигнала и шума

42. “Сверхобнаружение”

43. Свойства точечных оценок.

• Оценка 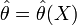называется несмещённой, если её математическое ожидание равно оцениваемому параметру генеральной совокупности:

,

где обозначает математическое ожидание в предположении, что θ — истинное значение параметра (распределения выборки X).

• Оценка 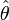называется эффективной, если она обладает минимальной дисперсией среди всех возможных несмещенных точечных оценок.

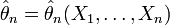• Оценка называется состоятельной, если она по вероятности с увеличением объема выборки n стремится к параметру генеральной совокупности: ,

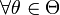по вероятности при .

• Оценка 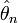называется сильно состоятельной, если ,

почти наверное при .

Это заготовка статьи по математике. Вы можете помочь проекту, исправив и дополнив её.

44. Эффективность точечных оценок.

Точечное оценивание - это вид статистического оценивания, при котором значение неизвестного параметра приближается отдельным числом. То есть необходимо указать функцию от выборки (статистику)

,

значение которой будет рассматриваться в качестве приближения к неизвестному истинному значению .

К общим методам построения точечных оценок параметров относятся: метод максимального правдоподобия, метод моментов, метод квантилей.

Ниже приводятся некоторые свойства, которыми могут обладать или не обладать точечные оценки.

45. Неравенство Рао – Крамера.

В математической статистике неравенством Краме́ра — Ра́о (в честь Гаральда Крамера и К. Р. Рао) называется неравенство, которое при некоторых условиях на статистическую модель даёт нижнюю границу для дисперсии оценки неизвестного параметра, выражая её через информацию Фишера.

Пусть дана статистическая модель , — выборка размера n, определена функция правдоподобия и выполнены следующие условия (условия регулярности):

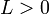• и везде дифференцируема по .

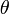• Функция 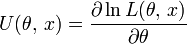(функция вклада выборки) имеет конечную дисперсию (или, что то же, конечна информация Фишера).

• Для любой статистики 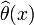с конечным вторым моментом имеет место равенство

.

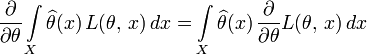Пусть при этих условиях дана статистика , которая несмещённо оценивает дифференцируемую функцию τ(θ). Тогда справедливо следующее неравенство:

• ;

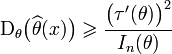• равенство достигается тогда и только тогда, когда 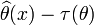представляется в виде .

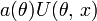Здесь — информация Фишера.