Вопросы к тестированию по курсу “Моделирование систем”

1 Линейные системы.

Системы управления называют линейными, если выполняются принцип суперпозиции. Если этот принцип несправедлив, то систему называют нелинейной.

            Сущность принципа суперпозиции заключается в том, что линейной комбинации произвольных входных сигналов  соответствует линейная комбинация соответствующих выходных сигналов: .

            Принцип суперпозиции всегда выполняется, если выполняются следующие два условия:

1)  при суммировании любых двух входных сигналов соответствующие выходные сигналы суммируются;

2)  при любом увеличении (уменьшении) входного сигнала без изменения его формы выходной сигнал увеличивается (уменьшается) во столько же раз, также не изменяя своей формы.

2. Весовая функция.

Введем функцию , которая представляет собой выходной сигнал системы управления при входном сигнале в виде -функции. Функция  называется импульсной переходной характеристикой системы или весовой функцией.

3. Свёртка.

    Эта формула называется интегралом Дюамеля или интегралом свертки. Ее смысл заключается в том, что выходной сигнал любой линейной системы получается с помощью взвешивания и последующего интегрирования входного сигнала  с весовой функцией .

4. Тест – сигналы.

5. Переходная функция.

Переходная функция h(t) — в теории управления реакция динамической системы на входное воздействие в виде функции Хевисайда,при нулевых начальных условиях. Зная переходную характеристику, можно определить реакцию системы y(t) на произвольное входное воздействие x(t) с помощью интеграла Дюамеля-Карсона:

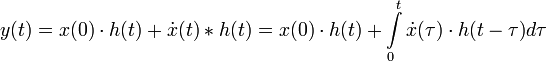, где

 — свёртка двух функций.

6. Дискретная свёртка.

Для дискретных по времени систем связь выхода и входа определяется дискретной сверткой входа и импульсной характеристики , то есть:

и

где импульсная характеристика системы - это ее реакция на единичный импульс

7. Разностное уравнение.

РАЗНОСТНЫЕ УРАВНЕНИЯ [difference equations] — уравнения, содержащие конечные разности искомой функции. (Конечная разность определяется как соотношение, связывающее дискретный набор значений функции y = f(x), соответствующих дискретной последовательности аргументов x₁, x₂, ..., x_n.)

8. Случайные события и величины.

9. Вероятность.

10. Условная вероятность.

11. Плотность и функция распределения.

12. Нормальное распределение.

13. Формула Байеса.

Если стало известно, что в результате испытания событие  произошло, то условная вероятность гипотезы  (апостериорная вероятность гипотезы ) определяется по формуле Бaйeca:

                                        

14. Моменты случайных величин.

15. Дисперсия, корреляционный момент.

16. Случайные процессы и последовательности.

Случа́йный проце́сс (случайная функция) в теории вероятностей — семейство случайных величин, индексированных некоторым параметром, чаще всего играющим роль времени или координаты. Другое определение: Случайным называется процесс u(t), мгновенные значения которого являются случайными величинами.

Пусть дано вероятностное пространство . Параметризованное семейство случайных величин

,

где T произвольное множество, называется случайной функцией.

17. Стационарные процессы

Случайный процесс называется стационарным, если все многомерные законы распределения зависят только от взаимного расположения моментов времени , но не от самих значений этих величин. Другими словами, случайный процесс называется стационарным, если его вероятностные закономерности неизменны во времени. В противном случае, он называется нестационарным.

18. Функция корреляции.

Ряд задач решается с использованием двумерной функции распределения. Знание двумерной плотности распределения веро­ятности позволяет вычислить смешанный второй начальный мо­мент двумерного закона распределения или функцию корреля­ции:

19. Корреляционная матрица.

матрица коэффициентов корреляции нескольких случайных величин. Если X₁, ..., Х _п - случайные величины с ненулевыми дисперсиями то элементы р, у при равны корреляции коэффициентам р( Х _i, X_j), а при i=j равны 1. Свойства К. м. Р определяются свойствами ковариационной матрицы, е в силу соотношения: е= ВРВ, где В - диагональная матрица с диагональными элементами s₁, ..., s_n. А. В. Прохоров.

20. Многомерное нормальное распределение.

Многоме́рное норма́льное распределе́ние (или многоме́рное га́уссовское распределе́ние) в теории вероятностей — это обобщение одномерного нормального распределения.

Случайный вектор имеет многомерное нормальное распределение, если выполняется одно из следующих эквивалентных условий:

• Произвольная линейная комбинация компонентов вектора 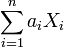имеет нормальное распределение или является константой.

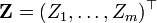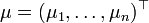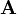• Существует вектор независимых стандартных нормальных случайных величин , вещественный вектор и матрица размерности 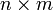, такие что:

.

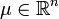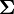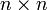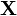• Существует вектор и неотрицательно определённая симметричная матрица размерности , такие что характеристическая функция вектора имеет вид:

.