3. Структурные преобразования механизмов

Представление механизма в виде структурных групп зависит от расположения входа (входного звена). Если перенести вход в механизме, то изменится его структура. Структурное преобразование состоит в условном перенесении входов, целью которого является упрощение структуры механизма.

Рассмотрим механизм, представленный на рис.1.24, а. Если в качестве входного звена выбрать звено DF, то весь механизм разобьется на три структурные группы: однозвенную одноподвижную (звено DF со вращательной КП), диаду ВВВ (звенья CD и CE с тремя вращательными КП) и еще одну диаду ВВВ (звенья ОА и АВ с тремя вращательными парами). Граф структуры преобразованного механизма представлен на рис. 1.24, б. В результате структурного преобразования мы условно избавились от громоздкой четырехзвенной группы, заменив ее на две диады.

При исследовании механизмов с несколькими степенями подвижности часто используется структурное преобразование, называемое, по предложению проф. М.З. Коловского, структурной инверсией. При структурной инверсии выходные координаты механизма (координаты рабочих органов) рассматриваются как входные, а обобщенные координаты входных звеньев и пар – как выходные.

Рассмотрим пример. На рис.1.25, а представлена схема плоской платформы. Число степеней подвижности по формуле Чебышева W_п=3(6–1) –26=3. Следовательно, в механизме надо задать три входа: q₁, q₂, q₃. В случае, если эти входы заданы так, как показано на рисунке, механизм распадается на следующие структурные группы: две однозвенные одноподвижные (звенья ОА и DE с вращательными КП) и одну трехзвенную одноподвижную (звенья АВ, ВС, CD с четырьмя вращательными КП). Граф структуры такого механизма показан на рис.1.25, б. Выходными координатами в этом случае являются координаты некоторой точки М звена ВС и угол наклона этого звена . Выполним структурную инверсию механизма. Примем координаты х_м, у_м,  за входные, а обобщенные координаты q₁, q₂, q₃ – за выходные. Тогда структура механизма изменится, а граф структуры будет таким, как показано на рис. 1.25, в: к стойке присоединена однозвенная трехподвижная группа (звено ВС: W=31–0=3), которая связана с двумя группами Ассура типа ВВВ (диады, включающие в себя звенья ОА и АВ с одной стороны, и CD и DE – с другой). Тем самым мы понизили максимальное число звеньев в структурных группах с трех до двух.

Билет №8. Геометрический анализ замкнутых механизмов. Пример.

Зависимость выходных параметров от входных обобщенных координат механизма называется функцией положения механизма.

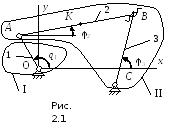
Для механизма, показанного на рис. 2.1:

(2.1)

Определение функций положения механизма составляет прямую задачу геометрического анализа.

Рассмотрим последовательность составления функции положения х_К(t)=П_ХК[q₁(t)], y_K(t)=П_YК[q₁(t)]

1.Проводится структурный анализ механизма:

• Однозвенная одноподвижная СГ I (кривошип 1 и вращательную пару О),

• Диада ВВВ, содержащую звенья 2 и 3 и три вращательные пары А, В и С.

2.В каждой структурной группе вводятся входные и выходные координаты.

3.Путем размыкания некоторых кинематических пар структурные группы приводят к открытым кинематическим цепям типа «дерево».

4.Вводятся групповые координаты, определяющие, вместе с входными, положение звеньев «дерева». Число групповых координат должно быть равно числу разомкнутых связей (на рис. 2.1 это углы ₂ и ₃).

5.Составляются условия замыкания ранее разомкнутых связей и функции положения. На основе этих условий получаются групповые уравнения, связывающие входные, выходные и групповые координаты структурной группы.

Функции положения для группы I:

(2.2)

Групповые уравнения для группы II:

(2.3)

Уравнения получены из условия замыкания связей в шарнире В (неизвестны групповые координаты ₂ и ₃)

Функции положения точки К группы II:

(2.3)

ФП для механизма с несколькими (W) степенями подвижности:

s = 1, …, m, (2.4)

где m – число выходных координат.

Составление функций положения на примере плоской платформы (рис. 2.2).

1. Структурный анализ механизма.

Три структурные группы:

• однозвенные одноподвижные I и II,

• трехзвенную одноподвижную III.

2. Введем входные и выходные координаты.

Группа I: вход х_О, у_О, q₁,

выход х_А, у_А;

Группа II: вход х_Е, у_Е, q₂,

выход x_D, y_D;

Группа III: вход х_А, у_А, х_D, y_D, q₃,

выход х_М, у_М, ₃.

3.Произведем размыкание группы III в шарнире C

4.Введем групповые координаты: ₂, ₃, и ₄.

5.Запишем условия замыкания: x_C3 = x_C4, у_C3 = y_C4.

Составим групповые уравнения:

Группа I,II:

,

Группа III:

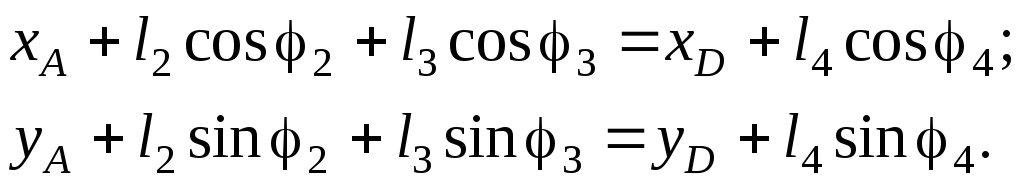(2.5)

Дополнительное уравнение для углов:

₃ + q₃ = ₄. (2.6)

Обратная задача геометрического анализа: определение обобщенных входных координат в зависимости от выходных, т.е. отыскание функций:

q_к = Ф_к (х₁, … , х_m), к = 1, … , W. (2.7)

• m= W (число выходных координат равно числу степеней подвижности):

задача может иметь одно или несколько решений;

• m> W:

задача в общем случае не имеет решения;

• m< W:

задача имеет бесконечное число решений (некоторое число координат (а именно W – m) можно задать произвольно).

Пример трехподвижной платформы. Дано: х_М, у_М, ₃.

Определить: q₁, q₂, q₃.

Структурный анализ инверсного механизма.

Три структурные группы:

• однозвенная трехподвижная I ,

• II и III – двухзвенные группы Ассура типа ВВВ..

Составим уравнения для группы I:

(2.8)

Для группы II :

(2.9)

Для группы III:

(2.10)

Дополнительное уравнение для углов: ₃ + q₃ = ₄.

Билет №9. Решение групповых уравнений

Если групповые уравнения имеют решение, то оно, как правило, является не единственным.

Определяем: из второго уравнения находим sin₂,

находим ,

подставляем в первое выражение и находим x_B.

, где – способ сборки.

Шарнирный четырехзвенник.

М = 1 (положение АВ₂С ) – обход шарниров в последовательности А,В,С происходит против часовой стрелки.

М = –1 (положение АВ₁С ) – обход шарниров в последовательности А,В,С происходит по часовой стрелке.

Особое или сингулярное положение (если АВ+ВС=ОА+ОС при определенном q сборки совпадают).

В механизме, в котором существует особое положение, после его прохождения возможна перемена способа сборки и, следовательно, реализация побочного решения групповых уравнений.

Следует избегать такого сочетания размеров, при котором возможно особое положение.

Трехподвижная платформа.

Две разные конфигурации груп­пы:

АВСD: АВ₁С₁D и АВ₂С₂D.

Билет №10. Решение уравнений геометрического анализа для одноподвижных и многоподвижных механизмов методом Ньютона.

Решение групповых уравнений на ЭВМ

Пусть одно решение групповых уравнений механизма уже получено.

Координаты, соответствующие этому положению, обозначим знаком (*): q₁=q_1*, q₂=q_2*, q₃=q_3*, ₂=_2*, ₃=_3*.

Дадим малые приращения входных координат q₁, q₂, q₃.

Получим новые значения входных координат: q₁=q_1*+q₁, q₂=q_2*+q₂, q₃=q_3*+q₃.

Тогда решение ₂ и ₃ будет единственным, поскольку второе положение механизма, соответствующее тем же приращениям координат q₁, q₂ и q₃, окажется далеким от исходного положения механизма.

Определим малые приращения ₂ и ₃ из групповых уравнений:

При этом предположим, что приращения х_А, у_А, х_D, у_D уже получены решением групповых уравнений групп I и II.

Или в обобщенной форме:, (2.11)

где – векторы-столбцы:

При этом;

. (2.12)

Мы ищем решение векторного уравнения

(2.13)

Метод Ньютона или метод касательных. В соответствии с этим методом (k+1)-е приближение для связывается с k-м приближенным соотношением k = 1, 2, Доказано, что в достаточно малой окрестности исходного решения последовательность (2.14) сходится, причем обеспечивается квадратичная сходимость. Выражение .

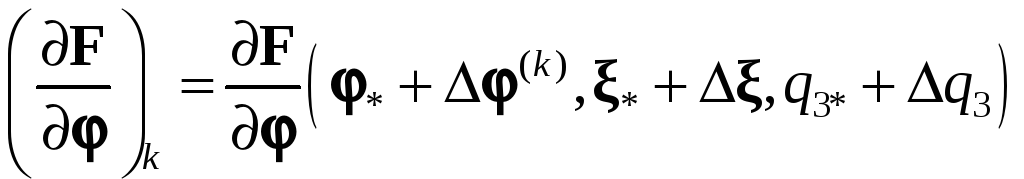представляет собой матрицу Якоби для системы (2.11).

Для рассмотренных групповых уравнений

;

. (2.12)

. (2.15)

Определитель этой матрицы (якобиан) определяется выражением

. (2.16)

На рис. 2.8 дана условная геометри­ческая интерпретация метода Ньютона, относящаяся к случаю, когда векторы и – одномерные.

Для того, чтобы избежать многократного вычисления матрицы , обратной матрице Якоби, можно пользоваться модифицированным методом Ньютона (методом секущих), при котором используется процедура, соответствующая формуле

k = 1, 2, … . (2.17)

где .

Положение механизма, близкое к исходному, не может быть получено описанным выше способом, если определитель матрицы Якоби обращается в ноль. Это – особое (сингулярное) положение группы АВСD.

Рис.

П

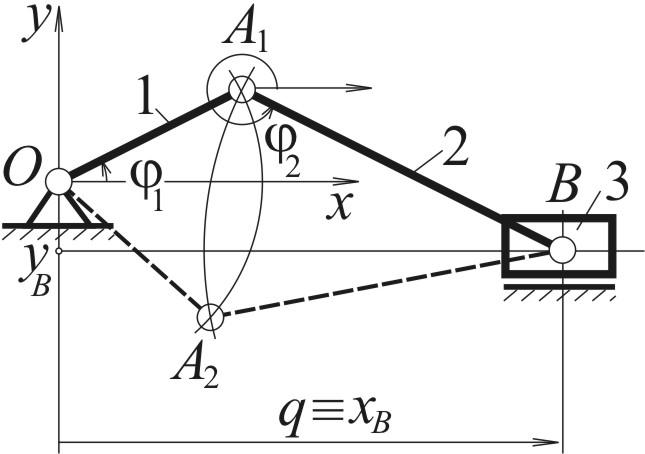ример с ползунно-кривошипным механизмом.

Вход q  x_B.

В механизме две структурные группы:

• однозвенная одноподвижная (ползун 3)

• двухзвенная группа Ассура типа ВВВ (звенья 1 и 2).

Такой механизм при одном значении q может принимать две различные конфигурации: ОА₁В и ОА₂В, причем без разборки механизма.

Составим выражения для F:

,

где . Матрица Якоби:

.

Определитель матрицы Якоби (якобиан):

.

Отсюда видно, что якобиан обращается в 0 тогда, когда все три шарнира находятся на одной прямой (sin(₂ – ₁) = 0 – особое положение группы ВВВ).

Найдем обратную матрицу:

Тогда где , , k = 0,1,2, … . В особом положении (т.е. при sin(₂ – ₁) = 0) данный метод не работает.

а) б) в)

Билет №11. Кинематический анализ механизмов (плоских одноподвижных). Аналоги скоростей и ускорений. Примеры механизмов с внешним и внутренним входом.

Задачей кинематического анализа является определение скоростей и ускорений точек механизма, угловых скоростей и угловых ускорений его звеньев.

Синусный механизм.

Функция положения точки B:

.

Дифференцируя ее по времени, получим скорость точки В:

.

Продифференцировав по времени , получим ускорение точки В:

– аналог скорости или первая геометрическая передаточная функция;

– аналог ускорения или вторая геометрическая передаточная функция;

– обобщенная скорость; – обобщенное ускорение.

Для одноподвижного механизма (W = 1) функция положения:

x_М = П_х(q),. (2.18)

Дифференцируя (2.18) по времени, получим:

, (2.19)

Для определения ускорения точки М продифференцируем выражение (2.19) по времени:

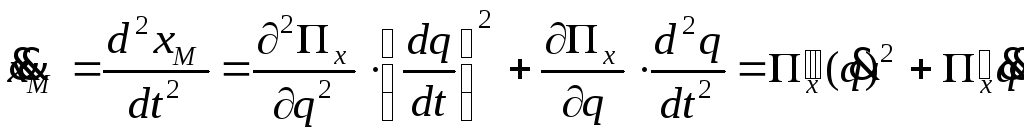, (2.20)

При = const, = 0 .

Пример. Механизм с внутренним входом.

Структура – одна трехзвенную одноподвижную структурную группу.

Групповые уравнения:

(2.21)

Продифференцируем (2.21) по обобщенной координате q:

(2.22)

Аналоги угловой скорости первого и второго звена:

Нетрудно видеть, что относительно аналогов скорости система уравнений (2.22) является линейной:

(2.22′)

Отсюда несложно найти аналоги скорости:

(2.23)

(2.24)

Знаменатель выражений (якобиан) обращается в ноль при ₁=₃  n, n=0, 1, … . В этих случаях механизм попадает в особые положения (рис. 2.11, б), а аналог скорости .

(2.22)

Продифференцируем (2.22) по обобщенной координате q:

(2.25′)

– аналог кориолисова ускорения,

, – аналоги вращательных составляющих ускорений,

, – аналоги центростремительных составляющих ускорений.

Аналоги угловых ускорений и :

(2.26)

(2.27)

При приближении к особому положению аналоги ускорений и .

Билет №12. Кинематический анализ многоподвижных механизмов. Пример для двухподвижного механизма.

Многоподвижные механизмы. Функция положения:

х_М = П_х(q₁, q₂, … , q_W). (2.28)

Скорость точки М:

. (2.29)

Ускорение точки М:

(2.30)

Пример двухподвижного механизма .

Функции положения:

2.31)

В дальнейшем удобно представить (2.31) в более краткой форме:

(2.31′)

Возьмем производную от (2.31′) по обобщенной координате q₁:

(2.32)

Производные и :

(2.33)

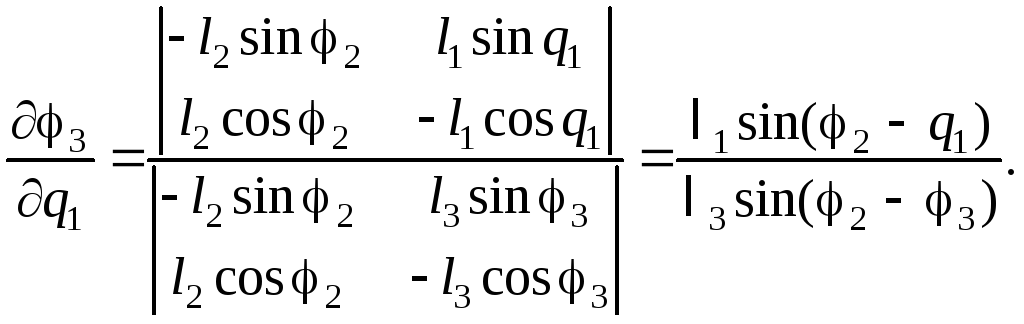(2.34)

(2.31′)

Далее продифференцируем (2.31′) по обобщенной координате q₂:

(2.35)

Частные производные по q₂:

(2.36)

(2.37)

Особое положение в механизме наступит тогда, когда , т.е. при .

Для того, чтобы найти вторые частные производные и , можно продифференцировать по q₁ выражения (2.33) и (2.34). Аналогично для отыскания производных и надо продифференцировать по q₂ выражения (2.36) и (2.37).

Для того, чтобы найти смешанные производные и , надо продифференцировать выражения (2.32) по q₂ или (2.35) по q₁, например:

(2.38)

Из системы (2.38) можно получить смешанные производные и .

Билет №13. Геометрический анализ исполнительных механизмов промышленных роботов.

Пространственный механизм со структурой «дерева».

О_sx_sy_sz_s – связана со звеном s, О_s-1x_s-1y_s-1z_s-1 – связана со звеном s-1

Таблица косинусов

Таблица 2.1

	xs	ys	zs
xs-1	cos(xs-1,xs)	cos(xs-1,ys)	cos(xs-1,zs)
ys-1	cos(ys-1,xs)	cos(ys-1,ys)	cos(ys-1,zs)
zs-1	cos(zs-1,xs)	cos(zs-1,ys)	cos(zs-1,zs)

Обычно для краткости эти косинусы обозначают буквами  (табл. 2.2):

Таблица 2.2

	xs	ys	zs
xs-1	11	12	13
ys-1	21	22	23
zs-1	31	32	33

• Сумма квадратов косинусов в каждой строке равна единице, т.е.

²₁₁ + ²₁₂ + ²₁₃ = 1;

²₂₁ + ²₂₂ + ²₂₃ = 1;

²₃₁ + ²₃₂ + ²₃₃ = 1;

• Сумма попарных произведений равна 0, т.е.

₁₁ ₂₁+ ₁₂₂₂ + ₁₃₂₃ = 0;

₂₁ ₃₁+ ₂₂₃₂ + ₂₃₃₃ = 0;

₁₁ ₃₁+ ₁₂₃₂ + ₁₃₃₃ = 0.

Матрица направляющих косинусов А_s-1,s

. (2.39)

А_s-1,s+1 = А_s-1,s А_{s,s+1 .} (2.40)

. (2.41)

Вектор в (s–1)-й системе координат: . (2.42)

Вектор в s-й системе координат: . (2.43)

Вектор в (s–1)-й системе координат: 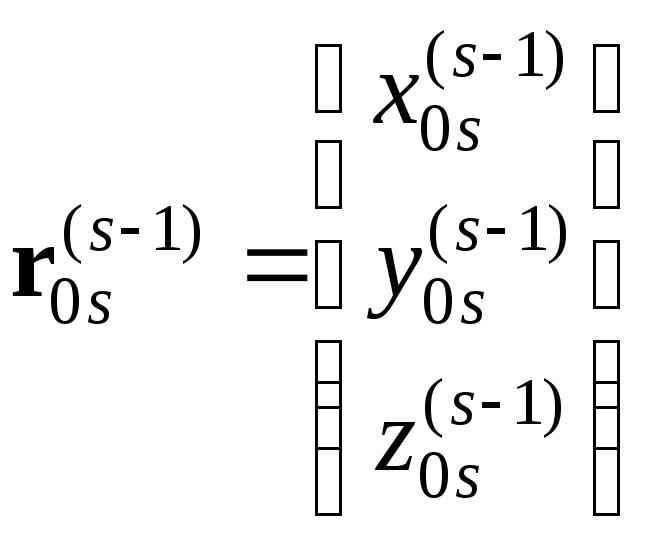. (2.44)

Выражение (2.41) в проекциях на оси (s–1)-й системы координат:

. (2.45)

Четырехмерные векторы-столбцы координат:

, . (2.46)

Блочные матрицы 4х4 (матрицами перехода от s-й системы координат к (s–1)-й системе):

. (2.47)

Вместо

. (2.45)

записываем

(2.48)

Перемножая последовательно матрицы перехода, можно дойти до неподвижной системы координат:

. (2.49)

– вектор-столбец координат точки М в системе, связанной со звеном n,

– вектор-столбец координат точки М в неподвижной системе.

Билет №14. Матрица преобразования координат (матрица перехода) для вращательной КП. Пример.

1. Матрица перехода во вращательной кинематической паре.

q_s – угол поворота s-го звена относительно (s–1)-го.

Oz_s совпадает с осью вращения во вращательной КП.

O_s^*х_s^*у_s^*z_s^* – начальное положение O_sх_sу_sz_s (при q_s=0).

Матрица направляющих косинусов А_s-1,s :

. (2.50)

Матрица А_s-1,s*(0) является постоянной.

Составим таблицу направляющих косинусов для A_s*,s(q_s) .

Таблица 2.3

	xs	ys	zs
xs*	cos(qs)	cos(qs+/2)	cos(/2)
ys*	cos(3/2+qs)	cos(qs)	cos(/2)
zs*	cos(/2)	cos(/2)	cos(0)

Тогда матрица А_s*,s(q_s) равна:

. (2.51)

Матрица P_z(q_s) называется матрицей поворота.

Матрица перехода во вращательной кинематической паре:

. (2.52)

Билет №15.Матрица преобразования координат (матрица перехода) для поступательной КП. Пример.

2. Матрица перехода в поступательной кинематической паре.

q_s – поступательное перемещение звена s относительно звена (s–1).

Oх_s совпадает с линией относительного перемещения звеньев s и (s–1).

O_s^*х_s^*у_s^*z_s^* – начальное положение O_sх_sу_sz_s (при q_s=0). (2.53)

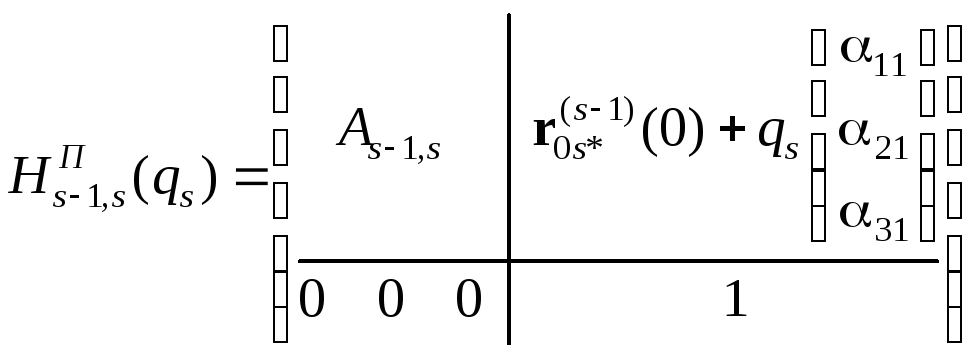
. (2.54)

Пример.

Степень подвижности:

W=63-53=3.

Обобщенные координаты:

q₁, q₂, q₃.

O₁x₁y₁z₁, O₂x₂y₂z₂, O₃x₃y₃z₃ – связаны с 1,2,3 звеньями соответственно.

Начальные положения каждой из систем координат:

O₁^*x₁^*y₁^*z₁^*, O₂^*x₂^*y₂^*z₂^*, O₃^*x₃^*y₃^*z₃^*.

O₁^*x₁^*y₁^*z₁^* совпадает с неподвижной системой Ox₀y₀z₀.

a, b, c – конструктивные параметры.

Построить функцию положения точки М:

Решение.

.

.

Составим матрицы перехода.

Для составления матрицы А₁₂ построим табл. 2.4 направляющих косинусов:

Таблица 2.4

	x2	y2	z2
x1	0	0	1
y1	0	–1	0
z1	1	0	0

Тогда матрица перехода

.

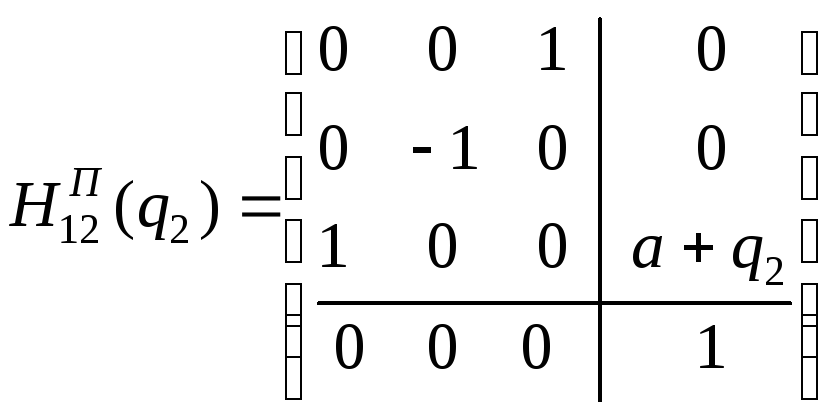Для построения матрицы А_23*(0) составим табл. 2.5 направляющих косинусов:

Таблица 2.5

	x3*	y3*	z3*
x2	0	1	0
y2	–1	0	0
z2	0	0	1

Найдем матрицу перехода :

Подставляя найденные матрицы перехода, получим:.

Билет №16. Кинематический анализ исполнительных. Механизмов промышленных роботов.

Задачей кинематического анализа является определение скоростей и ускорений точек механизма и угловых скоростей и угловых ускорений его звеньев.

(2.55)

(2.56)

В выражения (2.55) и (2.56) входят первые и вторые частные производные от матриц перехода.

, (2.57)

где .

, (2.58)

где .

= const . (2.59)

. (2.60)

Определение угловых скоростей.

, m=1, … n. (2.61)

– вектора угловых скоростей в неподвижной системе координат,

– вектор относительной угловой скорости звена m относительно (m–1).

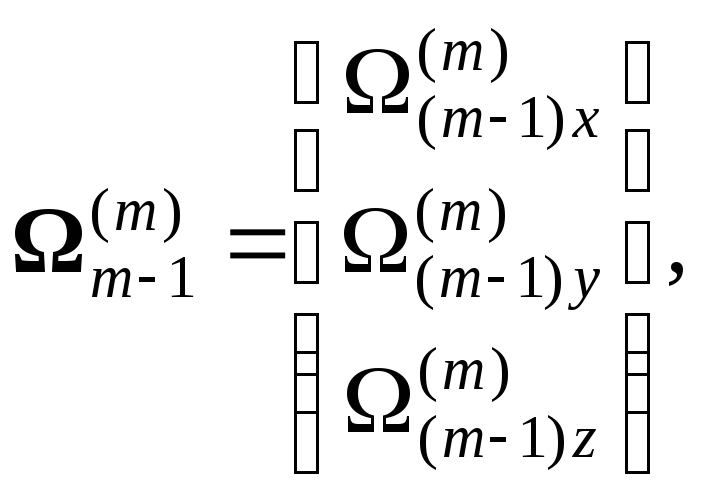
. (2.62)

В проекциях на оси (m–1)-й системы координат:

. (2.63)

. Отсюда . (2.64)

, m=1, … n. (2.65)

Определения угловых ускорений.

. (2.66)

– абсолютная производная по времени от вектора, – относительная производная по времени от вектора.

продифференцируем (2.61) по времени. При этом учтем, что абсолютная производная по времени от вектора равна геометрической сумме относительной производной того же вектора и векторного произведения вектора угловой скорости вращения относительной системы координат на дифференцируемый вектор:

. (2.66)

. (2.67)

В проекциях на оси (m–1)-й системы координат:

, m=1, … , n . (2.68)

.

В соответствии с условленным ранее правилом выбора осей локальной системы координат во вращательной кинематической паре вектор-столбец проекций углового ускорения на оси m-й системы координат представляет собой:

.

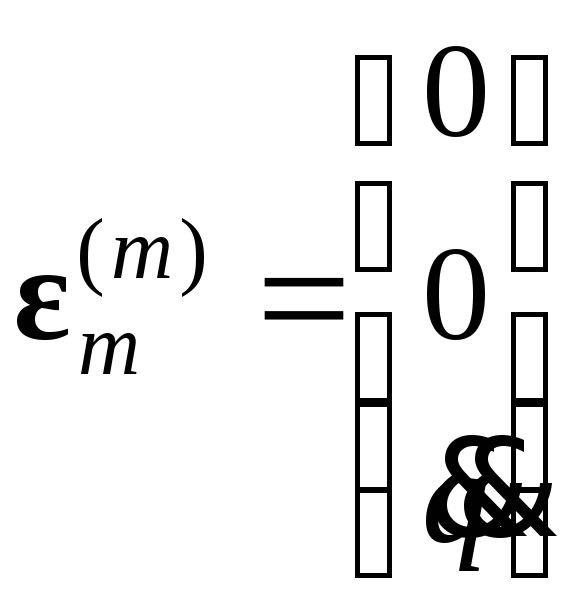Проецируя (2.67) на оси m-й системы координат и используя соотношение , получим следующее выражение для рекуррентной процедуры отыскания угловых ускорений:

, m=1, … , n . (2.68)

Пример определения угловых скоростей и ускорений.

;;;;;.

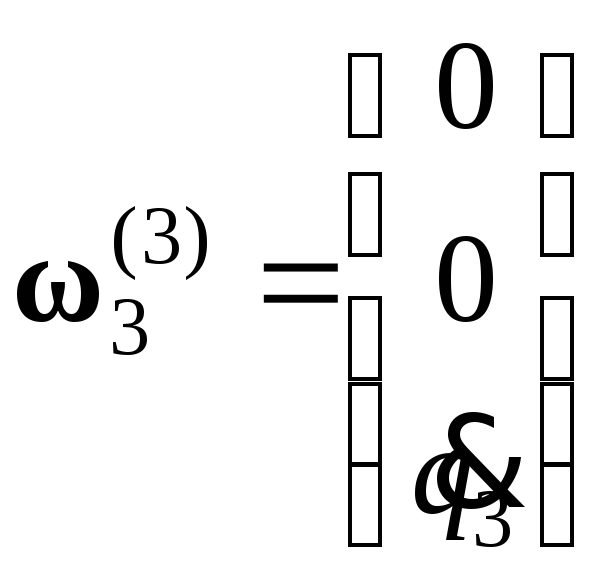Угловые скорости m = 1,2,3:

;

;

.

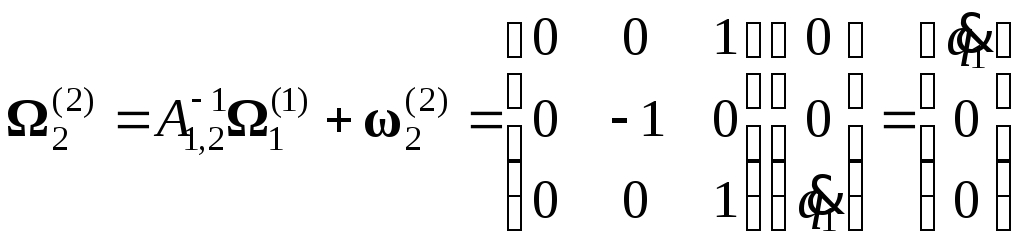Угловые ускорения:

;

;

Билет №17. Механизмы с линейной функцией положения. Фрикционные передачи. Ременные передачи. Цепные передачи.

Функции положения:

, (3.39)

где φ и q – соответственно выходная и входная координаты, b, i – постоянные. Механизмы с линейной функцией положения обычно называют передачами. . (3.40) i –передаточное отношение.

1. Фрикционные – передачи, в которых движение передается за счет сил трения между звеньями (frictio по-латыни – трение).

(3.41)

. (3.41)

(3.42)

Точка К – мгновенный центр скоростей в относительном движении.

r_1, r₂ –подвижные центроиды (катятся друг по другу без скольжения).

Фрикционные передачи не передают большие усилия.

Ременные передачи.

1 – ведущий шкив 1, 2 – ведомый шкив, 3 – ремнь. Соотношение для угловых скоростей ведущего и ведомого шкивов: .

Межосевое расстояние а=О₁О₂ больше, чем во фрикционных.

Направление вращение у ведущего и ведомого колес совпадает.

Бидет № 18. Зубчатые передачи. Зубчатые ряды.

2. Зубчатые передачи.

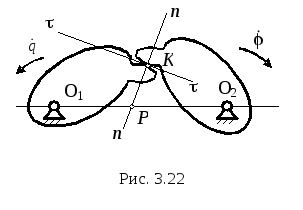Р – полюсом зацепления (мгновеннй центр скоростей в относительном движении)

Относительная скорость в точке Р равна нулю, т.е. V_P1 = V_P2:

. (3.43)

Передаточное отношение i₁₂:

. (3.44)

Иными словами, нормаль, проведенная в точке контакта к сопряженным профилям, делит межосевое расстояние в отношении, обратно пропорциональном отношению угловых скоростей. Это – основная теорема зацепления. При i₁₂=const O₁P=const, O₁P=const

В этом случае центроидами в относительном движении являться начальныме окружности ( r_w1,r_w2 ).

Передаточное отношение для внешнего зацепления:

. (3.44′)

,

Начальное межосевое расстояние

а_w = r_w1 + r_w2. (3.45)

. (3.46)

Передаточное отношение для внутреннего зацепления:

. (3.44″)

,

Начальное межосевое расстояние а_w = r_w2 – r_w1. (3.47)

. (3.48)

Передаточное отношение для зубчато-реечной передачи:

(3.49)

Конические колеса – передача вращения между валами с пересекающимися осями

Мгновенная ось вращения в относительном движении (OP) – геометрическое место точек тел, имеющих в данный момент нулевую относительную скорость.

Подвижные аксоиды (начальные конусы) – поверхности, образованные мгновенной осью в локальной системе координат, связанной со звеном 1 или 2).. (3.50)

Передаточное отношение: . (3.51)

Поскольку r_w1 = OPsin₁, r_w2 = OPsin₂ , то (3.52)

В ортогональных передачах (угол между осями  = 90⁰⁾:

i₁₂ = ctg ₁ = tg ₂ . (3.53)

Гиперболоидные передачи (передача вращения между валами, оси которых скрещиваются).

Нет ни мгновенного центра скоростей в относительном движении, ни мгновенной оси.

Относительное движение можно представить как поворот вокруг некоторой оси и скольжение вдоль нее (мгновенная винтовая ось).

Винтовые аксоиды относительного движения –однополостные гиперболоиды вращения.

Упрощение:

• части 1 гиперболоидов заменяют цилиндрическими поверхностями и получают винтовые зубчатые передачи;

• части 2 заменяют коническими поверхностями и получают гипоидные зубчатые передачи.

В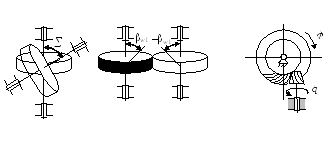интовые зубчатые передачи гипоидные зубчатые передачи .

Угол  между скрещивающимися осями .

Если ₁ = – ₂, то  = 0, и оси колес оказываются параллельны.

Нормальные составляющие скоростей точек контакта первого и второго колеса должны быть равными, то есть V_n1=V_n2, то V₁ cos _w1=V₂ cos _w2. Учитывая, что V₁=, а , передаточное отношение винтовой передачи:

. (3.54)

Червячная передача - частный случай гиперболоидной зубчатой передачи .

Угол скрещивания осей в большинстве случаев равен 90⁰. 1 – червяк (z₁ число заходов),

2 – червячное колесо (z₂ ).

, (3.55)

. (3.56)

Передаточное отношенияе червячной передачи:

. (3.57)

3. Ряды зубчатых колес. Передаточное отношение обратно пропорционально отношению радиусов начальных окружностей колес.

В инженерной практике по конструктивным соображениям это отношение не превышает 5 … 7. Для получения большего передаточного отношения зубчатые колеса составляют в ряды зубчатых колес).

Передаточное отношение такого ряда :

,

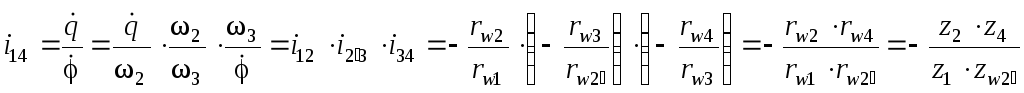r_w3 – паразитное колесо .

Билет № 19. Коробка передач. Коробка скоростей. Коробка подач. Пример: четырёхскоростная коробка передач.

1. Коробки передач.

а) два фиксированных значения передаточного отношения:

(i_I-II)₁ = z₂ / z₁, (i_I-II)₂ = z₄ / z₃.

б) пять значений передаточного отношения:

, , , , .

Билет № 20. Вариаторы цепные и ременные. Вариаторы торовые.

1. Вариаторы. Плавное изменение передаточного отношения. осуществляют с помощью передачи, называемой вариатором.

Б и в
Рис. 3.31

Для примера рассмотрим вариаторы CVT (Continuously Variable Transmission), применяемые в автомобилестроении.

В торовом вариаторе Toroidal CVT вместо гибкого звена используются ролики.

Передаточное отношение вариатора i₁₂:

где r_в – радиус огибающей профилей звеньев 1 и 2; φ – угол отклонения звена 4 от нейтрального положения; α – параметр вариатора: sin α = r_р / r_в ; r_р = d_р / 2 – радиус ролика 3.

В нейтральном положении φ = 0, d₁ = d₂, i₁₂ = 1, ω₁ = ω₂.

При φ > 0 (как на рис. 3.32) d₁ < d₂, i₁₂ > 1, ω₁ > ω₂ (понижающая передача).

При φ < 0 d₁ > d₂, i₁₂ < 1, ω₁ < ω₂ (повышающая передача).

К недостаткам вариаторов относят ограничение по передаваемой мощности, из-за чего их не используют в грузовых автомобилях.

Билет № 21. Кинематика планетарных механизмов. Примеры.

Планетарными механизмами называют зубчатые механизмы с подвижными осями колес.

z₁, z₃ – центральные или солнечные колеса,

z₂ – сателлит (или планетное колесо),

H – водило.

Число степеней подвижности механизма (формулу Чебышева):

,

N=4 – число подвижных звеньев,

р_н=4 – число низших кинематических пар,

р_в=2 – число высших кинематических пар.

Планетарные механизмы с неподвижным зубчатым колесом называют эпициклическими.

В планетарных механизмах уже нельзя использовать формулы, полученные для определения передаточного отношения ряда зубчатых колес, т.е.

.

Определение передаточного отношения.

Методом обращения движения: всем звеньям механизма, включая стойку, сообщается угловая скорость, равная угловой скорости водила _н и направленная в противоположную сторону.

В таком обращенном механизме водило оказывается неподвижным.

. (3.59)

Здесь – передаточное отношение от первого колеса к третьему при неподвижном водиле Н, т.е. в системе координат, связанной с водилом.

– знак «минус» при внешнем зацеплении,

– знак «плюс» при внутреннем зацеплении

Пример. Редуктор Давида.

Колесо с числом зубьев z₄ неподвижное.

Числа зубьев: z₁=z₃=100, z₂=101, z₄=99.

Передаточное отношение от водила Н к колесу:

.

Учитывая, что ₄ = 0, найдем отношение (т.е. при неподвижном четвертом колесе):

,

т.е. для того, чтобы первое колесо сделало один оборот, надо повернуть водило 10 000 раз. Обычно передаточное отношение в планетарных механизмах не превышает 150.

Хотя на кинематических схемах обычно изображают один сателлит, в реальных конструкциях их устанавливают несколько. Это делается для уменьшения нагрузки на колеса и для уравновешивания центробежных сил инерции. При этом следует следить за тем, чтобы один сателлит не накладывался на другой, т.е. чтобы выполнялось условие соседства: расстояние между осями двух соседних сателлитов (рис.3.32) должно быть больше диаметра окружности их вершин:

,

где – радиус окружности вершин сателлита. Пусть k – число сателлитов. В равнобедренном треугольнике 0А₁А₂ :

,

где – радиусы начальных окружности соответственно центрального колеса и сателлита. Тогда условие соседства можно записать в виде:

.

В частном случае при использовании несмещенных колес (о них пойдет речь ниже) , где – числа зубьев центрального колеса и сателлита. Для несмещенных колес условие соседства записывают в виде:

.

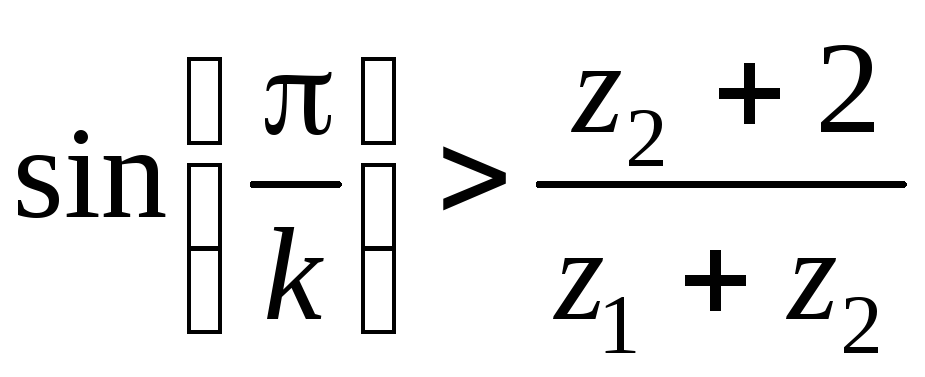Сателлиты размещают равномерно, т.е. соблюдением углового шага . Поскольку каждое вновь устанавливаемое колесо должно входить в зацепление с уже установленными колесами, то должно выполняться еще одно соотношение между числами зубьев колес и числом сателлитов, так называемое условие сборки (условие монтажа). Приведем его без вывода для несмещенных колес:

,

где k – число сателлитов, – число зубьев центрального колеса с внешним зубчатым венцом, – число зубьев колеса с внутренним зубчатым венцом, n – целое число.

Пример. Коробока передач.

1-я передача. М1 и Т1 выключены, М2 и Т2 – включены: ω₁ = ω₃, ω_H2 = 0.

.

2-я передача. М1 и Т2 выключены, М2 и Т1 – включены: ω₁ = ω₃, ω₂ = ω₇ = ω₈.

< (i_I-II)₁.

3-я передача (прямая). М1 и М2 включены, Т1 и Т2 – выключены: ω₁ = ω₃ = ω₂. Тогда ω₁ = ω_H1 = ω_H2,

.

4-я передача (задний ход). М1 и Т2 включены, М2 и Т1 – выключены: ω₁ = ω₂, ω_H2 = 0.

< – 1.

В нейтральной передаче муфты М1 и М2 выключены.

Билет №22. Кинематика планетарной коробки передач.

Пример. Коробока передач.

1-я передача. М1 и Т1 выключены, М2 и Т2 – включены: ω₁ = ω₃, ω_H2 = 0.

.

2-я передача. М1 и Т2 выключены, М2 и Т1 – включены: ω₁ = ω₃, ω₂ = ω₇ = ω₈.

< (i_I-II)₁.

3-я передача (прямая). М1 и М2 включены, Т1 и Т2 – выключены: ω₁ = ω₃ = ω₂. Тогда ω₁ = ω_H1 = ω_H2,

.

4-я передача (задний ход). М1 и Т2 включены, М2 и Т1 – выключены: ω₁ = ω₂, ω_H2 = 0.

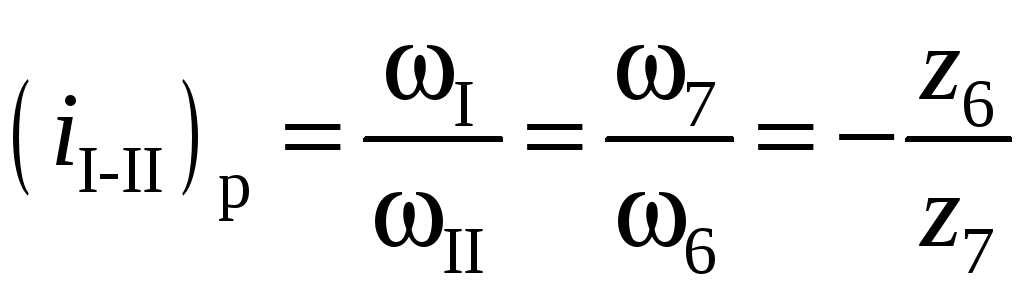< – 1.

В нейтральной передаче муфты М1 и М2 выключены.

Билет №23. Кинематика волновой передачи.

В последние годы появились механизмы, действие которых основано на деформации одного или нескольких звеньев. К таким механизмам относится волновая передача, предназначенная для передачи вращения через герметичную стенку, разделяющую пространства А и В (рис.3.35, а). Такая передача была придумана для космических спутников («космические технологии»). Все звенья передачи – жесткие, кроме колеса с числом зубьев z₁, которое называется гибким колесом. Конструктивно гибкое колесо выполнено в виде тонкостенного стакана, герметично соединенного со стенкой, разделяющей пространства А и В. Звено Н называется генератором волн. На генераторе Н закреплены ролики, которые прижимают гибкое колесо к жесткому колесу с числом зубьев z₂. При вращении генератора Н гибкое колесо, деформируясь под действием роликов, принимает форму овала и вызывает перемещение зубьев как гибкого колеса, так и жесткого колеса.

Таким образом, жесткое колесо, находясь в пространстве А, получает вращение от зубьев гибкого колеса, расположенных на внешней стенке стакана, в то время как генератор Н, вызывающий это движение зубьев, вращается внутри стакана. Передача называется волновой потому, что гибкое звено в целом остается неподвижным, но при вращении генератора по нему перемещается волна деформации, вызывающая небольшие перемещения зубьев.

Термины «гибкое звено», «тонкостенный стакан» не должны вводить в заблуждение: необязательно гибкое звено представляет собой нечто хлипкое и пластмассовое. Так, например, в волновом редукторе, выпускаемом новокраматорским машиностроительным заводом, гибкое колесо изготавливается из стали и имеет толщину 1535 мм.

Иногда удобнее оказывается делать неподвижным жесткое колесо, а гибкое колесо – подвижным выходным звеном (рис.3.35, б).

Рассмотрим кинематику волновой передачи.

Воспользуемся формулой Виллиса (3.61), учитывая, что у цилиндрических колес внутреннего зацепления направление вращения ведущего и ведомого колес совпадает:

(3.66)

При неподвижном гибком колесе z₁ (₁ = 0) получим:

. (3.67)

Пусть z₁ = 200, z₂ = 202; подставляя в (3.67), получим:

.

Таким образом, с помощью компактной волновой одноступенчатой передачи, имеющей всего два зубчатых колеса, можно получить такое же передаточное отношение, как и в трехступенчатом цилиндрическом редукторе, имеющем 6 зубчатых колес.

Билет № 24. Конические передачи. Автомобильный дифференциал.

Если r_w2  , то начальная окружность превращается в начальную прямую, а зубчатое колесо – в зубчатую рейку. В этом случае получают зубчато-реечную передачу (рис.3.23, в). Поскольку в полюсе зацепления относительная скорость равна 0, то V_P1=V_P2, и

(3.49)

Зубчатые колеса используют также и для передачи вращения между валами с пересекающимися осями (I и II на рис.3.24) – это конические колеса. Чаще всего угол между осями  = 90⁰ (такие передачи называют ортогональными), но возможны и другие углы. В передачах с коническими колесами существует мгновенная ось вращения в относительном движении (OP) – геометрическое место точек тел, имеющих в данный момент нулевую относительную скорость. Если мгновенную ось ОР, наклоненную к оси вращения I под углом ₁, вращать вокруг оси I, получится коническая поверхность – подвижная аксоида (поверхность, образованная мгновенной осью в локальной системе координат, связанной со звеном 1 или 2, называют подвижной аксоидой). Аналогично при вращении мгновенной оси ОР вокруг оси II получим коническую поверхность с половиной угла при вершине, равной ₂ (вторая подвижная аксоида). Подвижные аксоиды в теории зубчатых зацеплений называются начальными конусами. Зубья колес располагают вблизи начальных конусов, а поверхности вершин и впадин имеют коническую форму.

Поскольку подвижные аксоиды катятся друг по другу без скольжения, то

. (3.50)

Отсюда передаточное отношение i₁₂:

. (3.51)

Поскольку r_w1 = OPsin₁, r_w2 = OPsin₂ , то

. (3.52)

В ортогональных передачах:

i₁₂ = ctg ₁ = tg ₂ . (3.53)