Билет №1. Постановка задачи силового расчета. Силы, действующие в механизме. Уравнения движения системы. Кинематические пары, накладывающие идеальные связи.

В курсе теоретической механики рассматривались две задачи динамики:

1. Дан закон движения материальной точки известной массы; требуется найти силу, действующую на точку (первая задача динамики);

2. Дана сила, приложенная к материальной точке; требуется найти закон движения точки (вторая задача динамики).

В теории механизмов и машин также ставятся и решаются две задачи динамики. В частности, первая задача динамики: при известном (заданном) законе движения ведущего звена (ведущих звеньев) механизма требуется найти силы, действующие в механизме. Решение этой задачи называют силовым расчетом. Он имеет большое значение при проектировании машин и механизмов, особенно таких, которые передают большие усилия, т.к. найденные силы используются для дальнейших расчетов на прочность, жесткость и т.д., а также для выбора двигателя (двигателей).

Обычно при силовом расчете предполагается, что ведущее звено (звенья) совершают программное движение, необходимое для выполнения рабочего процесса. В дальнейшем законы движения могут уточняться в соответствии с результатами динамического анализа (решения второй задачи динамики), который будет рассматриваться далее.

При силовом расчете механизма считаются известными все активные силы, действующие на звенья механизма, кроме обобщенных движущих сил. К заданным активным силам относятся:

а) Рабочая нагрузка P – сила, действующая на рабочее звено при выполнении рабочего процесса. Например, сила резания в металлорежущем станке, силы сопротивления грунта, действующие на ковш экскаватора, силы давления воздуха на поршень компрессора и т.п. В некоторых случаях рабочая нагрузка представляет собой момент, например, момент электромагнитных сил, возникающих при вращении ротора электрического генератора, момент сил аэродинамического сопротивления, возникающих в роторных насосах, и т.д.

Рабочая нагрузка обычно не является постоянной. Часто она изменяется по мере перемещения рабочего звена. В этом случае может быть построена зависимость Р = Р(х), где Р – рабочая нагрузка, х – координата точки приложения нагрузки. В более сложных случаях нагрузка зависит также от скорости , ускорения и времени t: . Эти зависимости изучаются в специальных дисциплинах. При выполнении силового расчета они считаются заданными, но их следует привести к более удобному виду. Учитывая, что , , можно получить зависимость рабочей нагрузки от обобщенной координаты и ее производных:

. (4.1)

Если в механизме приложена не одна, а рабочих нагрузок, то для них задаются зависимостей:

, (m = 1, 2, … , ) . (4.2)

В многоподвижных механизмах координаты, скорости и ускорения точек приложения нагрузок зависят от всех обобщенных координат и их производных:

, (4.3)

где – функции положения.

Зная (4.3), можно получить зависимости рабочих нагрузок от обобщенных координат и их производных:

, (m = 1, … , ) . (4.4)

В дальнейшем будем предполагать, что рабочие нагрузки не зависят явно от времени и ускорений , поэтому выражения (4.4) будут представляться в форме:

, (m = 1, … , ) (4.5)

б) Cилы тяжести звеньев G_i, , где N – число звеньев. Эти силы являются постоянными, но точки их приложения, а, следовательно, и моменты сил тяжести относительно некоторых центров приведения изменяются в процессе движения.в) В некоторых механизмах используются пружины, обеспечивающие силовое замыкание кинетических пар (например, в кулачковых механизмах используются пружины, прижимающие толкатель к кулачку). Упругие силы, возникающие при деформации пружин, также являются активными. Их значение зависит от деформации пружин, т.е. от координат точек крепления концов пружины. При заданных законах движения эти силы могут быть определены в любой момент времени или в любом положении механизма.

Целью силового расчета является определение обобщенных движущих сил и реакций во всех кинематических парах. Обобщенные движущие силы – это обобщенные силы, которые необходимо приложить к входным звеньям механизма для того, чтобы получить заданное программное движение при выполнении рабочего процесса. Определив движущие силы, можно выбрать двигатели, приводящие в движение машину.

Реакции в кинематических парах – пассивные силы; как правило, это силы, распределенные по поверхностям соприкосновения конструктивных элементов, образующих пару. Однако в рамках физических моделей кинематических пар, рассматриваемых в курсе теории механизмов и машин, вообще говоря, невозможно определить законы распределения реакций по поверхностям элементов. Поэтому мы ограничимся определением главных векторов и главных моментов сил реакций в каждой кинематической паре.

Рассмотрим вращательную кинематическую пару (рис.4.1); главный вектор сил реакций и главный момент определяются заданием шести скалярных величин – их проекций на оси системы 0xyz.Определим общее число неизвестных, подлежащих определению при силовом расчете. Пусть механизм имеет w число степеней подвижности и p кинематических пар. Тогда число неизвестных обобщенных движущих сил равно w, а число неизвестных компонент реакций – 6p. Таким образом, общее число неизвестных

n_u = w + 6p = w + 6p₁ + 6p₂ + 6p₃ + 6p₄ + 6p₅ . (4.6)

Эти неизвестные могут быть определены решением уравнений движения звеньев механизма. Пусть число звеньев равно N. Для каждого подвижного звена можно составить два векторных уравнения движения на основе теорем об изменении количества движения и кинетического момента. Если – вектор количества движения s–го звена, а – его кинетический момент, то уравнения движения записываются в виде:

(4.7)

где – внешние силы, действующие на s–е звено, – радиусы-векторы точек их приложения, g_s – число сил, приложенных к s–му звену. Как известно из курса теоретической механики, другие независимые уравнения движения для твердого тела составить невозможно. Общее число векторных уравнений (4.7) равно 2(N–1); проецируя их на оси координат, получаем 6(N–1) скалярных уравнений.Пусть механизм не содержит избыточных связей. Тогда для него справедлива формула

(4.8)

где p_s– число s–подвижных пар. Из уравнения (4.8) можно выразить число уравнений n_eq = 6(N–1):

.

Сравнивая число неизвестных n_u и число уравнений n_eq , имеем:

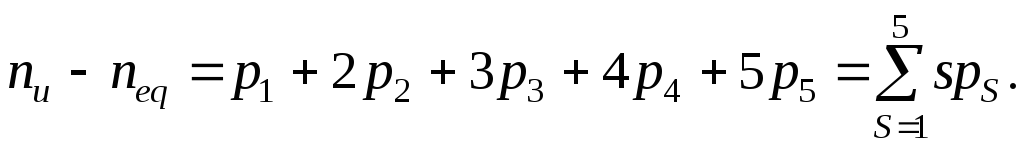(4.9)

При такой постановке задачи силового расчета число неизвестных всегда больше числа уравнений, что делает эту задачу неразрешимой. Она тем более неразрешима, если в механизме имеются избыточные связи, поскольку при этом число неизвестных реакций возрастает, а число уравнений остается неизменным.

Для того, чтобы задача стала разрешимой, необходимы дальнейшие уточнения физической модели, введение дополнительных предположений о свойствах кинематических пар. Одно из таких уточнений заключается в предположении о том, что все кинематические пары осуществляют идеальные связи. При идеальных связях работа сил реакций каждой кинематической пары должна равняться нулю при любом возможном перемещении, т.е. должно быть

(4.10)

Здесь – малые возможные перемещения вдоль осей координат, а – малые повороты вокруг этих осей. Вращательная пара (см. рис.4.1) допускает только малый поворот звена 2 (цапфы) относительно звена 1 (втулки) вокруг оси 0z. Тогда из (4.10) имеем

Поскольку при повороте , имеем Таким образом, одна из шести компонент реакций вращательной пары определилась, и число неизвестных уменьшилось на единицу – степень подвижности пары.

В поступательной паре возможное перемещение ползуна относительно направляющей направлено вдоль оси х. Поэтому здесь и поскольку имеем , что также определяет одну из неизвестных компонент реакций.

В цилиндрической паре отличны от нуля возможные перемещения (поворот вокруг продольной оси 0z) и (перемещение вдоль этой оси), так что здесь

В силу независимости возможных перемещений и это условие должно выполняться как при так и при . Это приводит к выводу о том, что R_Z и должны равняться нулю, что определяет для двухподвижной цилиндрической пары две компоненты реакций.

Аналогично можно показать, что в любой s–подвижной паре условие идеальности приводит к появлению s дополнительных соотношений для компонент реакций. В результате для механизма в целом появляется условий, что делает задачу силового расчета разрешимой. Часто в этом случае говорят о статической определимости механизма.

Билет №2 Уравнения кинетостатики

Уравнения (4.7) удобно представить в другой форме. Введем в рассмотрение силы инерции материальных точек s–го звена

(4.11)

где – масса i–й материальной точки; – ее ускорение. Напомним, что «сила инерции» лишь условно называется силой; в действительности это мера движения материальной точки, подобная, например, количеству движения. Вводя силы инерции, можно преобразовать левые части уравнений (4.7); учитывая, что , получаем

(4.12)

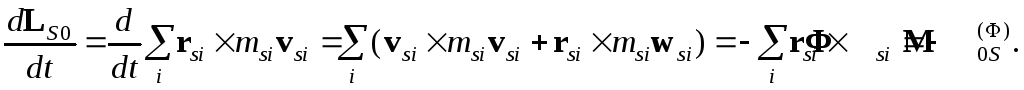(4.13)

Здесь – главный вектор сил инерции s–го звена, а – их главный момент относительно некоторой произвольно выбранной точки О.

В правых частях уравнений (4.7) выделим активные силы и реакции кинематических пар :

(4.14)

где и – главные векторы активных сил и реакций связей, действующих на s–е звено, и – их главные моменты относительно точки О. Подставив (4.14) в (4.7), получим уравнения движения в следующей форме:

. (4.15)

Уравнения движения получили форму уравнений равновесия. Можно сказать, исходя из этой формы, что активные силы, действующие на каждое из подвижных звеньев механизма, реакции связей и силы инерции звена образуют уравновешенную систему. Следует только помнить об условности такой формулировки; в действительности силы инерции силами не являются; они являются мерами движения. Соответственно уравнения (4.15) являются уравнениями движения, а не уравнениями равновесия. Чтобы подчеркнуть это обстоятельство, их называют уравнениями кинетостатики, а модель силового расчета механизма, основанную на их применении, – кинетостатической моделью.

Билет №3 Определение главного вектора и главного момента сил инерции (общий случай; поступательное движение; вращение вокруг неподвижной оси; плоское движение)

Уравнения (4.7) удобно представить в другой форме. Введем в рассмотрение силы инерции материальных точек s–го звена

(4.11)

где – масса i–й материальной точки; – ее ускорение. Напомним, что «сила инерции» лишь условно называется силой; в действительности это мера движения материальной точки, подобная, например, количеству движения. Вводя силы инерции, можно преобразовать левые части уравнений (4.7); учитывая, что , получаем

(4.12)

(4.13)

Здесь – главный вектор сил инерции s–го звена, а – их главный момент относительно некоторой произвольно выбранной точки О.

В правых частях уравнений (4.7) выделим активные силы и реакции кинематических пар :

(4.14)

где и – главные векторы активных сил и реакций связей, действующих на s–е звено, и – их главные моменты относительно точки О. Подставив (4.14) в (4.7), получим уравнения движения в следующей форме:

. (4.15)

Уравнения движения получили форму уравнений равновесия. Можно сказать, исходя из этой формы, что активные силы, действующие на каждое из подвижных звеньев механизма, реакции связей и силы инерции звена образуют уравновешенную систему. Следует только помнить об условности такой формулировки; в действительности силы инерции силами не являются; они являются мерами движения. Соответственно уравнения (4.15) являются уравнениями движения, а не уравнениями равновесия. Чтобы подчеркнуть это обстоятельство, их называют уравнениями кинетостатики, а модель силового расчета механизма, основанную на их применении, – кинетостатической моделью.

Для составления уравнений в форме (4.15) необходимо уметь определять главные векторы и главные моменты сил инерции звена при заданном законе его движения. Выражения для и в общем случае движения твердого тела выводятся в курсах аналитической механики. Пусть некоторая точка О (рис.4.2) выбрана за полюс звена, – вектор, определяющий положение его центра масс С.

Если известны ускорение полюса , вектор угловой скорости звена и вектор его углового ускорения (они определяются при кинематическом анализе механизма), то для главного вектора сил инерции и для главного момента их относительно точки О справедливы следующие выражения:

(4.16)

(4.17)

Здесь m – масса звена, I₀ – тензор инерции в точке О. Если ввести систему координат 0хyz, связанную со звеном, то тензор I₀ можно задавать матрицей моментов инерции

(4.18)

где J_X, J_Y, J_Z – осевые, а J_XY, J_YZ, J_XZ – центробежные моменты инерции. Найдем выражения для проекций на оси главного вектора и главного момента сил инерции в некоторых частных случаях.

a). Поступательное движение звена. Учитывая, что ω=0, ε=0, найдем :

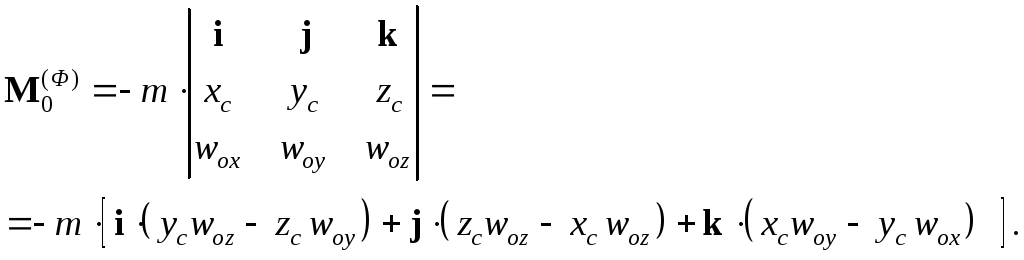
Здесь х_с, y_c, z_c – координаты центра масс. Тогда:

(4.19)

б). Вращение вокруг неподвижной оси (рис.4.3).

Здесь

ω_х = ω_y = 0; ω_z = ω; ε_x = ε_y = 0; ε_z = ε; w₀ = 0.

Для определения главного вектора сил инерции найдем векторные произведения:

,

.

Отсюда найдем проекции главного вектора сил инерции:

(4.20)

Для определения главного момента сил инерции найдем I₀ и :

Подставляя найденные соотношения в выражение (4.17), найдем главный момент сил инерции в проекциях на координатные оси:

(4.21)

в). Плоское движение звена. Выберем в качестве полюса центр масс звена С. Введем систему координат Сxyz так, чтобы ось Сz была перпендикулярна плоскости движения звена. В осях Cxyz построим тензор инерции I_С:

.

Тогда получим следующие выражения для главного вектора и главного момента сил инерции:

, (4.22)

Билет №4,5. Силовой расчет плоских рычажных механизмов (одноподвижных и многоподвижных). Примеры.

4.3. Решение уравнений кинетостатики

Для механизмов с идеальными связями уравнения кинетостатики представляют собой систему линейных алгебраических уравнений, обладающую единственным решением, если избыточные связи в системе отсутствуют, а рассматриваемое положение механизма не является особым. Для сложных механизмов, содержащих большое число подвижных звеньев, система уравнений кинетостатики имеет высокий порядок (для N–1 подвижных звеньев – 6ּ(N–1) уравнений). Ее решение существенно облегчается тем, что она может быть разделена на несколько независимых систем, каждая из которых содержит обобщенную движущую силу и реакции кинематических пар, действующие на звенья одной структурной группы. Действительно, для каждой структурной группы, не содержащей избыточных связей, справедлива структурная формула

(4.23)

где w_G – число степеней подвижности группы, N_G – число подвижных звеньев группы, p_SG – число s-подвижных кинематических пар в группе. С другой стороны, как было показано выше, сумма

(4.24)

представляет собой число неизвестных движущих сил и реакций в идеальных связях, подлежащих определению. Сравнивая выражения (4.23) и (4.24), замечаем, что n_u=6N_G, т.е. число неизвестных сил равно числу уравнений кинетостатики. Таким образом, уравнения кинетостатики могут решаться последовательно для каждой структурной группы.

Силовой расчет следует производить в направлении, обратном геометрическому и кинематическому расчетам, т.е. начинать его с групп последнего слоя. Тогда реакции во внешних кинематических парах групп m–го слоя оказываются известными и могут рассматриваться как заданные силы при расчете групп (m–1)-го слоя.

Особенности расчета плоского механизма. В плоском механизме, выделяя последовательно плоские структурные группы, можно для каждой из них определить отдельно компоненты реакций, лежащих в плоскости движения х0y (R_x, R_y, ), и обобщенные движущие силы. Компоненты реакций, не лежащие в плоскости движения, входят в другую группу уравнений. Часто из-за наличия избыточных связей определение всех реакций второй группы (Rz, , ) становится невозможным; в этом случае приходится ограничиваться определением только реакций освобождающих связей.

Рассмотрим некоторые примеры.

а) На рис.4.4 показан плоский механизм с одной степенью подвижности, состоящий из двух структурных групп: однозвенной одноподвижной группы (звено 1) и группы Ассура типа ВВП (звенья 2 и 3).

На рисунке нанесены активные силы: заданные и подлежащие определению (движущий момент Q), а также силы инерции, лежащие в плоскости движения , и проекции моментов сил инерции на ось z, перпендикулярную плоскости движения (). Силовой расчет начинается с последней группы, т.е. группы Ассура ВВП (рис.4.5, а). В соответствии с принципом освобождаемости от связей в шарнире А и в ползуне В приложены реакции отброшенных связей. На рисунке показаны компоненты реакций, лежащие в плоскости движения. Во вращательных парах (например, в шарнире А) возникают реакции с компонентами R_x и R_y, а в поступательных парах (например, в поступательной паре В) – нормальная реакция R и момент . Каждая компонента реакций снабжена двумя индексами, указывающими номер воздействующего звена и номер звена, воспринимающего воздействие. Следовательно, в шарнире А со стороны звена 1 на звено 2 действуют компоненты реакции R_12x и R_12y, а в поступательной паре В со стороны стойки 0 на ползун 3 действуют реакция R₀₃ и момент .

Реакция в шарнире В является внутренней для группы, поэтому она на рисунке не показана. Для того, чтобы включить в рассмотрение реакцию в шарнире В, надо отбросить либо звено 2, либо звено 3. На рис.4.5, б оставлено звено 3 (ползун); к указанным ранее силам добавлены компоненты реакции R_23x и R_23y, действующей со стороны звена 2 на звено 3.

Таким образом, в группе ВВП в плоскости, перпендикулярной оси z, всего 6 неизвестных: R_12x, R_12y, R_23x, R_23y, R₀₃, . Для плоской двухзвенной группы можно составить 6 независимых уравнений кинетостатики. В некоторых случаях удается так составить уравнения, чтобы в них было по одному неизвестному. Например, для звена 3 из условия равенства нулю суммы моментов всех сил относительно оси Bz (т.е. оси z, проходящей через точку B) следует: .

Сумма моментов всех сил, действующих на звенья 2 и 3, относительно оси Аz:

(Р + Ф₃)(y_A – y_B) – (R₀₃ – G₃)(x_A – x_B) + Ф_2x(y_A – y_S2) –

– (Ф_2y – G₂)(x_A – x_S2) + = 0,

где Ф_2х и Ф_2y – проекции главного вектора сил инерции второго звена, х_А, y_A, x_B, y_B, x_S2, y_S2 – координаты точек соответственно А, В, S₂. Отсюда можно найти реакцию R₀₃. После этого легко определяются остальные неизвестные. Уравнения для ползуна 3:

R_23x + P + Ф₃ = 0,

R₀₃ + R_23y – G₃ = 0.

Уравнения для звеньев 2 и 3:

R_12x + Ф_2x + P + Ф₃ = 0;

R_12y + Ф_2y – G₂ + R₀₃ – G₃ = 0.

После определения всех реакций в группе ВВП переходят к расчету первой структурной группы (рис.4.6).

Реакции в шарнире А уже известны: в соответствии с третьим законом Ньютона R_12x=–R_21x, R_12y=–R_21y. Следовательно, остаются три неизвестные: компоненты реакции R_01x, R_01y в шарнире 0 и движущий момент Q. Для кривошипа можно составить три уравнения кинетостатики, из которых находятся оставшиеся неизвестные. Если угловая скорость вращения кривошипа постоянна и центр масс находится на оси вращения О, то уравнения кинетостатики можно записать в виде:

R_21x + R_01x = 0,

R_21y + R_01y – G₁ = 0,

R_21x(y₀ – y_A) – R_21y(x₀ – x_A) + Q = 0.

Последовательность силового расчета проиллюстрирована на схеме рис.4.7. Предварительно определяются силы инерции . Потом решаются 6 уравнений для звеньев 2 и 3 группы ВВП, входящей во второй слой, находятся реакции R_12x, R_12y, R_23x, R_23y, R₀₃, . Затем решаются три уравнения для звена 1, являющегося группой первого слоя. Реакции R_21x и R_21y рассматриваются как известные (R_12x = – R_21x, R_12y = – R_21y). Определяются реакции R_01x, R_01y и движущий момент Q.

б) Механизм с тремя степенями подвижности (рис.4.8). Данный механизм состоит из трех одноподвижных групп: двух однозвенных (звенья 1 и 5) и одной трехзвенной (звенья 2, 3, 4). Определив силы инерции и моменты сил инерции звеньев, а также задав значения активных сил P_3X и P_3Y, приложенных в точке С₃ звена 3, и момента М^w, приступаем к силовому расчету последней структурной группы АВСD. Для плоской системы сил, действующих на три звена этой группы, составляем 9 уравнений кинетостатики, из которых определяем обобщенную движущую силу Q₂ и 8 реакций (R_12X, R_12Y, R_23X, R_23Y, R_34X, R_34Y, R_54X, R_54Y). Затем приступаем к расчету однозвенных групп первого слоя ОА и ЕD. При этом силы R_21X = – R_12X, R_21Y = – R_12Y, R_45X = – R_54X, R_45Y = – R_54Y рассматриваются уже как известные, найденные на предыдущем этапе. Из уравнений кинетостатики для звена ОА определяем R_01X, R_01Y и обобщенную движущую силу Q₁; из уравнений, составленных для звена ЕD, определяем R_05X, R_05Y и обобщенную движущую силу Q₃.

Н а рис.4.9 схематично представлен алгоритм силового расчета этого механизма. Для каждой группы указаны заданные («входные») силы и силы, найденные при силовом расчете.

Рис. 4.9

Силовой расчет по кинетостатической модели может производиться не только решением уравнений кинетостатики, составленных для каждого звена в отдельности, но и с помощью других методов. Рассмотрим, каким образом можно провести расчет трехзвенной группы АВСD, показанной на рис.4.8, методом размыкания кинематической цепи. Разомкнем кинематическую цепь в шарнире D и введем реакции освобождающих связей R_54X и R_54Y. Составим уравнения равновесия моментов всех активных сил, всех сил инерции и введенных реакций связей относительно осей шарниров А, В, С. Получим три уравнения:

Из этих уравнений определяются три неизвестные величины: R_54X, R_54Y и Q₂. После этого определение реакций в шарнирах А, В, С не вызывает затруднений; их можно найти, например, из уравнений проекций на оси х и y сил, действующих на звенья 2, 3, 4.

Решение уравнений кинетостатики усложняется, если в механизме имеются избыточные связи. В этом случае система становится статически неопределимой, поскольку число неизвестных реакций и движущих сил превосходит число уравнений кинетостатики. В ряде случаев удается избежать статической неопределимости увеличением подвижности некоторых кинематических пар (например, заменой вращательных пар цилиндрическими или сферическими); однако этот путь, связанный с изменением конструкции механизма, часто оказывается нежелательным как из-за снижения жесткости механической системы, так и по технологическим соображениям. В отдельных случаях оказывается возможным условно в расчетной схеме увеличить подвижность кинематических пар, учитывая некоторые свойства реальной конструкции. Так, например, наличие зазоров во вращательной паре (между осью шарнира и его втулкой) позволяет рассматривать при расчете эту пару как сферическую, считая равными нулю моменты, возникающие в ней при угловых перекосах. Однако в общем случае провести полный силовой расчет механизма с избыточными связями можно только за счет отказа от динамической модели жесткого механизма и введения расчетной схемы, учитывающей упругость звеньев и их соединений. Рассмотрение такой усложненной модели выходит за рамки дисциплины ТММ.

Вместе с тем всегда имеется возможность выполнить частичный силовой расчет механизма, ограничиваясь определением обобщенных движущих сил и реакций всех освобождающих связей. (Напомним, что освобождающей мы называем такую связь, устранение которой приводит к увеличению числа степеней подвижности механизма на единицу). Такой ограниченный расчет можно выполнить разными методами; один из них основан на использовании общего уравнения динамики.

Билет №6. Применение общего уравнения динамики для силового расчета механизмов (одноподвижных и многоподвижных). Пример с рычажным механизмом.

Для любой системы материальных точек с идеальными связями сумма работ всех активных сил и всех сил инерции на любом возможном перемещении в любой фиксированный момент времени равна нулю. Это положение записывается в аналитической форме:

(4.25)

и называется уравнением Даламбера-Лагранжа или общим уравнением динамики. В уравнении (4.25) и – активная сила и сила инерции к-й материальной точки, – ее возможное перемещение, т.е. любое бесконечно малое перемещение, совместимое с наложенными на систему связями в данный фиксированный момент времени (в отличие от действительного малого перемещения, соответствующего бесконечно малому приращению времени t); М – число материальных точек в системе.

Рассмотрим звено механизма, являющееся абсолютно твердым телом. Введем систему координат 0хyz, связанную с этим телом (рис.4.10). Для произвольной точки звена имеем

, (4.26)

где – возможное перемещение полюса 0, – вектор бесконечно малого поворота, – радиус-вектор к-й точки. Подставив (4.26) в (4.25), находим

(4.27)

Здесь и – главные векторы, а и – главные моменты активных сил и сил инерции звенa. Складывая выражения (4.27) для всех подвижных звеньев, приводим уравнение (4.25) для механизма с жесткими звеньями и идеальными кинематическими парами к следующей форме

(4.28)

где N – число подвижных звеньев. Необходимо отметить, что каждое из выражений (4.27) в отдельности нулю не равно, поскольку не равна нулю работа сил реакций, действующих на каждое отдельное звено.

Если механизм имеет w степеней свободы и q₁,…,q_w – его обобщенные координаты, то

(4.29)

Подставляя (4.29) в (4.28) и используя независимость вариаций обобщенных координат q_S, получаем следующую систему уравнений:

. (4.30)

Отметим, что выражение следует понимать не как частную производную от функции положения _i (q₁, …, q_w ), поскольку вектор угла поворота в общем случае вообще не существует как функция положения, а как отношение бесконечно малого угла поворота к бесконечно малому парциальному возможному перемещению q_S. Выражение может рассматриваться также как отношение парциальной угловой скорости к скорости при = 0 для всех ks. Производная является обычной частной производной от функции положения r_0i( q₁, …, q_w) по координате q_S.

Для механизма с одной степенью подвижности система (4.30) сводится к одному уравнению

(4.31)

Поскольку в этом случае , где – скорость точки 0_i, уравнение (4.31) записывается также в форме

(4.32)

Отсюда следует, что сумма возможных мощностей всех активных сил и сил инерции в любой момент времени равна нулю для механизма с одной степенью подвижности при идеальных кинематических парах.

Уравнение Даламбера-Лагранжа в форме (4.28) удобно использовать для определения обобщенных движущих сил. Учитывая, что работа движущей силы Q_S на возможном перемещении q_S равна Q_Sq_S , и выделяя обобщенные движущие силы из прочих активных сил, имеем

(4.33)

где – главный вектор всех активных сил, приложенных к i–му звену, кроме движущих, а – главный момент этих сил. Из (4.33) получаем уравнения, аналогичные (4.30):

. (4.34)

Эти уравнения могут быть непосредственно использованы для определения обобщенных движущих сил Q_S. Отметим, что они остаются в силе и для механизмов с любым числом избыточных идеальных связей. Для механизма с одной степенью подвижности из (4.31) находим:

(4.35)

Рассмотрим в качестве примера задачу об определении движущей силы для рычажного механизма, показанного на рис.4.4. Поскольку в плоском механизме векторы возможных перемещений всех точек параллельны плоскости движения, а векторы малых поворотов звеньев перпендикулярны ей, для составления уравнений Даламбера-Лагранжа достаточно определить компоненты активных сил и сил инерции, лежащие в плоскости движения, и компоненты моментов, ей перпендикулярные. Остальные компоненты сил и моментов не совершают работы на возможном перемещении плоского механизма, а следовательно, и не влияют на величины движущих сил.

Уравнение Даламбера-Лагранжа для механизма, показанного на рис.4.4, составляем в форме (4.35); получаем

(4.36)

где ₂ – абсолютный угол поворота звена 2.

Билет №7. Применение общего уравнения динамики для определения реакции в кинематической паре.

Общее уравнение динамики позволяет определить реакции всех освобождающих связей. Пусть, например, для механизма, показанного на рис.4.4, требуется определить реакцию R₀₃ в поступательной паре. Освободим связь, соответствующую этой реакции; для этого введем условную дополнительную степень подвижности, предположив, что направляющая ползуна может перемещаться в направлении оси y (рис.4.11). Тогда получим механизм с двумя степенями подвижности, в котором координата y_B будет играть роль второй входной координаты, а реакция R₀₃ станет обобщенной «движущей» силой, соответствующей этой координате.

Применим к этому механизму общее уравнение динамики в форме (4.34); для силы R₀₃ получим следующее выражение:

(4.37)

Отметим, что силы и моменты сил инерции, входящие в это выражение, должны определяться при заданных значениях и при y_B = 0, = 0, =0, т.е. они должны вычисляться для заданного движения исследуемого механизма без какого-либо учета дополнительной подвижности. Выражение (4.37) получено из условия равенства нулю работ активных сил и сил инерции на возможном перемещении, соответствующем q = 0, y_B  0. Легко видеть, что при таком перемещении работу будут совершать только силы, приложенные к звеньям 2 и 3. При этом из уравнения (4.37) получим

(4.38)

Из геометрических соображений (см. рис.4.11) можно получить, что

(4.39)

Подставив (4.39) в (4.38), находим величину R₀₃ в заданном положении. Изложенный метод можно применить для определения реакции любой освобождающей связи. Что же касается неосвобождающих связей, то соответствующие им реакции в принципе невозможно определить в процессе силового расчета механизма.

Билет №8. Силовой расчет механизмов, содержащих высшие кинематические пары. Расчет кулачкового механизма методом кинетостатики и с помощью общего уравнения динамики.

Конструктивными элементами, образующими высшую кинематическую пару, являются поверхности, принадлежащие сопрягаемым звеньям. В одних случаях эти поверхности в каждом положении механизма касаются в некоторой точке, в других – касание происходит по некоторой линии. При точечном контакте абсолютно твердых звеньев и при отсутствии сил трения реакции в кинематической паре сводятся к силе R_n, направленной по общей нормали к контактирующим поверхностям. Такая пара является пятиподвижной, и в ней возникает одна неизвестная компонента реакции (рис.4.12, а). При линейном контакте силы взаимодействия (при отсутствии трения) распределены вдоль линии контакта и направлены в каждой точке по общей нормали к поверхностям (рис.4.12, б).

В плоском кулачковом механизме (рис.4.13) линией контакта является прямая, силы взаимодействия лежат в одной плоскости и приводятся к главному вектору , направленному по нормали к поверхности кулачка, и главному моменту , вектор которого лежит в плоскости, касательной к профилю. В этом случае высшая кинематическая пара является четырехподвижной.

Аналогичная картина возникает в прямозубых и косозубых эвольвентных цилиндрических передачах. Здесь, правда, в зацеплении могут одновременно находиться несколько пар зубьев, но все силы контактного взаимодействия лежат в одной плоскости, проходящей через линию зацепления и параллельной осям вращения колес. В конических, червячных и гипоидных передачах линия контакта (если она существует) может оказаться пространственной. При этом и силы взаимодействия образуют пространственную систему: появляются дополнительные компоненты реакций, обычно оказывающиеся «лишними» неизвестными при составлении уравнений силового расчета. В таких случаях идут на упрощение модели кинематической пары, оставляя одну неизвестную компоненту реакции R_n и тем самым переходя к условной схеме точечного взаимодействия. Следует отметить, что при силовом расчете тяжело нагруженных зубчатых передач «жесткая» модель контактного взаимодействия без учета сил трения дает лишь весьма приближенные представления о силовых нагрузках. Чаще всего определение этих нагрузок, связанное с прочностными расчетами, опирается на более сложные модели силового взаимодействия, учитывающие упругую деформацию зубьев, влияние смазки и т.п. Однако рассмотрение таких моделей выходит за рамки этого курса.

Рассмотрим некоторые примеры.

а). Расчет плоского кулачкового механизма. Рассмотрим кулачковый механизм, состоящий из кулачка 1 и поступательно движущегося толкателя 2 (рис.4.14).

Механизм содержит две низших кинематических пары (O и B) и одну высшую (A). В плоскости движения во вращательной паре две неизвестных компоненты реакции – R_01x и R_01y, в поступательной – R₀₂ и , и в высшей кинематической паре – нормальная сила R_12n= – R_21n. Вместе с обобщенной силой Q имеем шесть неизвестных. Для их отыскания можем составить шесть уравнений кинетостатики, которые при равномерном вращении кулачка имеют следующий вид:

R_01x + Ф₁cos t + R_12nsin = 0,

R_01y + Ф₁ sin t – R_12n cos – G₁ = 0,

Q – R_12n ecos – R_12n sin (h₀ + s) –

– G₁ sin t = 0,

R₀₂ – R_12n sin  = 0,

R_12n cos – P – P_пр – Ф₂ – G₂ = 0,

Здесь  t – угол между радиусом 0С₁ (С₁ – центр масс кулачка) и осью x, ₁= 0С₁,  – угол давления, Ф₁ и Ф₂ – силы инерции кулачка и толкателя, G₁ и G₂ – силы тяжести, Р_пр – сила, создаваемая пружиной, прижимающей толкатель к кулачку.

ВОПРОС № 10

Уравнения движения механизма в форме уравнения Лагранжа 2-ого рода. Определение приведенного момента инерции и приведенного момента сил сопротивления (для рычажного и зубчатого механизма)

До сих пор предполагалось, что закон движения механизма является известным: считалось, что он совпадает с программным законом движения, необходимым для выполнения рабочего процесса. В реальной машине закон движения отличается от программного. Это отличие в первую очередь связано со свойствами двигателя, приводящего в движение машину и создающего движущие силы, прикладываемые к входным звеньям. Скорость на выходном звене двигателя зависит от величины обобщенной движущей силы, и это обстоятельство должно учитываться при проектировании машины. В этой связи возникает задача интегрирования системы дифференциальных уравнений движения механической системы совместно с характеристикой двигателя. При этом дифференциальные уравнения движения механизма обычно принимаются в форме уравнений Лагранжа второго рода.

Уравнение Лагранжа второго рода для механической системы (в данном случае – механизма) было получено в курсе теоретической механики:

, (6.1)

где Т(q,) – кинетическая энергия механизма, представленная как функция от обобщенной координаты и обобщенной скорости; Q – обобщенная движущая сила;

(6.2)

– обобщенная сила сопротивления, соответствующая всем активным силам, кроме движущих.

В механизме с одной степенью подвижности кинетическая энергия может быть представлена в форме

(6.3)

Если q – линейная обобщенная координата, то инерционный коэффициент называется приведенной массой механизма; при угловой обобщенной координате имеет размерность момента инерции и называется приведенным моментом инерции. В дальнейшем будет предполагаться, что q – угловая координата, и выражение (6.3) записывается в форме

(6.4)

где J(q) – приведенный момент инерции. Подставляя (6.4) в (6.1) и учитывая, что получаем

(6.5)

П ерейдем к примерам составления уравнений движения механизмов. Рассмотрим кривошипно-ползунный механизм, показанный на рис. 6.1.

Кинетическую энергию механизма определяем как сумму кинетических энергий его подвижных звеньев. Для вращающегося звена 1 имеем

где J₁₀ – момент инерции звена относительно оси вращения. Для поступательно движущегося ползуна 3 получаем Для звена 2, совершающего сложное движение, находим кинетическую энергию, пользуясь теоремой Кёнига, известной из курса теоретической механики: где m₂ – масса звена, – его момент инерции относительно оси, проходящей через центр масс С₂ и перпендикулярной плоскости движения; v_C2 – скорость центра масс; ₂ – угловая скорость. Таким образом, учитывая, что

где  – угол поворота звена 2, получаем

(6.6)

Выражение, стоящее в фигурных скобках, представляет собой приведенный момент инерции механизма J(q). Используя функции положения x_C2(q), y_C2(q), (q), x_B(q), можно было бы представить J(q) в явной форме; однако это аналитическое выражение даже для такого сравнительно простого рычажного механизма оказывается достаточно громоздким. Еще более сложным является выражение . Поэтому на практике часто используются приближенные представления этих функций, основанные на их разложении в ряды Фурье. Легко видеть, что J(q) – периодическая функция с периодом 2; она представима в виде ряда:

(6.7)

Для определения коэффициентов Фурье J₀, J_C1, … , J_S1, … вычисляются значения J(q) при некоторых дискретных значениях q, например, при q = 2k/m (k=1, … m). Для этого используется выражение для J(q) в форме (6.6), а значения производных от функций положения определяются в процессе кинематического анализа механизма. Затем используются известные приближенные соотношения, выражающие коэффициенты Фурье через дискретные значения периодической функции:

(6.8)

Далее составляется приближенное представление функций J(q) и :

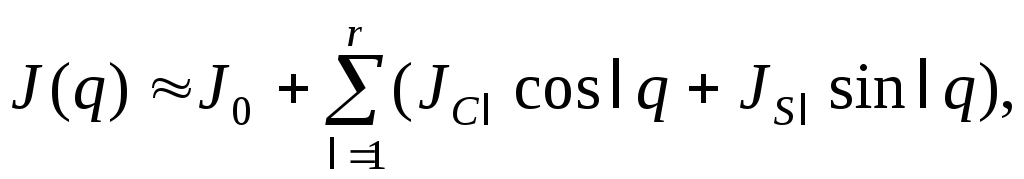(6.9)

(6.10)

Удовлетворительная аппроксимация для – й гармоники получается только при условии m  4. Следует также иметь в виду, что пренебрежение высшими гармониками в выражении для приведенного момента инерции ограничивает область применимости уравнения (6.5).

Для составления уравнения Лагранжа необходимо также определить обобщенную силу Q_С как функцию от Предположим, что силами тяжести звеньев механизма можно пренебречь, и единственной активной силой сопротивления является сила P (см. рис.6.1), возникающая при выполнении рабочего процесса и зависящая от и Тогда по формуле (6.2) находим

(6.11)

Обобщенная сила Q_С часто называется приведенным моментом сил сопротивления. Функция Q_С(q,) является также периодической по q с периодом 2. Если входное звено связано с кривошипом передаточным механизмом с передаточным отношением i, то период равен 2i.

В качестве второго примера рассмотрим механизм с линейной функцией положения, показанный на рис. 6.2. Он состоит из двухступенчатой передачи (колеса 1 – 4) и ротора 5. Пусть J₁, J₂, J₃, J₄, J₅ – моменты инерции вращающихся масс относительно их осей вращения; z₁, z₂, z₃, z₄ – числа зубьев колес; M_С – момент сил сопротивления, приложенных к ротору. Составляя выражение для кинетической энергии системы, имеем

(6.12)

В этом случае приведенный момент инерции не зависит от координаты q. Обобщенная сила Q_С определяется в соответствии с (6.2):

(6.13)

Подставляя (6.12) и (6.13) в (6.5), получаем уравнение движения

(6.14)

где

(6.15)

– приведенный момент инерции механизма. Отметим, что при приведении вращающихся масс момент инерции каждой из них делится на квадрат передаточного отношения, связывающего эту массу с входным звеном.

Уравнение Лагранжа второго рода может быть использовано, так же как и уравнение Даламбера-Лагранжа, для определения обобщенной движущей силы Q. При заданном законе движения входного звена из уравнения (6.5) находим:

(6.16)

Однако роль уравнений Лагранжа в динамике машин этим не исчерпывается. Как уже отмечалось, они используются так же, как дифференциальные уравнения движения механической системы машины, из которых определяется закон движения q(t). В обоих случаях для составления уравнений Лагранжа необходимо знать зависимости Определение этих функций в аналитической форме требует обычно достаточно громоздких преобразований, связанных с составлением выражения для кинетической энергии и его дифференцированием, а также с определением работы активных сил. В связи с этим для решения первой задачи (определения обобщенной движущей силы по заданному закону движения) чаще всего используются уравнения кинетостатики или уравнения Даламбера-Лагранжа. Более того, легко показать, что эти же уравнения позволяют определить для заданного значения q величины а при заданных q и – величину Q_С.

Действительно, пусть мы определили с помощью, например, уравнений кинетостатики величину обобщенной движущей силы Q при следующих условиях: т.е. при нулевом значении угловой скорости входного звена, единичном угловом ускорении и при отсутствии активных сил (что эквивалентно Q_С = 0). Предположим, что при этих условиях (Hм). Подставив выбранные значения в уравнение (6.16), находим, что

т.е. что величина Q_1 численно совпадает с величиной J(q_), выраженной в Нмс². Таким образом, для определения J(q_) нет необходимости составлять выражение для кинетической энергии механизма, его можно определить с помощью уравнений кинетостатики, если их применить для некоторого «условного» закона движения. Задавая различные значения q_ и повторяя эту процедуру, найдем значения J(q) в ряде дискретных точек, что позволяет аппроксимировать эту функцию, например, отрезком ряда Фурье (6.9). Найдем теперь (Нм) при q=q_, и при отсутствии сил сопротивления. Подставив эти значения в (6.16), получим Наконец, задав найдем при заданных силах сопротивления; тогда из (6.16) получим

ВОПРОС № 11

Уравнения Лагранжа 2-ого рода для механизма с несколькими степенями подвижности.

Уравнения Лагранжа второго рода для механизма с w степенями подвижности, с жесткими звеньями и идеальными кинематическими парами могут быть получены из общего уравнения динамики, записанного в форме (4.28). Работа сил инерции на возможном перемещении, входящая в это уравнение, может быть выражена через кинетическую энергию системы. Для механизма с w степенями подвижности справедливо:

= (6.17)

где Т(q₁, …, q_w,) – кинетическая энергия механизма с w степенями подвижности, представленная как функция от обобщенных координат и их производных. В результате при независимых обобщенных координатах уравнения (4.34) приводятся к виду:

(s = 1, … , w) , (6.18)

где Q_s – обобщенные движущие силы;

(6.19)

– обобщенные силы сопротивления, соответствующие всем активным силам, кроме движущих.

Кинетическая энергия каждого звена в общем случае определяется как кинетическая энергия твердого тела, совершающего сложное пространственное движение:

, (6.20)

где i – номер звена, m_i – его масса, v_ci – скорость центра масс, J_сi – тензор инерции в системе осей, начало которой находится в центре масс i-го звена, – трехмерный вектор-столбец абсолютной угловой скорости. Учитывая, что

, (6.21)

где J_ix, J_iy, J_iz – осевые моменты инерции i-го звена, J_ixy, J_ixz, J_iyz – центробежные моменты инерции, а

, (6.22)

где – проекции вектора угловой скорости i-го звена на оси i-й системы координат, выражение (6.20) запишем в виде:

(6.23)

В качестве примера рассмотрим схему трехподвижного механизма (рис. 6.3). Звено 1 вращается вокруг своей продольной оси с угловой скоростью . По звену 1 со скоростью движется звено 2. Звено 3, связанное со звеном 2 шарниром В, вращается относительно звена 2 с угловой скоростью . На звене 3 имеется схват, в точке М которого приложена активная сила . Центры масс второго и третьего звеньев находятся в точках С₂ и С₃ соответственно.

Кинетическую энергию механизма определим как сумму кинетических энергий его подвижных звеньев. Для вращающегося звена 1 имеем где – момент инерции звена 1 относительно оси z₁, совпадающей с осью его вращения.

Звено 2 вращается вместе со звеном 1 и перемещается по нему, его кинетическая энергия равна:

,

где v_с2 – скорость центра масс второго звена, m₂ – его масса, J₂ – тензор инерции, построенный в осях С₂x₂y₂z₂ (рис. 6.4, а), – вектор-столбец угловой скорости звена 2, составленный из проекций угловой скорости на оси той же системы координат С₂x₂y₂z₂.

Найдем v_с2 и :

,

.

Подставим найденные значения в выражение для кинетической энергии Т₂:

,

где . Кинетическая энергия третьего звена Т₃:

.

Найдем скорость центра масс третьего звена v_с3.

,

,

Положим, что звено 3 представляет собой тонкий однородный стержень, а . Тогда компоненты тензора инерции J₃, построенного в осях С₃x₃y₃z₃ (рис. 6.4, б): J_3x = 0; J_3y = J_3z = ; J_3xy = J_3xz = J_3yz = 0. Угловая скорость :

.

Отсюда получим:

.

Полная кинетическая энергия механизма составит:

Найдем обобщенные силы сопротивления. Из выражения (6.19) следует:

.

Здесь учтено, что центр масс звена 1 не изменяет своего положения. Из кинематического анализа несложно получить выражения для и : , , , , , .

Функция положения точки М:

.

Отсюда

, , ,

; ; ,

, , .

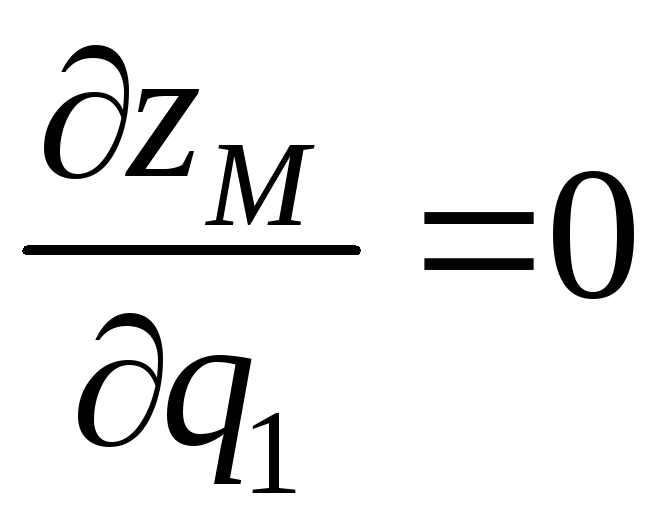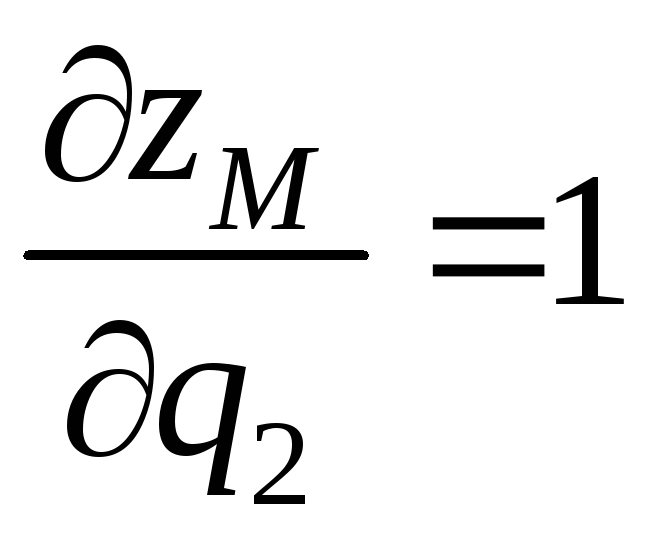Теперь несложно найти обобщенные силы сопротивления:

,

,

.

Подставляя найденные значения в уравнения Лагранжа, получим три уравнения движения:

Из приведенных уравнений видно взаимовлияние приводов. Например, двигатель 2 «чувствует», как работает двигатель, приводящий в движение звено 3 (движущий момент Q₂ зависит от и от ).

ВОПРОС № 12

Трение в кинематических парах. Трение скольжения, качения и верчения. Модель высшей КП с точечным контактом.