Монотонность функции на промежутках. Исследование функций на монотонность

1. Монотонность функции.

Функцию   называют возрастающей  на множестве  (где - область определения функции  ), если для любых точек   и   таких, что   выполняется неравенство  . Если это неравенство является строгим  , то функцию   называют строго возрастающей на множестве  .

Таким образом, функция   называется:

a)     возрастающей на множестве  , если

  :       ;

строго возрастающей на множестве  , если

  :       ;

б) убывающей на множестве  , если

  :       ;

 строго убывающей на множестве  , если

  :       ;

Убывающие и возрастающие функции объединяют названием монотонные, а строго возрастающие и строго убывающие - названием строго монотонные.

 

Будем говорить, что функция   строго возрастает в точке  , если существует   такое, что

,

.

Аналогично  строго убывает в точке  , если существует   такое, что

,

.

 

Экстремумы функции.

 Пусть существует  число   такое, что функция   определена в   - окрестности точки  , т.е. на множестве  , и пусть для всех   выполняется неравенство

.

Тогда говорят, что функция   имеет в точке   локальный минимум.

Аналогично, если существует число   такое, что для всех   выполняется неравенство

,

то говорят, что функция   имеет в точке   локальный максимум.

Локальный min и max объединяются общим термином локальный экстремум.

 

 

 

 

 

 

 

 

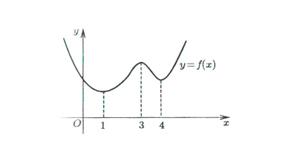
На рисунке функция    имеет локальные экстремумы, а именно минимумы при   и   и максимум при  .

Выпуклость функций

а) График функции   называется выпуклым в интервале  , если он расположен ниже касательной, проведенной в любой точке этого интервала.

 

 

График функции   называется вогнутым в интервале  , если он расположен выше касательной, проведенной в любой точке этого интервала.

б) Непрерывная функция   называется выпуклой на отрезке  , если для любых точек   и  отрезка   выполняется неравенство

 

.

 

Аналогично, функция   называется вогнутой на отрезке  , если для любых точек   и  отрезка   выполняется неравенство

 

.

Асимптоты графика функции. Необходимое и достаточное условие существования наклонных асимптот.

Если расстояние от точки M кривой y = f(x) от некоторой прямой y = kx + b стремиться к нулю, когда точка M, двигаясь по кривой, удаляется в бесконечность, то прямая y = kx + b называется асимптотой кривой y = f(x).    Асимптоты могут быть вертикальными, наклонными и горизонтальными.    Пусть кривая y = f(x) имеет одну или несколько вертикальных асимптот    Для нахождения вертикальных асимптот кривой y = f(x) нужно отыскать такие значения x = a, при которых yобращается в бесконечность, т.е. при которых  .    Уравнение вертикальной асимптоты будет

x = a     

   В самом деле, из рис.1 непосредственно видно, что расстояние точки M(x; y) от прямой x = a равно d = | x - a |. Когдаx  a, то точка M(x; y) движется по кривой y = f(x), удаляясь в бесконечность, причем ее расстояние d = | x - a | от прямой x = a стремится к нулю и, согласно определению асимптоты, прямая x = a является асимптотой кривой y = f(x)

Однако не всегда легко представить уравнение кривой в виде (3). Поэтому для нахождения наклонной асимптоты сначала определяют угловой коэффициент k, а потом отрезок b, отсекаемый асимптотой на оси Oy. Выведем формулы для вычисления k и b.     Запишем условие (3) в виде

   При x  + слагаемое   стремится к нулю, а потому

     (4)

   Теперь из уравнения

f(x) = kx + b + 

находим b:

b = f(x) - kx - 

или, так как  ,

     (5)

   Если пределы (4) и (5) существуют, то кривая имеет при x+ асимптоту

y = kx + b,

где k и b находятся по формулам (4) и (5). Для x- формулы такие же, но пределы находятся при x-.    При k = 0 получаем уравнение

y = b

горизонтальной асимптоты, причем