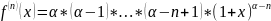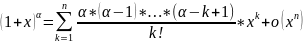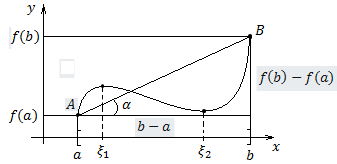
Теорема Лагранжа
Пусть
непрерывна
на
,
дифференцируема на
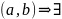по
меньшей мере одна точка
,
такая, что выполняется
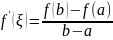
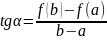
Доказательство
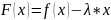– вспомогательная
функция,
– параметр подобранный специальным
образом.
(непрерывна
на
и
дифференцируема
)
подберём таким образом, чтобы
удовлетворялись условия теоремы Ролля
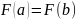
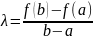
По теореме Ролля
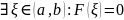
Замечание
Из теоремы Лагранжа вытекает формула конечных приращений Лагранжа
Применив
теорему Лагранжа для
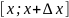
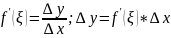– конечное
приращение Лагранжа.
Конечному приращению аргумента соответствует конечное приращение функции.
Теорема Коши
Пусть
и
непрерывны
на
и
дифференцируемы на
,
причём
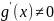на
по меньшей мере одна точка
,
такая, что выполняется равенство
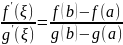
Доказательство
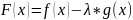
Эта функция непрерывна на и дифференцируема на подберём таким образом, чтобы для удовлетворялась теорема Ролля; т.е.
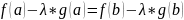
По теореме Ролля
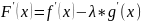
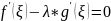
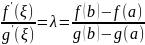
Раскрытие
неопределенности
.
Правило Лопиталя.
Пусть
и
определены
в некоторой окрестности точки
,
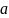за исключением точки
возможно
и пусть выполняются следующие условия:
и непрерывны в этой окрестности, за исключением точки возможно
и
дифференцируемы
в этой окрестности, за исключением
точки
возможно,
причём
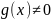
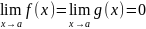
(конечный
или бесконечный)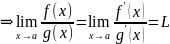
правило Лопиталя
Доказательство
Доопределим
и
в
точке
по
непрерывности, т. е. положим
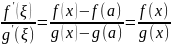По
теореме Коши
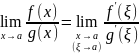
Замечания:
Условия теоремы могут быть сформулированы относительно полуокрестностей(правого или левого предела) правило Лопиталя для одностороннего предела
Правило
применяется, когда
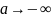или
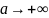
Правило
Лопиталя можно применять неоднократно,
если применение правила даёт нам ту же
неопределенность
и
в отношени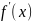и
и
имеет
место условие теоремы
Раскрытие неопределённости . Правило Лопиталя.
Пусть и определены в некоторой окрестности точки , за исключением точки возможно и пусть выполняются следующие условия:
и непрерывны в этой окрестности, за исключением точки возможно
и дифференцируемы в этой окрестности, за исключением точки возможно, причём
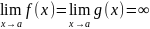
(конечный
или бесконечный)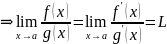
правило Лопиталя
Доказательство
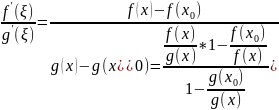
0
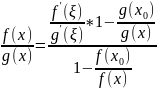
0
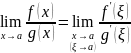
Замечания:
Условия сформулированные в теореме могут относится к правой или левой окрестности(полу-) точки , в этом случае в правиле речь идёт об односторонних пределах
Правило
Лопиталя имеет место когда,
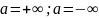
Правило
Лопиталя может применяться многократно,
если
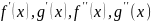удовлетворяют
условию теоремы
Раскрытие
неопределённости вида
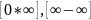
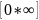
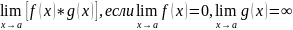
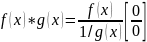
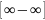
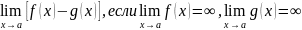
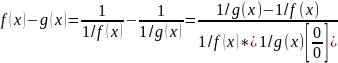
Раскрытие
неопределённости вида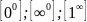
.
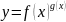
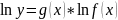
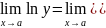
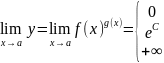
Формула Тейлора
Пусть
определена
и
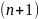раз
дифференцируема в некоторой окрестности
точки
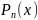«близко»
к
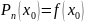
и
так далее
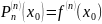
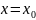
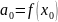
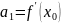
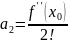
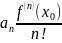
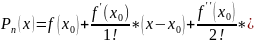
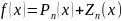Формула
Тейлора
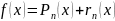
– остаточный член;
может быть записан в виде: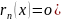
– форма Пеано
Для остаточного члена:
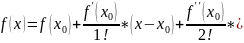– остаточный член
в форме Лагранжа
Разложение
функции
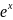по формуле Тейлора.
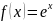
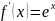
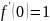
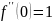
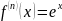
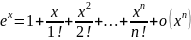
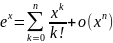
Разложение
функции
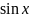по формуле Тейлора.
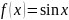
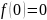
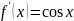
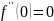
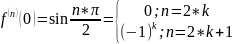
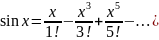
Разложение
функции
по формуле Тейлора.
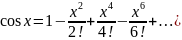
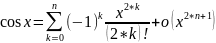
Разложение
функции
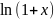по формуле Тейлора.
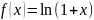
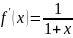
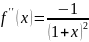
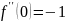
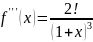
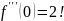
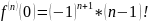
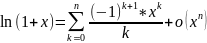
Разложение
функции
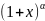по формуле Тейлора.
