§2. Модель оценивания финансовых активов (сарм).

Данная модель базируется на теории формирования портфеля активов. В ее основу положен ряд допущений:

1. Все инвесторы имеют дело с одним и тем же совершенным рынком.

2. Все инвесторы имеют один и тот же инвестиционный горизонт, т.е. они планируют инвестиции на один и тот же период.

3. Все инвесторы ведут себя рационально, т.е. все они выбирают оптимальные (в смысле теории Марковица) портфели, исходя из индивидуальных предпочтений, которые описываются функцией полезности (определяемой индивидуальным коэффициентом неприятия риска).

4. Все инвесторы одинаково оценивают рынок. Формально это означает, что все инвесторы исходят из одних и тех же значений параметров рынка: вектора ожидаемых доходностей и матрицы ковариаций.

5. На рынке имеется безрисковый портфель с фиксированной доходностью.

6. Позиции игроков на рынке никак не ограничиваются. Они могут занимать длинные и короткие позиции любой величины по любым активам. Причем, активы бесконечно делимы, так что веса портфелей могут принимать любые вещественные значения.

Основной моделью рынка является модель Блека- Тобина-Шарпа-Линтнера с безрисковым активом, которую можно называть стандартной.

В стандартной модели предполагается наличие безрискового актива А₀ с доходностью r_б, которая не зависит от состояния рынка и всегда имеет одно и то же значение. Остальные активы А₁, …, А_n – рисковые, т.е. имеют ненулевую дисперсию.

Линия рынка капитала (CML) отражает зависимость между риском и доходностью эффективных портфелей, т.е. для портфелей, сочетающих рисковые и безрисковые активы.

Эффективные портфели. Портфель, для которого на заданном множестве портфелей не найдется портфеля, имеющего оценку с большей доходностью или меньшим риском, называется эффективным портфелем на этом множестве.

Если на координатной плоскости (σ,R) изобразить кривую, представляющую зависимость «риск – доходность» для портфеля, состоящего только из рисковых активов, и провести к ней касательную из точки (0, r_б), обозначающей безрисковый актив, то можно отметить следующее.

Данная прямая, представляющая собой эффективно множество стандартной модели, касается верхней ветви гиперболы - эффективной границы рисковых активов, в точке, соответствующей оценке касательного портфеля.

Поскольку в САРМ принята гипотеза однородных ожиданий (условие 4), то из совпадения оценок параметров рынка для всех инвесторов следует, что критериальные множества, их границы и касательные портфели также будут совпадать для всех инвесторов. Поскольку, в силу условия рациональности (условие 3), каждый инвестор выбирает оптимальные по Марковицу портфели, то эти портфели будут эффективными. Их оценки для всех инвесторов будут лежать на одной и той же эффективной границе – рассмотренной выше касательной. Причем, на этой же линии лежат оценки двух фиксированных портфелей: безрискового и касательного.

Из этих фактов следует основной вывод САРМ (теорема о разделении или теорема о двух фондах): оптимальный портфель любого инвестора является линейной комбинацией всего двух фиксированных портфелей – безрискового и касательного (рискового).

Эффективная граница модели Тобина называется линией рынка капитала (capital market line - CML). Поскольку данная линия – прямая, проходящая через оценки безрискового и касательного портфеля, то ее уравнение имеет вид:

1. R = r_б + σ(r_t – r_б )/σ_t,

где r_t – доходность, а σ_t – риск касательного портфеля.

Рыночный портфель. Если рассмотреть структуру касательного портфеля, то можно отметить следующее. Пусть на рынке обращаются активы - А₁, …, А_n и, вместе с тем, имеется m участников В₁, …, В_m – инвесторов, которые покупают и продают эти активы. Пусть каждый инвестор располагает начальным капиталом К_i ,i = 1, …, m. При этом каждый из участников формирует оптимальный, с учетом своего отношения к риску, портфель – (х₀, х₁, … , х_n)ⁱ. Здесь х₀ – доля начального капитала, инвестируемая в безрисковый актив, а х₁, … , х_n – рисковая часть портфеля инвестора.

Начальный инвестируемый капитал К_i инвестора В_i распределится таким образом на две части: рисковую – W_i = (1 – х₀ⁱ ) К_i и безрисковую – U_i = х₀ⁱ К_i , так что К_i = W_i + U_i . Следовательно, совокупный рисковый капитал, вложенный во все рисковые активы, составляет:

(2.2) W = W₁ + … + W_m.

Поскольку все инвесторы вкладывают рисковую часть в один и тот же касательный портфель τ = (τ₁, …, τ_n), то очевидно, k – й инвестор вложит в j – й рисковый актив τ_j – ю долю своего рискового капитала W_j, т.е. w_j^k = τ_j W_k. Таким образом, общая сумма средств, вложенных в j - й рисковый актив, составляет:

(2.3) w_j =w_j¹ + w_j² + … + w_j^m = τ_j W₁ + … + τ_j W_m = τ_j (W₁ + … + W_m)= τ_j W.

Отсюда следует, что

(2.4) τ_j = w_j /W,

то есть вес j – го актива в этом портфеле равен рыночной доле этого актива, т.е. отношению суммы средств, вложенных в этот актив, к общей сумме средств, вложенных во все рисковые активы.

Таким образом, в условиях рыночного равновесия цены на рисковые активы устанавливаются в соответствии с формулой (2.4). Именно в силу данного обстоятельства касательный портфель называют также рыночным портфелем. Тогда, если σ_М – его СКО, а r_М – ожидаемая доходность, то уравнение (2.1) можно переписать в виде

(2.5) R = r_б + σ(r_М – r_б )/σ_М.

Поскольку оценки всех эффективных портфелей лежат на эффективной линии рынка (CML), то для любого такого портфеля π_э будет выполнено соотношение

(2.6) R(π_э)= r_б + σ(π_э)(r_М – r_б )/σ_М.

Бета и характеристическая линия рынка. Уравнение эффективной линии рынка устанавливает линейную связь между доходностью и риском эффективных портфелей.

В рамках модели САРМ установлена также более глубокая линейная связь между доходностью и риском любых портфелей и, в частности, любых активов. Однако мерой риска в этой связи выступает не традиционно принимаемая характеристика – СКО доходности, а величина, называемая бетой портфеля (актива).

Определение: бетой случайной величины R относительно случайной величины S называется число:

(2.7) β_R =

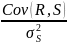
Бета доходности R_π портфеля π или доходности R_А актива А относительно доходности R_М рыночного портфеля π_М называется бетой портфеля (актива) и обозначается β_π (соответственно, β_А):

(2.8) β_π = _.

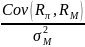Учитывая, что в соответствии с (1.13)

(2.9) cov(R_π, R_М) = ρ_πМ σ_π σ_М,

формулу (2.8) можно представить в виде

(2.10) β_π = ρ_πМ σ_π /σ_М,

где ρ_πМ - коэффициент корреляции портфеля с рынком.

Приведенную выше характеристику называют теоретической бетой, в отличие эмпирической или статистической беты.

Из свойств ковариации следует, что бета портфеля π с весами – (х₁, … , х_n) является линейной комбинацией бет, составляющих портфель:

(2.11) β_π = β₁х₁ + … + β_n х_n

Можно отметить, что бета эффективного портфеля равна весу рискового портфеля

(2.12) β_π = х_М

Используя предыдущие соображения, бету и формулу (2.5), можно получить уравнение эффективной линии рынка.

Допустим, что существует некоторый рыночный портфель активов, доходность которого равна r_m , а волатильность – σ_m. На рынке также можно разместить активы по безрисковой процентной ставке r_f. Пусть на рынке обращается некоторый актив k с доходностью r_k и риском σ_k. Рассмотрим новый портфель, в состав которого с весами, соответственно, х_k и х_m включены рассмотренные выше актив и рыночный портфель. Его характеристики будут следующими:

ожидаемая доходность

(2.13) r_p = x_m r_m + x_k r_k

дисперсия

(2.14) σ²_p = x²_m σ²_m + x²_k σ²_k + 2 x_k x_m σ_mk,

где σ_mk – ковариация актива k с рыночным портфелем.

Поскольку

(2.15) x_m + x_k = 1,

то, обозначив x_m = х, х_k = 1 – x , r_p = r, σ_p = σ можно получить следующие соотношения

(2.16) r = x r_m + (1 – x) r_k

(2.17) σ² = x² σ²_m + (1 – x)² σ²_k + 2 x(1 – x) σ_mk

Рис.1

Предполагая, что рассматриваемый актив относится к допустимому множеству, его соотношение с рыночным портфелем также задает некоторое допустимое множество портфелей, которое определяется соотношениями (2.16)-(2.17). При этом очевидно, с уменьшением значения (1 – х) – доли актива k в рассматриваемом портфеле, происходит трансформация нового портфеля в рыночный. А поскольку зависимость r = r(σ), заданная соотношениями (2.16)-(2.17) является непрерывной и дифференцируемой функцией, то в точке x = 1 производная этой функции совпадает с производной функции, задающей рыночный портфель. Следует заметить, что на плоскости (r,σ) точка с координатами (r_m, σ_m ), во – первых, задает рыночный портфель, а, во – вторых, согласно модели САРМ, принадлежит линии рынка капитала, причем эта линия является касательной к графику, определяющему эффективные рыночные портфели (Рис. 1). Наклон линии рынка капитала определяется из ее уравнения (2.18) путем вычисления производной (dr/dσ)

(2.18) r = r_f + (r_m – r_f) σ / σ_m.

Очевидно,

(2.19) (dr/dσ) = (r_m – r_f) / σ_m.

Теперь необходимо найти производную функции r = r(σ), заданной параметрически соотношениями (2.16)-(2.17). Производная таких функций определяется по формуле

(2.20) (dr/dσ) =(dr/dх)/(dσ/dх)

Вычисление производных (dr/dх) и (dσ/dх) дает следующие соотношения:

(2.21) (dr/dх) = ( x r_m + (1 – x) r_k ) ^‘ = r_m – r_k

(2.22) (dσ/dх) = ( )'

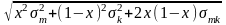(2.23) (dσ/dх) = ( x σ²_m – (1 – x) σ²_k +(1 – 2 x) σ_mk )/ σ,

где, согласно (2.17)

σ(х) =

В точке x = 1 с учетом того, что σ(1) = σ_m , получаем

(2.24) (dσ/dх) = (σ²_m – σ_mk ) / σ_m

Следовательно,

(2.25) (dr/dσ) =(dr/dх)/(dσ/dх) = σ_m (r_m – r_k )/ (σ²_m – σ_mk)

Теперь, приравнивая (2.19) и (2.25), получаем соотношение

(2.26) (r_m – r_f) / σ_m = σ_m (r_m – r_k )/ (σ²_m – σ_mk),

откуда следует, что

(2.27) r_k = r_f + (r_m – r_f ) σ_mk /σ²_m,

Теперь, если учесть формулу (2.8), которая определяет величину β_k , то искомое уравнение примет вид

(2.28) r_k = r_f + β_k(r_m – r_f ).

Имея соотношение (2.28) для отдельного актива, можно получить и соотношение линии рынка для любого портфеля π, которое примет следующий вид, учитывая формулу (2.11)

(2.29) r_π= r_f + β_π(r_m – r_f )

Оказывается, что это соотношение выполняется не только для эффективных, но и для всех портфелей вообще, и, в частности, для всех активов. Это утверждение составляет содержание второго важнейшего результата САРМ.

Уравнение характеристической линии рынка. Для любого портфеля или актива справедливо соотношение:

(2.30) R_π = r_f + β_π(r_m – r_f )

Уравнение (2.30) называется характеристическим уравнением рынка или основным уравнением САРМ. Оно описывает линейную связь между ожидаемой доходностью портфеля и его бетой, представляющей еще одну характеристику риска.

Уравнение (2.30) может быть переписано в виде:

(2.31) R_π – r_f = β_π(r_m – r_f )

Отсюда следует, что бета портфеля играет роль «коэффициента усиления», преобразующего рыночную премию (r_m – r_f ) в премию по портфелю R_π – r_f. Другими словами, бета является мерой чувствительности доходности портфеля к изменениям рыночной доходности. Действительно, из (2.31) следует

32. ΔR_π = β_π Δr_m.

Таким образом, прирост ожидаемой доходности активов с β_π > 1 будет больше, чем прирост рыночной премии, а у активов с β_π < 1, соответственно, меньше.

Уравнение (2.30) указывает, что на равновесном совершенном рынке инвестору компенсируется не полный риск портфеля, характеризуемый СКО σ, а только его часть, представляющая рыночный (систематический, недиверсифицируемый) риск, характеризуемый параметром бета.

В явном виде разложение доходности и риска на систематическую и несистематическую компоненты задается в однофакторной модели Шарпа.

Однофакторная модель рынка. Однофакторная модель Шарпа описывает влияние на доходность акций важнейшего фактора - поведение рынка в целом. Основное уравнение этой модели дает разложение доходности актива на компоненты:

(2.33) R_i = α_i + β_i r_М + ε_i

где R_i - доходность актива А_i ;

α_i – фиксированный параметр, представляющий нерыночную составляющую доходности актива А_i ;

β_i - параметр_, отражающий влияние изменения рыночной доходности на доходность i – го актива при изменениях доходности рыночного портфеля;

r_М – доходность рыночного портфеля;

ε_i – случайная ошибка, причем Е(ε_i) = 0 и D(ε_i) = δ_i ².

При этом предполагается, что выполнены условия независимости:

(2.34) cov (ε_i , ε_j ) = 0, cov(ε_i , r_М ) = 0 для любых i и j.

Уравнение (2.33) называется характеристическим уравнением актива. Слагаемое α_i + ε_i называется специфической, а β_i r_М - неспецифической частью доходности актива А_i. Аналогично на две части разлагается и риск актива. Недиверсифицируемый, систематический или рыночный риск связан с общим состоянием рынка общезначимыми для всех активов событиями. Его нельзя исключить полностью, поэтому его называют также неустранимым риском. Нерыночный, диверсифиуируемый, специфический или устранимый риск связан с индивидуальными особенностями конкретного актива и его эмитента. Данный риск является диверсифицируемым, т.к. его можно свести практически к нулю с помощью эффективной диверсификации портфеля. Вычислим дисперсию ожидаемой доходности R_i..

Можно показать, основываясь на соотношениях (2.33) и (2.34), что диверсификация инвестиций в рыночные активы приводит минимизации риска, в частности, к уменьшению его специфической части и выделению его систематической составляющей.

Как известно, для ожидаемой доходности и дисперсии портфеля имеем

35. Е = ∑х_i Е_i , σ² = ∑∑ х_i х_j c_ij, а c_ij = cov(R_i, R_j)

Тогда из (2.33) и (2.34) следует

(2.36) c_ii = D(R_i), c_ii = β_i²σ_М² + δ_i ² , c_ij = β_i β_j σ_М², i ≠ j

(2.37) σ² = ∑∑ х_i х_j c_ij = ∑∑ х_i х_j β_i β_j σ_М² + ∑ х_i ² δ_i ²

Поскольку выполнено (2.36), то получаем

(2.38) σ² = (∑х_i β_i)(∑ х_j β_j )σ_М² + ∑ х_i ² δ_i ²

Теперь, если определить коэффициент бета для портфеля

(2.39) β = ∑х_i β_{i ,}

то из (2.38) следует

(2.40) σ² = β²σ_М² +∑ х_i ² δ_i ²

Полученное соотношение содержит два слагаемых, первое из которых характеризуется рыночными параметрами, а второе – присущими только самим активам. Можно рассмотреть случай, когда доли активов в портфеле одинаковы

(2.41) x₁ = x₂ = … = x_n = 1/n, тогда

(2.42) ∑ х_i ² δ_i ² = (1/n)² ∑δ_i ² ≤ (1/n)² n δ_max ² = δ_max ²/n.

Очевидно, сумма в левой части (2.42) стремится к нулю при больших значениях n, тогда в данных условиях риск хорошо диверсифицированного портфеля определяется систематическим риском входящих в портфель активов и может быть представлен в виде

(2.43) σ² = β²σ_М².

Таким образом, диверсификация инвестиций в рыночные активы приводит к уменьшению риска, присущего самим активам, сам же совокупный риск портфеля при этом ограничивается систематической его частью.

Рассматривая отдельный актив в рамках однофакторной модели, можно обнаружить следующее. Что касается дисперсии ожидаемой доходности R_i , то, очевидно из (2.33) и (2.35) следует

(2.44) D(R_i) = D(α_i + β_i r_М + ε_i) = D(α_i )+ D(β_i r_М )+ D(ε_i) = β_i ²D( r_М) + δ_i ².

Или

(2.45) σ_i² = β_i ²σ_М² + δ_i ².

Следовательно, полный риск актива также представлен рыночной составляющей β_i ²σ_М² и величиной, характеризующей собственно саму сущность актива – δ_i ². Очевидно, что коэффициент бета β_i служит мерой систематического, рыночного риска, где, по определению

(2.46) β_i = cov(R_i, r_М)/σ_М² = ρ_iМ σ_i /σ_М.

cov(R_i, r_М) – ковариация доходности R_i актива А_i с доходностью рыночного портфеля.

Характерно, что формулы (2.45) – (2.46) справедливы не только для отдельных активов, но и для любых портфелей, в частности, для портфеля π

(2.47) σ_π² = β_π ²σ_М² + δ_π ².

На практике беты активов находят, используя в качестве представителя рыночного портфеля некоторый индекс. В этом случае бета актива определяется по формуле (2.46), где в качестве cov(R_i, r_М) и σ_М используются полученные по выборке статистические оценки этих величин.