Построение эвольвентных профилей зубьев нулевого и корригиро- ванного зубчатых колес методом огибания (обкатки)
Цель работы:
1) Ознакомление с теоретическими основами процесса нарезания стандартных (нулевых) и корригированных цилиндрических зубчатых колес с эвольвентным профилем зуба по методу огибания;
2) Получение практических навыков расчета геометрических параметров нулевых зубчатых колес и колес, нарезанных со смещением инструмента.
Ход работы :
Лабораторная установка и исходные данные для вычислений:
Таблица 6.1
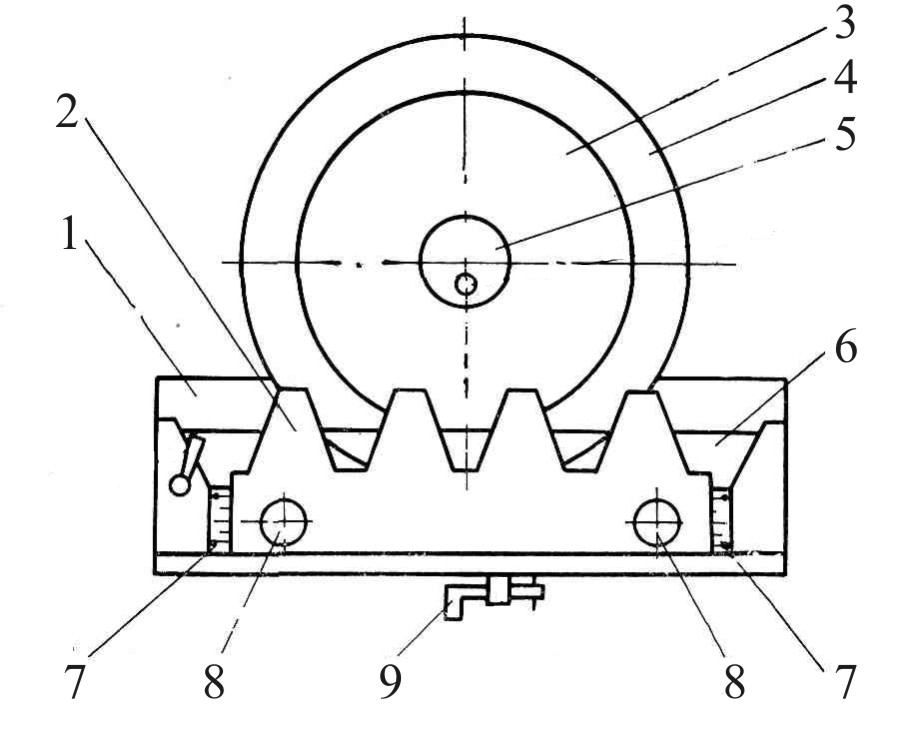
Схема установки
Рис.1 |
Заданные величины:
1. Модуль рейки .
. . . . . . . . . .
2. Угол профиля рейки . . . . . . ____ град; 3. Коэффициент высоты
головки зуба . . .
. . . . . . . . . . .
4. Коэффициент радиального
зазора . . . . . . . . .
. . . . . . . . . . .
5. Диаметр делительной
окружности . . . . .
. . . . . . . .
|
____
мм;
1,0
;
0,25;
____
мм;
Параметры нулевого колеса 1 при Таблица 6.2
№ п/п |
Определяемые величины |
Расчетные формулы, вычисления, результаты измерений |
1 |
Число зубьев колеса |
|
2 |
Угол зацепления колес 1 и 2 |
при
|
3 |
Радиус делительной окружности |
|
4 |
Радиус основной окружности |
|
5 |
Радиус окружности впадин |
|
6 |
Радиус окружности вершин |
|
7 |
Радиус начальной окружности |
при
|
8 |
Шаг зубьев по делительной окружности: - расчетный . . . . . . . . . . .
- измеренный . . . . . . . . . . |
|
9 |
Шаг зубьев по основной окружности: - расчетный . . . . . . . . . . .
- измеренный . . . . . . . . . . |
|
10 |
Толщина зуба по делительной окружности: - расчетная . . . . . . . . . . .
- измеренная . . . . . . . . . . |
|
11 |
Толщина зуба по основной окружности: - расчетная . . . . . . . . . . .
- измеренная . . . . . . . . . . |
|
12 |
Толщина зуба по окружности вершин зубьев: - расчетная . . . . . . . . . . .
- измеренная . . . . . . . . . . |
|
13 |
Толщина зуба по начальной окружности: - расчетная . . . . . . . . . . .
- измеренная . . . . . . . . . . |
|
____
;
20°
;
_____
мм;
_____
мм;
__
мм;
___
мм;
_____
мм;
_____
мм;
_____
мм;
_____
мм;
_____
мм;
_____
мм;
_____
мм;
____ мм;
____ мм;
=__мм;
____
мм;
_____
мм;
_____
мм;
Параметры корригированного колеса 1
при
___
и
Таблица
6.3
№ п/п |
Определяемые величины |
Расчетные формулы, вычисления, результаты измерений |
1 |
Относительный сдвиг рейки |
|
2 |
Абсолютный сдвиг рейки |
|
3 |
Угол зацепления колес 1 и 2 |
=____;
|
4 |
Коэффициент воспринимаемого смещения |
|
5 |
Коэффициент уравнительного смещения |
|
6 |
Радиус делительной окружности |
|
7 |
Радиус основной окружности |
|
8 |
Радиус окружности впадин |
|
9 |
Радиус окружности вершин |
|
10 |
Радиус начальной окружности |
|
11 |
Шаг зубьев по делительной окружности: - расчетный . . . . . . . . . . .
- измеренный . . . . . . . . . . |
|
12 |
Шаг зубьев по основной окружности: - расчетный . . . . . . . . . . .
- измеренный . . . . . . . . . . |
|
13 |
Толщина зуба по делительной окружности: - расчетная . . . . . . . . . . .
- измеренная . . . . . . . . . . |
|
14 |
Толщина зуба по основной окружности: - расчетная . . . . . . . . . . .
- измеренная . . . . . . . . . . |
|
15 |
Толщина зуба по окружности вершин зубьев: - расчетная . . . . . . . . . . .
- измеренная . . . . . . . . . . |
|
16 |
Толщина зуба по начальной окружности: - расчетная . . . . . . . . . . .
- измеренная . . . . . . . . . . |
|
____
;
____;
________=____
мм;
_____;
=_______=____;
=
________ =_____;
_____
мм;
_____
мм;
=
_____ мм;
=
_____ мм;
____
мм;
_____
мм;
_____
мм;
____
мм;
_____
мм;
= _____ мм;
_____
мм;
=
____ мм;
____ мм;
=___
____
мм;
=__;
_____
мм;
Выводы: _____________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
Работу выполнил: _____________ Работу принял: _______________
1 Леонард Эйлер (1707-1783) – знаменитый математик и механик, член Петербургской академии наук с 1727 г., предложил решение задачи о профилировании зубьев в плоских зубчатых передачах с использованием эвольвентных профилей.
2 Другими словами, при вращении звеньев точка не должна перемещаться по линии центров.
3 Исходный контур, являющийся основой для получения эвольвенты, имеет также более общее название - эволюта. В общем случае, в качестве эволюты может быть использована любая кривая.
4
На
чертежах показывают упрощенное
изображение переходной кривой в виде
сопряженной с другими контурами колеса
дуги радиусом
,
где
-
модуль зуба. Допускаются и другие формы
переходной кривой, учитывая, что эта
часть колеса не участвует в зацеплении.
5 Такой же модуль должен иметь зуборезный инструмент для нарезания данного зубчатого колеса.
6 Отсюда название метода – «метод огибания» или «метод обката».
7 Отсюда название «нулевое» зубчатое колесо.
8 От лат. corrigo — исправляю, улучшаю.