Рисунки до задач д. 11. 0. – д. 11. 3.

Рисунки до задач д. 11. 4. – д. 11. 6.

Рисунки до задач д .11. 7. – д. 11. 9.

де Т – кінетична енергія системи; – узагальнена сила, що відповідає координаті q₁; Q₂ – узагальнена сила, що відповідає координаті q₂.

В загальному випадку кінетична енергія системи дорівнює сумі кінетичних енергій всіх тіл, що входять в систему:

Для тіл, які відсутні в системі (прочерк у відповідному стовпчику) і тіл, маса яких дорівнює нулю (нуль у відповідному стовпчику), кінетична енергія дорівнює нулю.

Розв’язання задачі Д.11 необхідно починати з вибору узагальнених координат:

де x – подовження пружини, яке вимірюється в бік того з тіл 3, 4 або 5, до якого прикріплена пружина. Наприклад, якщо пружина прикріплена в точці А, то її довжина в довільній момент часу дорівнює АВ і

де – довжина недеформованої пружини;

φ – кут повороту крайнього блока, який при цьому може бути і невагомим. Кут φ необхідно відраховувати від початкового положення блока. Якщо блоки 1 і 2 в систему не входять, а входять лише тіла 3 і 4, необхідно покласти

,

де y – відстань тіла 4 від початкового положення. Відповідні приклади дані на рис. Д.11.10 а, б, в.

Хід розв’язання подано в прикладах, що наведені нижче. У всіх прикладах необхідно врахувати, що тіло 3 здійснює складний рух i

де . Переносну швидкість необхідно знайти відповідно до рисунка задачі.

За правильне розв’язання задачі Д.11 з використанням даних таблиці Д.11.0–Д.11.9 студент одержує оцінку „задовільно”. За правильне розв’язання задачі Д.11 з використанням даних таблиці Д.11.0.А–Д.11.9.А студент одержує оцінку „добре”, а з використанням даних таблиці Д.11.0.Б–Д.11.9.Б – оцінку „відмінно”.

Приклад розв’язання задачі Д.11. Перший рівень складності.

Механічна система (рис. 21.32 ) складається з блоків 1 і 2, вага яких відповідно дорівнює Р₁=4Р і Р₂=0, візка 4 ваги Р₄=5Р та пружини АВ, жорсткість якої дорівнює с. Радіуси ступінчастих блоків 1 і 2 дорівнюють відповідно: R₁=R, r₁=0,4R, R₂=R, r₂=0,8R. При обчисленні моментів інерції всі блоки вважати однорідними суцільними циліндрами радіуса R. На систему, крім сил ваги, діє пара сил з моментом М₁=4РR, яка прикладена до блока 1.

Рис. 21. 32.

Дано: Р₁=4Р ; Р₂=0; Р₃= - ; Р₄=5Р ; Р₅= - ; F=0; M₁=4PR; M₂=0; пружина АВ; с.

Визначити: 1) , де x – подовження пружини; 2) частоту k і період τ коливань.

Розв’язання. Система, що вивчається в цій задачі, має два ступені вільності. За узагальнені координати вибираємо кут повороту φ блока 1 і подовження пружини x. Запишемо рівняння Лагранжа другого роду у вигляді

(1)

(2)

Визначимо кінетичну енергію Т системи, яка дорівнює сумі кінетичних енергій всіх тіл

(3)

(Т₂=0, Т₃=0, Т₅=0 – див. “Методичні вказівки”).

Блок 1 обертається навколо осі О₁, його кінетична енергія дорівнює

. (4)

Момент інерції дорівнює

.

Тоді

. (5)

Візок здійснює складний рух, тому

Враховуючи протилежні напрями швидкостей, маємо

. (6)

Кінетична енергія візка 4 дорівнює

(7)

Отже, повна кінетична енергія системи дорівнює

(8)

З рівності (8) знаходимо похідні:

(9)

(10)

(11)

Обчислюємо узагальнені сили. Нехай x=const (пружина не розтягується), тоді елементарна робота

(12)

Нехай φ=const (блоки не обертаються), тоді елементарна робота, враховуючи силу пружності пружини F_пр=cx:

(13)

З рівнянь (9), (10), (11), (12) і (13) складаємо рівняння Лагранжа другого роду:

(14)

(15)

Розв’язуємо систему двох рівнянь з двома невідомими:

З останніх рівнянь знаходимо

(16)

Позначимо

(17)

тоді

(18)

Рівняння (18) – звичайне неоднорідне лінійне диференціальне рівняння з постійними коефіцієнтами. Загальне розв’язання однорідного диференціального рівняння

запишемо у формі

(19)

Частинний розв’язок неоднорідного диференціального рівняння шукаємо у вигляді

(20)

Знайдемо похідні:

З рівняння (18) знаходимо

звідси

(21)

Загальний розв’язок неоднорідного диференціального рівняння

(22)

Знайдемо закон зміни швидкості:

(23)

З початкових умов і рівнянь (22) і (23) знаходимо

(24)

(25)

Отже

(26)

При відомій циклічній частоті k період коливань дорівнює

(27)

Відповідь: колова частота коливань

період коливань

рівняння руху візка

Примітка. Якщо до візка 4 прикладена сила , то елементарна робота цієї сили дорівнює:

Узагальнена сила Q₂ (див. формулу (13)) буде визначатись так:

Приклад розв’язання задачі Д.11. Другий рівень складності.

Механічна система (рис. 21.33) складається з ступінчастих блоків 1 і 2, радіуси яких дорівнюють відповідно R₁=R, r₁=0,8R, R₂=R, r₂=0,4R, котка 3 (блоки і коток - однорідні циліндри) і візка 4 ваги Р₄=2Р. Вагою коліс візка нехтуємо. До котка прикладена сила . Між візком і блоком 2 (ділянка АВ) поміщена пружина, жорсткість якої дорівнює с. До блока 1 прикладена пара сил з моментом M₁=4PR. Система починає рух зі стану спокою; пружина в цей момент не деформована.

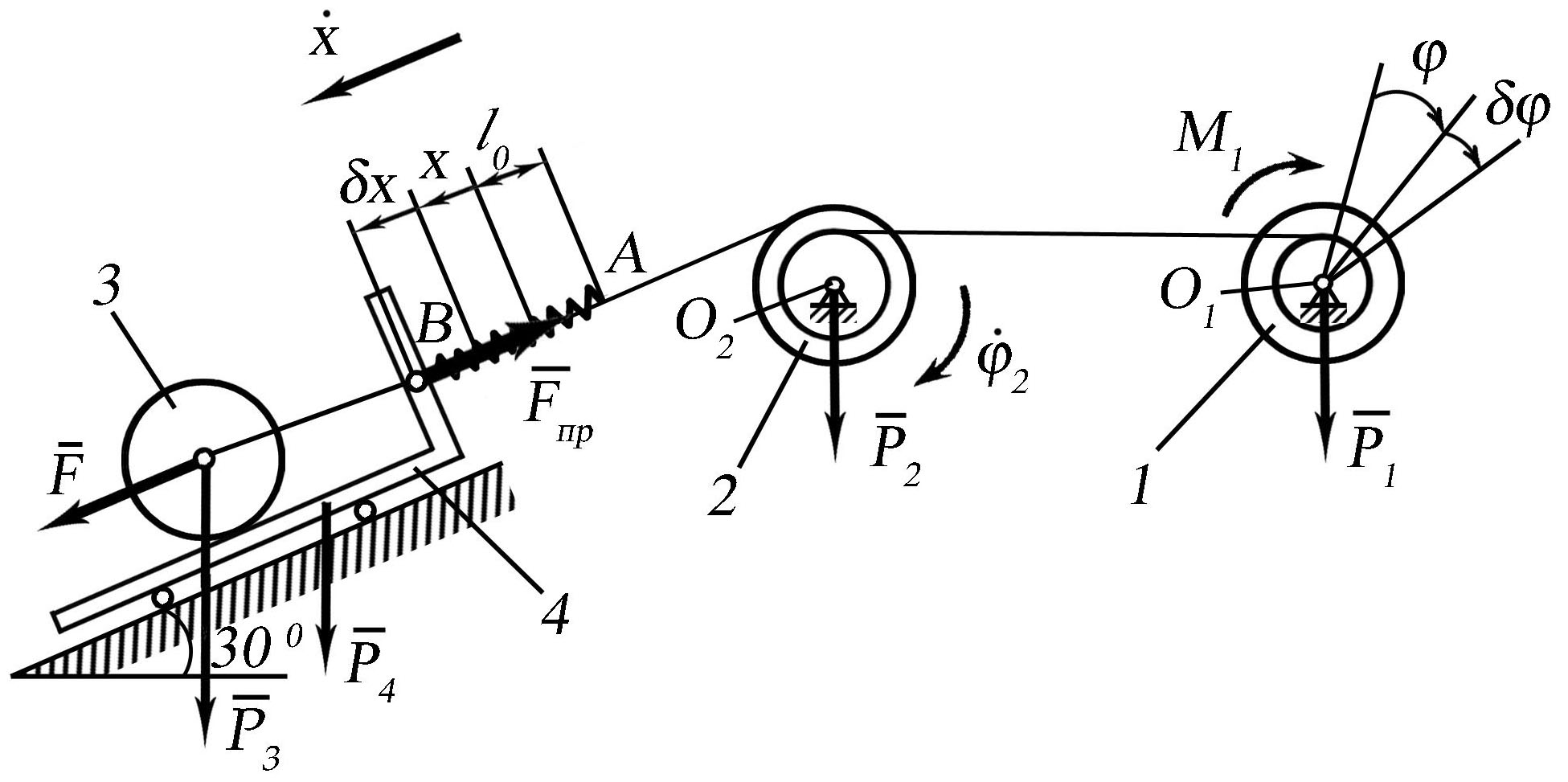
Рис. 21. 33.

Дано: R₁=R; r₁=0,8R; R₂=R; r₂=0,4R; Р₁=4Р; Р₂=2Р; Р₃=0,7Р; Р₄=2,5Р; F=0; M₁=4PR; пружина АВ; с.

Визначити: 1) , де x – подовження пружини (переміщення візка); 2) частоту k і період τ коливань.

Розв’язання. Система, що вивчається в цій задачі, має два ступені вільності. За узагальнені координати приймаємо кут повороту φ блока 1 і подовження x пружини. Запишемо рівняння Лагранжа другого роду у вигляді

(1)

(2)

Обчислимо кінетичну енергію Т системи, яка дорівнює сумі кінетичних енергій тіл даної системи

. (3)

Блок 1 здійснює обертальний рух навколо осі О₁. Його кінетична енергія Т₁ дорівнює

.

Момент інерції блока 1

,

а тому

. (4)

Блок 2 здійснює обертальний рух навколо осі О₂. Його кінетична енергія Т₂ дорівнює

З рис. 21.33 маємо

; .

Тому

. (5)

Тіла 3 і 4 здійснюють складний рух (тіло 3 відносно тіла 4 не рухається). А тому

.

Враховуючи напрям швидкостей, маємо

. (6)

Кінетична енергія візка і котка дорівнює

(7)

Повна кінетична енергія системи дорівнює

(8)

Від рівності (8) знаходимо похідні:

(9)

(10)

(11)

Знаходимо узагальнені сили. Нехай x=const, тоді елементарна робота активних сил

Отже

Q₁=0,8PR. (12)

Нехай =const, тоді елементарна робота активних сил

Отже

Q₂=1,6P cx. (13)

З рівнянь (10) і (13), (11) і (12) складаємо рівняння Лагранжа другого роду і розв’язуємо систему двох рівнянь:

(14)

(15)

;

;

(16)

Позначимо

(17)

Період коливань дорівнює

(18)

Рівняння (16) перепишемо так:

. (19)

Однорідне рівняння має загальний розв’язок

. (20)

Частинний розв’язок запишемо у формі

(21)

Звідси знайдемо

; . (22)

Підставимо вирази (21) і (22) в рівняння (19), одержимо

звідси

(23)

Загальний розв’язок неоднорідного диференціального рівняння має вигляд

(24)

звідси знайдемо похідну за часом:

. (25)

Початкові умови мають вигляд

і рівняння (24) і (25) дають такі сталі інтегрування:

; ;

; ; .

Отже, рівняння (24) перепишемо так:

. (26)

Відповідь: рівняння руху

;

колова частота коливань

;

період коливань

.

Примітка. Якщо до котка 3 (або візка 4) буде прикладена сила (n – деяке число), то елементарна робота цієї сили буде дорівнювати:

.

Це призведе до збільшення узагальненої сили Q₂ (див. рівняння (13)):

.

Приклад розв’язання задачі Д.11. Третій рівень складності.

Механічна система (рис. 21.34) складається з ступінчастих блоків 1 і 2, котка 3, візка 4 і тягаря 5.

Рис. 21.34.

Сили ваги цих тіл дорівнюють відповідно Візок з’єднано з блоком 2 намотаною на нього ниткою. Коток з’єднано з візком 4 пружиною BD,коефіцієнт жорсткості якої . На коток діє сила , а на блок 1 – момент М₁ і момент сил опору М_о. Система починає рухатись зі стану спокою; пружина в цей момент не деформована.

Дано: R₁=R₂=R; r₁=0,4R; r₂=0,2R; Р₁=1,5Р; Р₂=2Р; P₃=0,5Р; Р₄=0,1Р; Р₅=4Р; F=Р; М₁=2РR; М₂=0,1РR; пружина BD; с.

Визначити: 1) , де x – подовження пружини (або переміщення центра D котка відносно візка); 2) частоту k і період τ коливань.

Розв’язання. Дана система має два ступені вільності. За узагальнені координати приймаємо кут повороту φ блока 1 і подовження пружини x (q₁=; q₂=x). Запишемо рівняння Лагранжа другого роду у вигляді

(1)

(2)

Обчислимо кінетичну енергію Т системи, яка дорівнює сумі кінетичних енергій тіл даної системи

. (3)

Тіло 1 здійснює обертальний рух. Його кінетична енергія дорівнює

Тіло 2 також здійснює обертальний рух. Його кінетична енергія

З рисунка 21.34 знаходимо

; ,

отже

Тіло 4 здійснює поступальний рух. Його кінетична енергія дорівнює

Тіло 5 також здійснює поступальний рух. Його кінетична енергія дорівнює

Тіло 3 здійснює складний рух. Його швидкість дорівнює

; ;

Враховуючи напрям швидкостей, маємо

.

Кутова швидкість тіла 3:

.

Кінетична енергія тіла 3 дорівнює

де

.

Повна кінетична енергія системи дорівнює

(4)

Від виразу (4) знаходимо похідні:

(5)

(6)

;

(7)

Обчислимо узагальнені сили. При x=const елементарна робота активних сил

Отже

. (8)

При =const елементарна робота активних сил

Отже

. (9)

З рівнянь (5), (6) і (8); (5), (7) і (9) складаємо рівняння Лагранжа другого роду і розв’язуємо систему:

; (10)

; (11)

;

. (12)

Останнє рівняння перепишемо так:

(13)

Позначимо

; (14)

. (15)

Рівняння (13) перепишемо так:

. (16)

Однорідне диференціальне рівняння

має загальний розв’язок

. (17)

Частинний розв’язок неоднорідного диференціального рівняння запишемо у формі

(18)

звідси знайдемо похідні:

; . (19)

Підставимо рівності (18) і (19) в (16), одержимо

,

звідси

(20)

Загальний розв’язок неоднорідного диференціального рівняння має вигляд

; (21)

звідси знайдемо похідну за часом

(22)

Початкові умови мають вигляд

, ,

і рівності (21) і (22) дають такі сталі інтегрування:

; ;

; ; .

Отже, рівність (21) перепишеться так:

. (23)

Відповідь: рівняння коливань

;

циклічна частота коливань

;

період коливань

.

415