Четырехвектор импульса.

Напомним, что 4^х-вектором называется совокупность 4-х величин , , , , преобразующихся при переходе от одной ИСО к другой по закону:

; ; ; , (36)

где ; , т.е. подчиняются преобразованиям Лоренца.

Компоненту 4^х-вектора называют временной, а компоненты пространственными. Если пространственные компоненты образуют трехмерный вектор в координатах то нет необходимости различать контра- и ковариантные компоненты. Компоненты вектора обычно записывают с индексами снизу.

Квадрат 4^х-вектора, определяемого выражением (36) – 4^х-скаляр – инвариантная величина:

. (37)

Рассмотрим частицу, движущуюся со скоростью в системе отсчета . Пусть

–

перемещение частицы за время . Из этих величин можно образовать 4^х-вектор пространства – времени:

, (38)

где трехмерный вектор, аналогичный 4^х-вектору, введенному в главе “Интервал”.

Домножим компоненты 4^х-вектора (38) на постоянную величину (что, естественно, оставляет его 4^х-вектором), где масса покоя, а собственное время частицы.

// // = = = // // =

4^x-вектор,

а его длина

^_ = = inv . (39)

Используя выражение (21), связывающее полную энергию с релятивистской массой частицы, можем записать

, или - (40)

это импульс-энергия - четырехмерный вектор с инвариантной длиной

, (41)

или

. (42)

Т.о., в релятивистской механике импульс и энергия являются компонентами одного четырехвектора, из чего непосредственно вытекают формулы преобразования энергии и импульса при переходе из одной системы отсчета в другую:

; ; ; . (43)

Выполнение законов сохранения импульса и энергии является экспериментальным фактом. При описании некоторого процесса с помощью 4^х-вектора импульса-энергии можно сказать, что если пространственные компоненты 4^х-вектора импульса-энергии сохраняются ( ), то его временная компонента тоже сохраняется ( ).

Пример: Две частицы движутся в направлении оси с импульсами и и неупруго сталкиваются. Рассмотрим их неупругое столкновение в системах и :

4^х-вектор импульса-энергии в системе до столкновения:

4^х-вектор импульса-энергии в системе до столкновения:

компонента 4^х-вектора при переходе из системы в систему преобразуется в компоненту следующим образом:

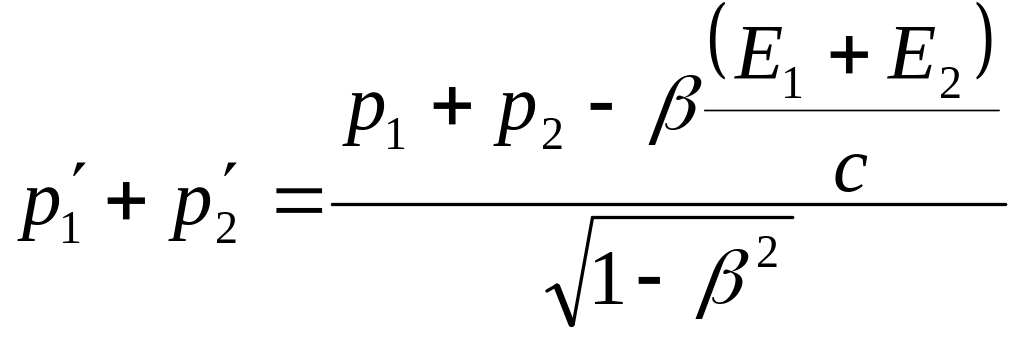(44)

Пусть в результате неупругого столкновения импульс составной частицы равен в системе и в системе , а 4^х-векторы частицы, соответственно, равны:

и .

Найдем связь между нулевыми компонентами 4^х-вектора импульса-энергии до и после столкновения.

Связь между импульсами в штрихованной и нештрихованной системах отсчета:

(45)

Из закона сохранения импульса имеем

Тогда из равенств (44) и (45) получаем закон сохранения нулевой компоненты, т.е. энергии:

(46)

Из рассмотренного примера следует интересный факт, что при неупругом соударении энергия сохраняется! Таким образом, полная релятивистская энергия включает в себя и внутреннюю энергию частиц.

Как результат:

1. каждой частице можно сопоставить релятивистскую энергию ; (47)

2. если система состоит из нескольких частиц, то их полная релятивистская энергия системы равна сумме энергий отдельных частиц

3. при взаимодействии энергия отдельной частицы может изменяться, но их полная (суммарная) энергия системы частиц сохраняется.

8.2. Одна частица.

1. Полная энергия свободной частицы: (48)

2. Если частица покоится (её скорость в рассматриваемой системе отсчета), то она обладает энергией покоя

(49)

Энергия покоя - это та постоянная, с точностью до которой определяется энергия частиц.

3. Инвариант энергии-импульса для одной частицы

(50)

Если рассматриваем задачу в системе, где частица покоится и ее импульс , то , и

получаем

(51)

4. Кинетическая энергия частицы определяется как разность её полной энергии и энергии покоя

, (52)

. (53)

Связь между импульсом и кинетической энергией частицы следует из (53)

. (54)

5. Переход к законам классической механики ( или ) осуществляется путем разложения функции в ряд при малых значениях аргумента :

Пренебрегая высшими степенями малых параметров, получаем

. (55)

6. Полезная формула, связывающая энергию и импульс частицы, получается из уравнений

.

Разделив второе уравнение на первое, имеем:

(56)

7) В ядерной физике и физике высоких энергий принято характеризовать частицы не их скоростями, а энергиями.

Частицу называют нерелятивистской, если её кинетическая энергия много меньше энергии покоя ( ). В этом случае импульс частицы определяется как .

Релятивистской называют частицу, для которой выполняется соотношение . Импульс релятивистских частиц с массой покоя, отличной от нуля, приближенно описывается той же формулой, что и для безмассовых частиц, т.е. .

В ультрарелятивистском пределе (когда скорости частицы близка к скорости света и ):

(57)