
16.3. Теорема Штейнера.
Теорема: Момент инерции тела относительно произвольной оси равен сумме момента инерции
![]() относительно
оси
относительно
оси
![]() ,
параллельной данной и проходящей через
центр инерции тела, и
,
параллельной данной и проходящей через
центр инерции тела, и
произведения массы тела на квадрат расстояния между осями.
![]()
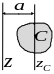 (16.10)
(16.10)
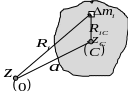
Доказательство теоремы.
Пусть точка
![]() центр
инерции тела. Проведем через произвольный
элемент
центр
инерции тела. Проведем через произвольный
элемент
![]() плоскость, перпендикулярную осям
и
,
проходящим через центр инерции тела
плоскость, перпендикулярную осям
и
,
проходящим через центр инерции тела
![]() и точку
.
Векторы
и точку
.
Векторы
![]() и
и
![]() задают, соответственно,
положение элемента
относительно осей
и
,
а вектор
задают, соответственно,
положение элемента
относительно осей
и
,
а вектор
![]() – взаимное расположение этих осей.
– взаимное расположение этих осей.
При этом
![]() .
(16.11)
.
(16.11)
Тогда момент инерции относительно оси равен
![]() .
.
В этом выражении последнее слагаемое дает момент инерции
относительно оси , проходящей через центр инерции тела.
Второе слагаемое равно нулю.
Действительно,
![]() вектор-проекция
радиус-вектора
вектор-проекция
радиус-вектора
![]() ,
,
определяющего
положение элемента
![]() относительно центра
относительно центра
инерции тела, на рассматриваемую плоскость. Относительно
центра инерции
вектор
![]() (что следует из определения центра
инерции), следовательно, и сумма
векторов-проекций также равна нулю:
(что следует из определения центра
инерции), следовательно, и сумма
векторов-проекций также равна нулю:
![]() .
.
В первом слагаемом
![]() .
.
Итак, теорема Штейнера (16.10) доказана.
Пример. Используя теорему Штейнера, найдем момент инерции диска относительно оси , проходящей через
его край перпендикулярно плоскости диска:
![]() .
.
16.4. Главные моменты инерции.
Вообще говоря, моменты инерции, определенные относительно различных осей, проходящих через центр инерции тела, различны.

В общей теории доказывают, что для тела любой формы и с произвольным распределением массы существуют три взаимно перпендикулярные, проходящие через центр инерции тела оси, которые могут служить свободными осями.
Такие оси называются главными осями инерции тела, а моменты инерции относительно их называются главными моментами инерции.
Важной особенностью
главных осей инерции является то, что
при вращении тела вокруг любой из них
направление вектора момента импульса
![]() совпадает с направлением вектора угловой
скорости тела
и
совпадает с направлением вектора угловой
скорости тела
и
![]() .
.
Для тел с
центральной симметрией (шаровые
волчки) равны
все главные моменты инерции:
![]() .
Пример:
шар, куб.
.
Пример:
шар, куб.
Для тел с осевой
симметрией (симметрические
волчки) равны
два из трех главных моментов инерции:
![]() .
Пример:
цилиндр
.
Пример:
цилиндр
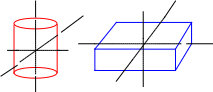
![]() .
.
Пример: параллелепипед.
Вращение вокруг осей, соответствующим максимальным и минимальным значениям моментов инерции, является устойчивым, а вокруг других – неустойчивым. Примеры:
Вращение коробка спичек. При внешнем воздействии наиболее устойчиво то вращение, которое соответствует максимальному значению главного момента инерции.
Вращение диска, закрепленного за край с помощью нити.
Обратим внимание, что главные оси инерции не обязательно проходят через центр инерции тела.
Для несимметричного (или неоднородного) тела момент импульса , вообще говоря, не совпадает по направлению с вектором угловой скорости . Из рисунка легко понять, что момент импульса выделенной
пунктиром симметричной части тела совпадает по направлению с вектором угловой скорости.
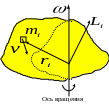 Однако момент
импульса каждой части тела
Однако момент
импульса каждой части тела
![]() ,
не входящей в
,
не входящей в
мысленно выделенную
симметричную, дает дополнительный вклад
![]()
в момент импульса всего тела. Из-за этой “добавки” получаем, что
вектор момента импульса несимметричного (неоднородного) тела,
вращающегося как показано на рисунке, отклоняется от направления
вектора угловой скорости.
При вращении несимметричного (неоднородного) тела момент
импульса описывает конус, ось которого направлена по вектору
угловой скорости и
![]() .
.
Но всегда верно
соотношение, связывающее проекцию
момента импульса на ось вращения, с
угловой скоростью
![]() :
:
![]() .
.
Если момент
инерции тела во время движения не
изменяется (![]() ),
то:
),
то:
![]() ,
или
,
или
![]() ,
(16.12)
,
(16.12)
где
![]() суммарный
момент всех внешних сил относительно
оси вращения, а
суммарный
момент всех внешних сил относительно
оси вращения, а
![]()
проекция вектора
углового ускорения
![]() на ось вращения.
на ось вращения.
Итак, при вращении вокруг свободных (главных) осей связь между моментом импульса вращающегося тела и его угловой скоростью наиболее проста:
![]()
или, если координатные
оси (![]() )
совпадают с главными осями вращения:
)
совпадают с главными осями вращения:
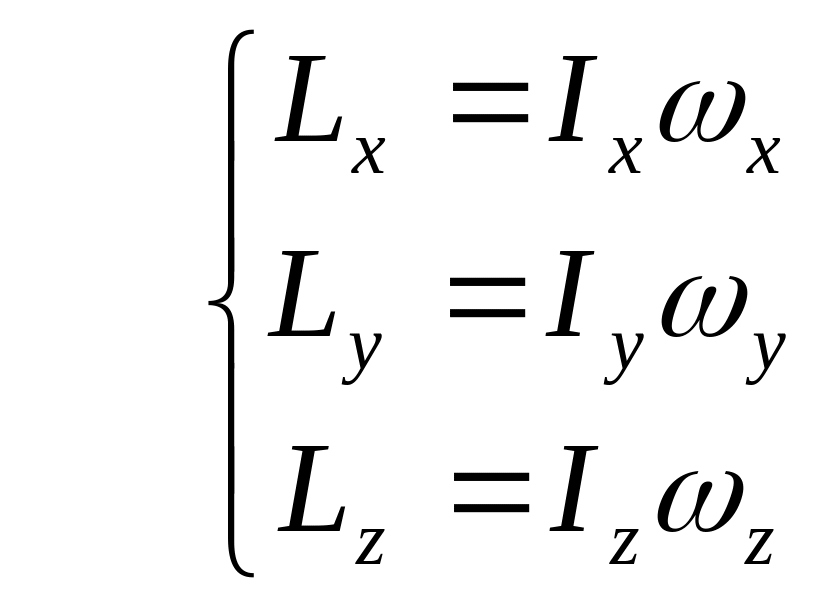 .
(16.13)
.
(16.13)
Однако если ось вращения не является свободной (главной) и произвольно ориентирована относительно координатных осей ( ), то связь между компонентами момента импульса и угловой скорости становится более сложной:
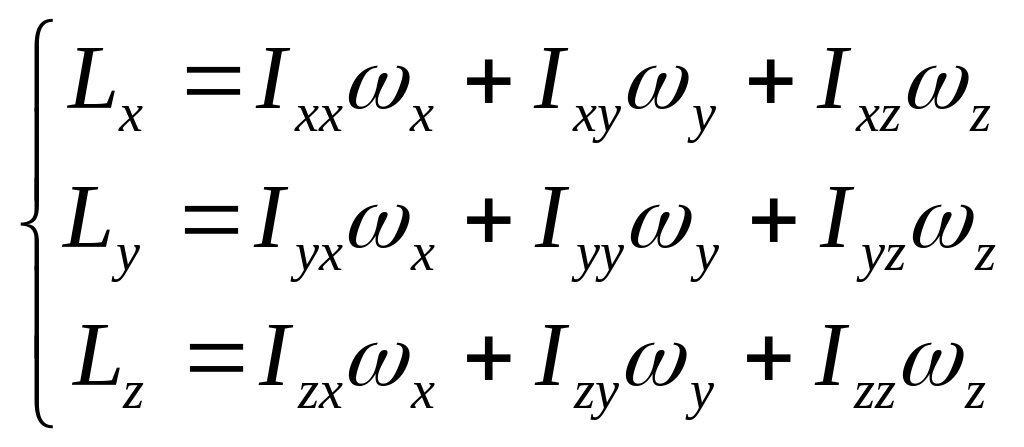 .
(16.14)
.
(16.14)
Здесь
![]() - коэффициенты пропорциональности,
имеющие размерность момента инерции.
- коэффициенты пропорциональности,
имеющие размерность момента инерции.
Частные случаи:
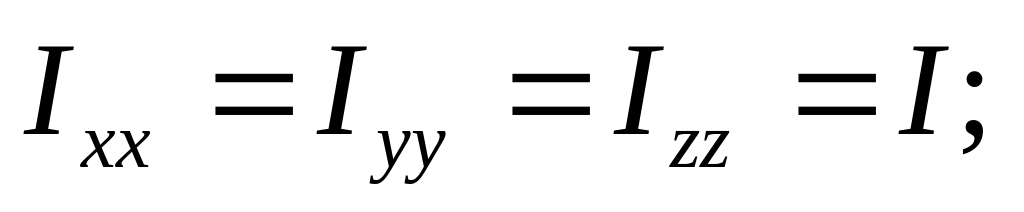 т.е.
т.е.
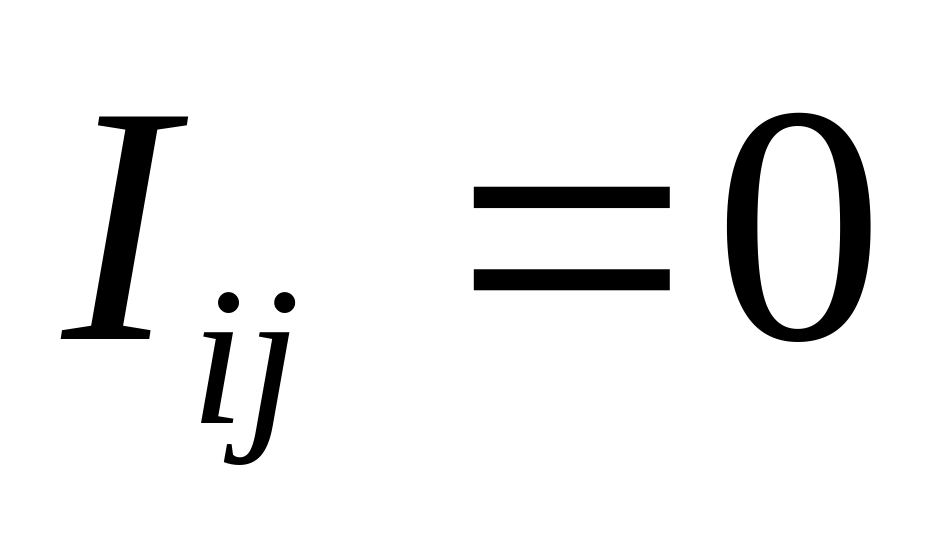 для
для
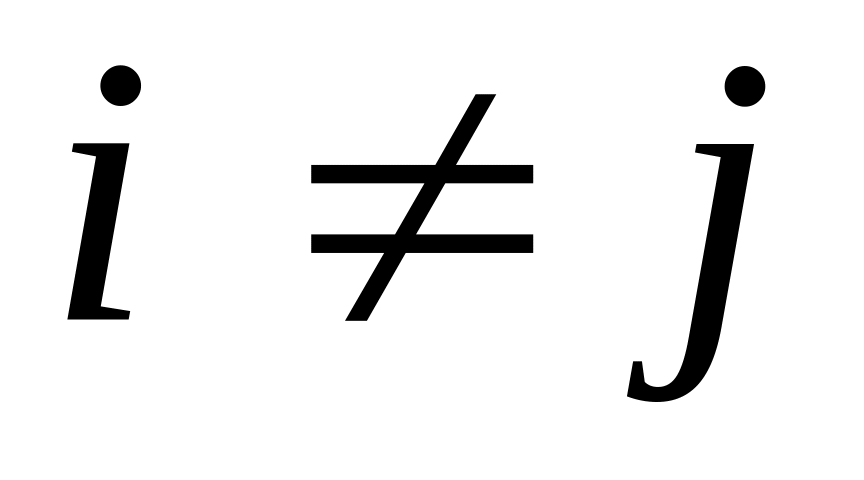 ,
то
,
то
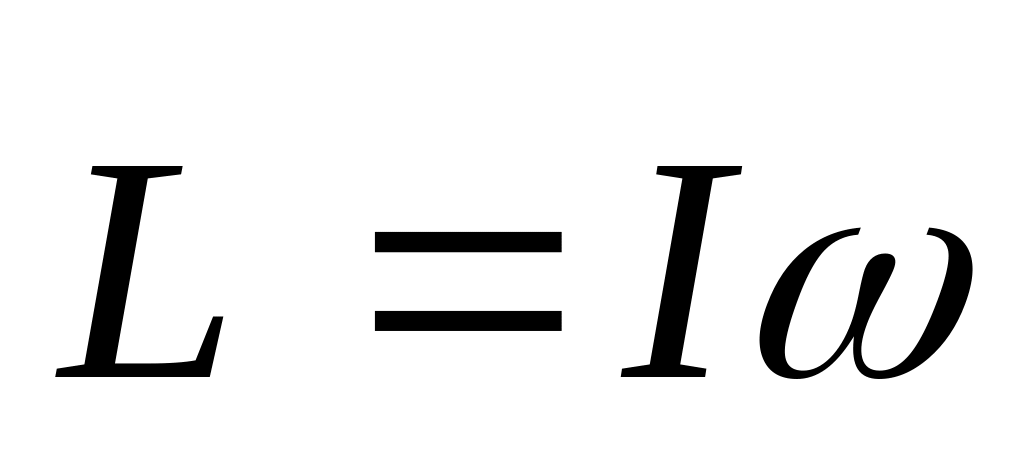 ;
;ось вращения ориентирована вдоль оси , т.е.
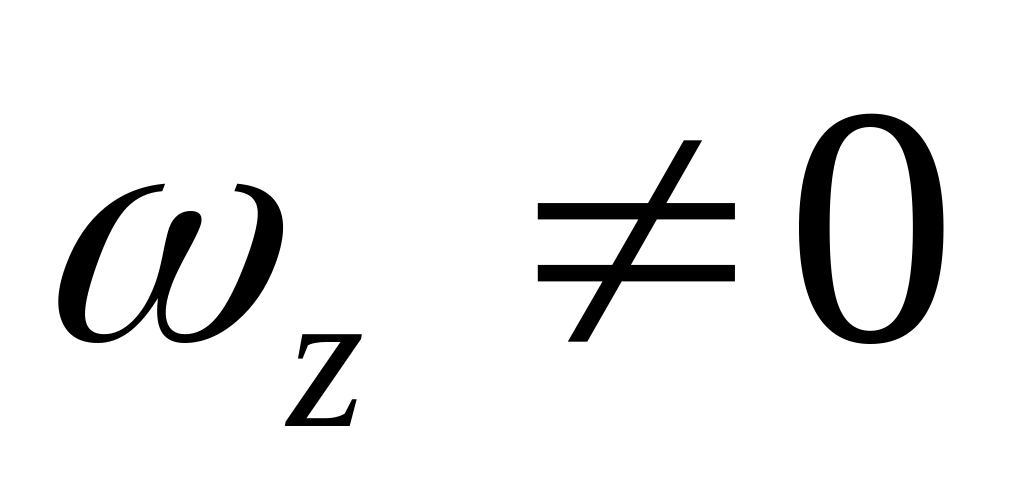 ,
а
,
а
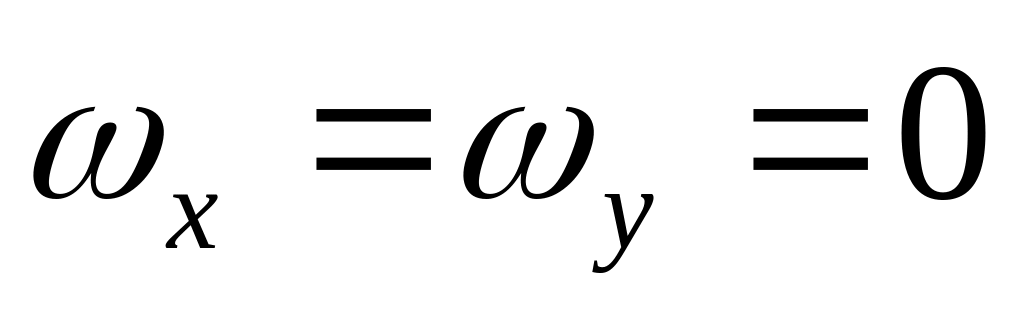 ,
то
,
то
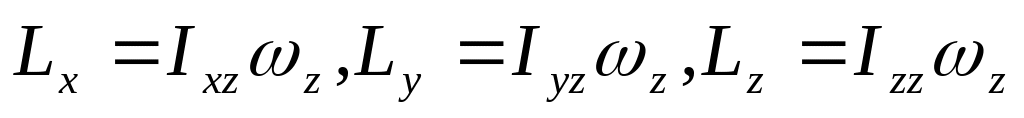 .
.
Совокупность этих
9 величин
![]() тензор 2-го ранга - тензор
инерции:
тензор 2-го ранга - тензор
инерции:
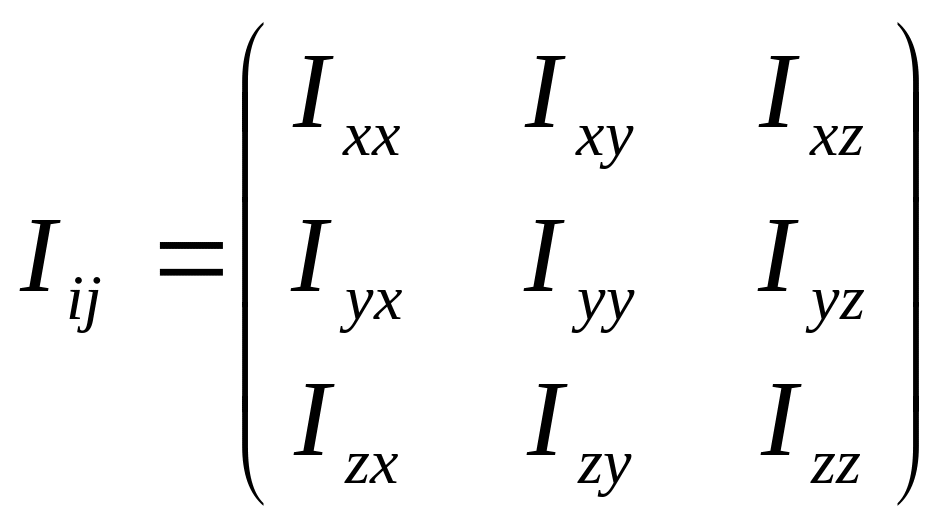 .
(16.15)
.
(16.15)
Операция, определяемая
(16.14), - это умножение вектора
на тензор
![]() ,
в результате чего мы получаем новый
вектор –
.
,
в результате чего мы получаем новый
вектор –
.
Короткая запись уравнений (16.14):
![]()
![]() .
(16.16)
.
(16.16)
Тензор инерции характеризует инертные свойства тела при вращении.
Т.о., для описания
вращательного движения твердого тела
требуется введение новой математической
функции – тензора,
который определяется путем задания
![]() компонент, где
компонент, где
![]() число
измерений пространства,
ранг
тензора,
т.е. в трехмерном пространстве тензор
второго ранга
определяет совокупность девяти величин.
Понятие “тензор” можно распространить
на векторы и скаляры, которые в этом
случае могут быть определены как тензоры
первого и нулевого ранга, соответственно.
число
измерений пространства,
ранг
тензора,
т.е. в трехмерном пространстве тензор
второго ранга
определяет совокупность девяти величин.
Понятие “тензор” можно распространить
на векторы и скаляры, которые в этом
случае могут быть определены как тензоры
первого и нулевого ранга, соответственно.
