20 Л абораторная работа № 1

Лабораторная работа № 1

Обработка прямых многократных равноточных

независимых наблюдений

Цель работы: Изучить методику экспериментальной оценки систематической погрешности средств измерений, способы обнаружения неисключенной систематической погрешности и порядок обработки результатов прямых равноточных многократных наблюдений.

Оборудование рабочего места

Работу выполняют на лабораторном столе, где устанавливаются следующие приборы и оборудование:

• прибор комбинированный Щ4300;

• универсальный вольтметр;

• линейки резисторов.

Теоретические сведения

Для повышения точности измерений часто прибегают к многократным наблюдениям. Причем измерения могут быть как равноточными, то есть выполненными на средствах изме­рения одной точности, так и неравноточными, произведенными на средствах измерения разной точности. Неравноточные из­мерения являются более эффективными для уменьшения сис­тематических погрешностей.

Общая методика экспериментальной оценки систематической погрешности средств измерений.

Оценка проводится в трех точках диапазона: в начале, в середине, в конце. Для определенной точки диапазона оценка производится следующим образом:

1. Обеспечиваются нормальные условия работы средств измерений (СИ).

2. Измеряемая величина подается на оба СИ- рабочее и образцовое, причем случайная погрешность образцового СИ в 3-5 раз меньше случайной погрешности рабочего СИ.

Одновременно измеряются показания образцового X_обр и рабочего СИ X_р.

3. Измерения повторяют N раз.

4. Погрешность i-го наблюдения равна

(1.1)

и содержит в общем случае систематическую и случайную составляющие

. (1.2)

Тогда систематическая погрешность СИ

, (1.3)

так как случайные погрешности имеют разные знаки, поэтому компенсируются:

. (1.4)

Обработка результатов прямых многократных равноточных независимых наблюдений

1. Из результатов измерений исключить известные систематические погрешности:

,

где -результат i-го наблюдения, -поправка в виде систематической погрешности, определяемая по формуле (1.3),

-исправленный результат i-го наблюдения.

2. Проверяется наличие грубых погрешностей. Для этого:

• предварительно определяется математическое ожидание результатов наблюдений:

, (1.5)

где n- количество наблюдений;

• вычисляется среднеквадратическое отклонение результатов наблюдений:

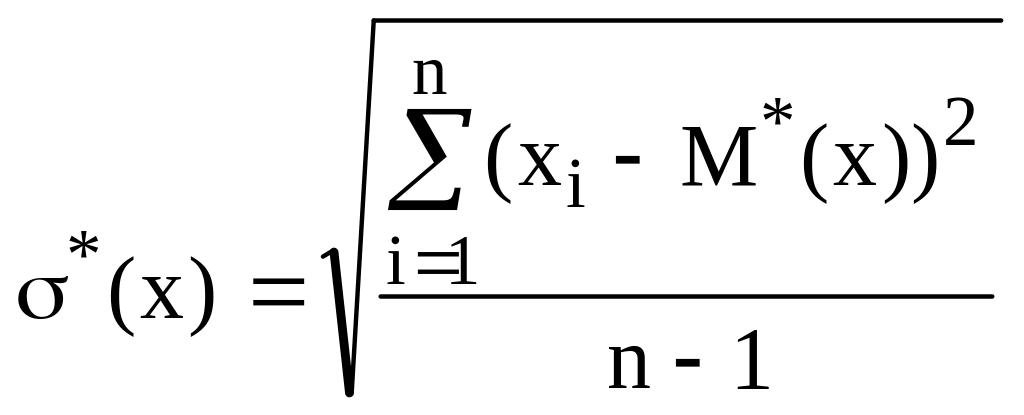; (1.6)

• все результаты измерений располагают в виде вариационного ряда (порядке возрастания или убывания);

• для крайних (подозреваемых) результатов определяют величину t_i:

, (1.7)

затем t_i сравнивают с t_гр, взятым из таблицы для определенного уровня значимости =0,5 (см. прил. 6). Если t _i > t _гр., то результат x _i является грубой погрешностью и его из обработки исключить.

3. Повторяют вычисления математического ожидания результатов наблюдений, принимаемое за точечную оценку результата измерения и среднеквадратическое отклонение результатов наблюдений.

4. Вычисляется среднеквадратическое отклонение результата измерения:

, (1.8)

где n - объем выборки после исключения грубых погрешностей.

5. Проверяется гипотеза о принадлежности результатов наблюдений к нормальному закону распределения. Для проверки гипотезы о принадлежности результатов наблюдений нормальному (или иному распределению) используют различные критерии, область применения которых в основном определяется числом результатов наблюдений n. При n>50 для проверки гипотезы о соответствии нормальному распределению ГОСТ 11.006-74 рекомендует применять критерий Пирсона (его еще называют критерием 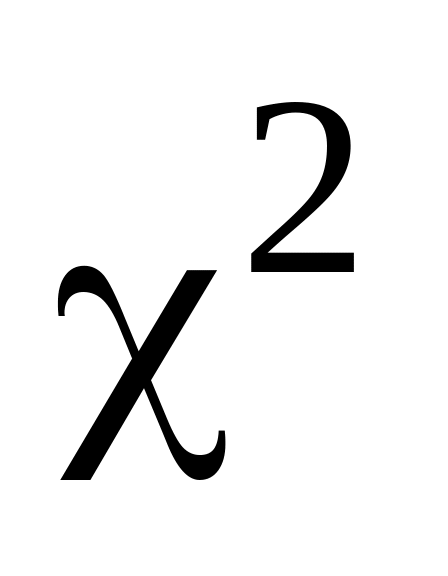) или критерий Колмогорова [2,4]; при 15<n<50 - составной критерий. При n<15 принадлежность результатов наблюдений к нормальному распределению не проверяют. При этом для нахождения доверительных границ случайной погрешности результата измерения используют распределение Стьюдента только в том случае, если заранее известно, что результаты наблюдений принадлежат к нормальному закону распределения.

Для проверки принадлежности к нормальному распределению по критерию Пирсона результаты наблюдений необходимо представить в виде табл. 1.1. Где - количество интервалов. Если n<200, то обычно принимают . Необходимо, чтобы каждый интервал содержал не менее 5 наблюдений, в противном случае малочисленные интервалы объединяют, суммируя число элементов. Если при вычислении m_j, результат наблюдения находится точно на границе двух интервалов, то условно считается, что данное значение принадлежит в равной мере к обоим интервалам и поэтому необходимо к каждому интервалу прибавить 0,5.

Таблица 1.1

Номер интервала	1	2	3	...
Интервалы				...
Число элементов, попавших в j-й интервал (mj)				...
Вероятность pj*=mj/n				...
Теоретическая вероятность

Здесь - количество интервалов. Если n<200, то обычно принимают . Необходимо, чтобы каждый интервал содержал не менее 5 наблюдений, в противном случае малочисленные интервалы объединяют, суммируя число элементов. Если при вычислении m_j, результат наблюдения находится точно на границе двух интервалов, то условно считается, что данное значение принадлежит в равной мере к обоим интервалам и поэтому необходимо к каждому интервалу прибавить 0,5.

_{Теоретическая вероятность попадания результатов} в каждый интервал определяется по формуле

, (1.9)

где x_jн и x_jв - соответственно нижняя и верхняя и границы j-го интервала; f(x) - теоретическая плотность распределения вероятностей, которой сглажена гистограмма.

Для нормального закона распределения вычисления можно упростить, пользуясь формулой

, (1.10)

где Ф (Z)- табулированная функция Лапласа. Ее значения для различных значений аргумента приведены в прил. 1.

После этого вычисляется значение :

. (1.11)

Затем по таблице критических точек распределения (прил. 2) находят критическую точку от заданного уровня значимости g и числа степеней свободы r:

(1.12)

Далее сравнивают полученные результаты. Если , то гипотезу принимают, если , то отвергают.

Составной критерий о принадлежности результатов наблюдений нормальному распределению состоит из двух критериев.

Критерий 1.По результатам наблюдений вычислить отношение

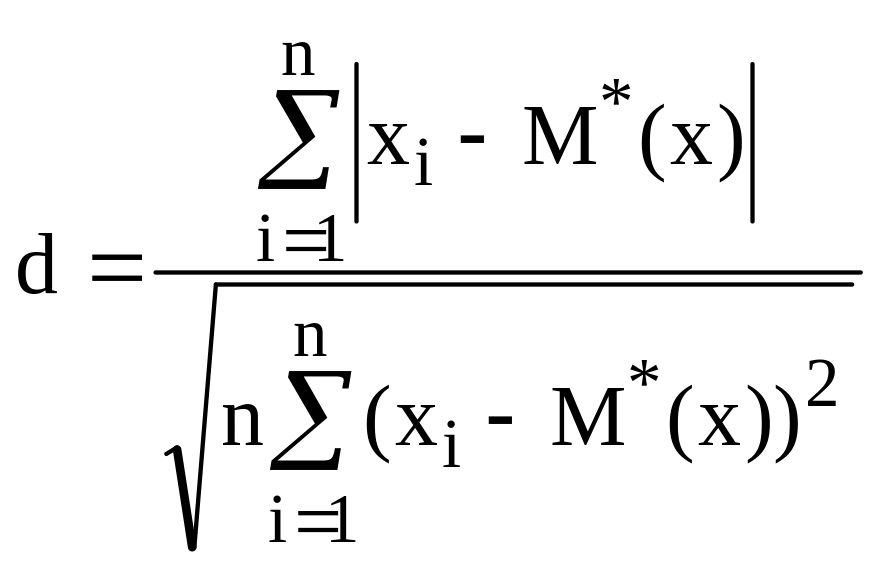, (1.13)

проверить условие:

, (1.14)

где и - процентные точки (квантили) распределения величины , получаемые из таблицы (см. прил. 3) для заранее выбранного уровня значимости =5% и количества наблюдений . Если условие выполняется, то гипотеза о нормальности распределения по критерию 1 не отвергается, в противном случае - гипотеза отвергается.

Критерий 2. Этот критерий введен дополнительно для проверки "концов" распределения. Гипотеза о нормальности распределения по критерию 2 принимается, если количество разностей , превосходящих , будет не более , где r - число степеней свободы [см. формулу (16)]; - верхняя квантиль (процентная точка) нормированной функции Лапласа, соответствующая вероятности P, которая определяется по таблице (прил. 5) по выбранному уровню значимости и числу наблюдений .

Если число разностей , больших , превышает , то гипотеза отвергается.

Гипотеза о нормальности распределения по составному критерию принимается, если выполняются оба критерия. Результирующий уровень значимости составного критерия:

. (1.15)

Величина устанавливается в пределах от 2% до 10%.

6. Находятся границы доверительного интервала случайной погрешности результатов измерений. Доверительный интервал

,

где t - коэффициент, зависящий от доверительной вероятности Р и объема выборки.

При заданной вероятности P величину t определяют законом распределения. Для определения доверительного интервала доверительную вероятность Р принимают равной 0,95. В случаях, когда измерения повторить нельзя и они связаны с созданием эталонов и здоровья людей, Р=0,99.

Для нормального закона при t выбирается по таблицам Лапласа, при в качестве t берется коэффициент распределения Стьюдента (см. прил. 4). Тогда интервал определяется

. (1.16)

7 Определяются границы неисключенной систематической погрешности (НСП). Обнаруживаются НСП одним из следующих способов:

• проведением измерений другим методом и сравнением результатов;

• резким изменением условий наблюдения (использование других экземпляров средств измерений, смена оператора, изменение времени наблюдения, например проведение в ночное время, когда выключено все технологическое оборудование);

• проведением контрольного измерения в лаборатории другого предприятия с более точными системами измерения и методиками выполнения измерений;

• теоретической оценкой НСП, используя другие модели, объекты измерения, методы и системы измерения.

Для определения границ неисключенной систематической погрешности при m<4 пользуются формулой

, (1.17)

где - границы i-й неисключенной систематической погрешности; m-число измеряемых погрешностей.

8. Находят границы доверительного интервала суммарной погрешности.

Суммарная погрешность результата складывается из случайной составляющей и неисключенной суммарной систематической погрешности .

Если отношение меньше 0.8, то неисключенной систематической погрешностью пренебрегают и в качестве границы погрешности результата измерения принимают .

Если , то пренебрегают случайной погрешностью и .

Если , то учитывают систематическую и случайную погрешности:

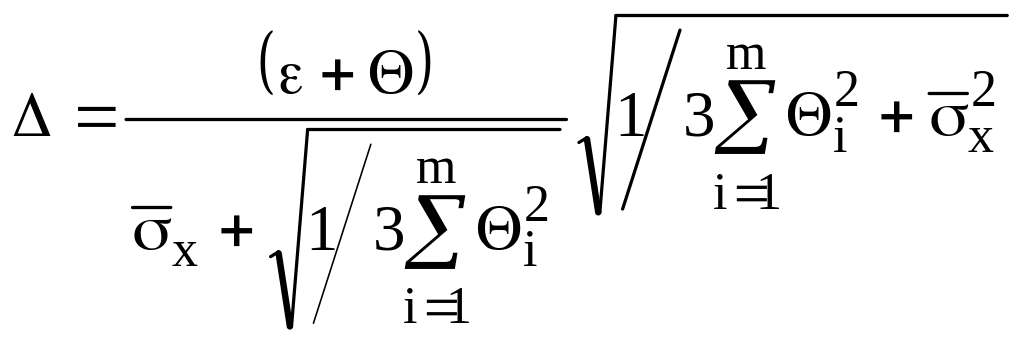(1.18)

С погрешностью не более 10% эта формула заменяется более простой:

, (1.19)

которая считается универсальной для всех видов измерений.

8. Записывается окончательный результат измерений. Существуют следующие формы представления результатов:

1. в виде 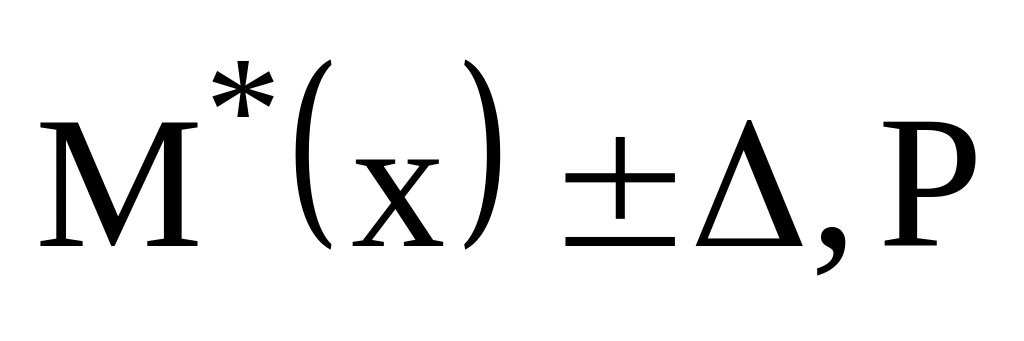- для симметричного доверительного интервала;

2. - для несимметричного доверительного интервала;

3. - если функции распределений составляющих погрешностей неизвестны.

Окончательный результат записывают с учетом правила округления, в соответствии с которым погрешность выражается числом с одной цифрой, если цифра старшего разряда больше трех, или двумя значащими цифрами, если цифра старшего разряда равна трем или меньше трех, а также в случае более точных измерений. Оценка измеряемой величины должна быть записана числом, оканчивающимся цифрой того же разряда, что и интервальная оценка. Поэтому необходимо провести округление результатов по следующему правилу:

• если первая из отбрасываемых цифр больше или равна 5, а за ней есть еще значащие цифры, то последнюю из сохраняемых цифр увеличивают на 1, например: 28,754 - 28,8;

• если отбрасываемая цифра 5, а за ней нет значащих цифр, то последнюю сохраняемую цифру оставляют неизменной, если она четная, и увеличиваю на 1, если она нечетная, например: 28,75 - 28,8; 28.65 - 28.6;

• если первая из отбрасываемых цифр меньше 5, последнюю сохраняемую цифру не изменяют, например:218,74 - 218,7.

Округление производится лишь в окончательном ответе, а все предварительные расчеты выполняются не менее, чем с одним лишним знаком.