Практичне заняття 7. Оптимізація функції однієї змінної у системі matlab

У системі MATLAB є чимало функцій, що реалізують різні методи оптимізації. Вивчимо одну з них, що шукає мінімум дійсної функції однієї дійсної змінної. Відповідна коротка MATLAB-програма наведена нижче.

%*********************************************************************

% Optimization (golden section and parabolic interpolation)

%*********************************************************************

clear;

x=[-pi:0.01:4*pi];

f=sin(x)+x/10;

plot(x,f); grid;

options=optimset('display', 'iter');

[xmin,fmin,exitflag,output]=fminbnd('sin(x)+x/10', 0, 4*pi, options),

MATLAB-програма після очищення робочої області пам’яті будує графік функції мети f за значеннями аргумента в масиві x від –π до 4π з кроком 0.01 (рис. 22).

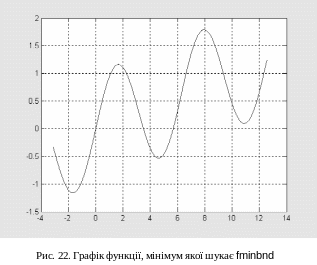
Далі йде звертання до функції MATLAB fminbnd. Ця функція надійно знаходить мінімум дійсної функції дійсного аргумента за комбінованим методом, що спочатку звужує інтервал пошуку методом „золотого січення”, а потім уточнює рішення інтерполяційним параболічним методом.

Чотирма аргументами функції fminbnd є: стрічковий вираз, що задає функцію мети; нижня та верхня початкові межі інтервалу пошуку; масив параметрів оптимізації, заданий функцією optimset у попередньому операторі програми. Функція optimset задає вивід у командне вікно MATLAB результатів усіх ітерацій пошуку мінімума з методом пошуку на кожному кроці (дивись таблицю 2).

Кінцеві результати пошуку виводить в командне вікно функція fminbnd в наступному порядку: значення аргумента у точці мінімума xmin; значення функції мети у точці мінімума fmin; логічна змінна результатів пошуку exitflag; підсумкові параметри пошуку output (кількість ітерацій, кількість обчислень функції мети, назва методу оптимізації).

Лабораторна робота 7. Оптимізація функції однієї змінної у системі matlab

1.  Набрати в системі MATLAB та відлагодити текст програми оптимізації функції однієї змінної.

2.  Підібрати такі значення нижньої межі початкового відрізка, за якого ітераційний процес пошуку мінімума збігається до локального чи глобального мінімума (рисунок 22). Відзначити кількість ітерацій в кожному випадку та перебіг ітераційного процесу (таблиця 2).

3.   Пояснити всі оператори MATLAB-програми.

Нижня межа початкового відрізка пошуку мінімума є другим аргументом функції fminbnd. Залежно від значення цієї нижньої межі функція fminbnd знаходить або локальні мінімуми з координатами (10.8954, 0.0946) та (4.6122, -0.5338), або глобальний мінімум з координатами (-1.6710, -1.1621) (дивись таблицю 2).

Треба задавати різні значення другого аргумента і слідкувати за кординатами мінімума (xmin, fmin), який знаходить функція fminbnd. Достатньо зафіксувати які-небудь три значення нижньої межі, що відповідають трьом мінімумам.

Таблиця 2. Вивід результатів пошуку мінімума функції sin(x)+x/10, якщо початковий інтервал пошуку [0, 4*pi].

Func-count x f(x) Procedure

1 4.79993 -0.516178 initial

2 7.76644 1.77282 golden

3 2.96652 0.470834 golden

4 4.86953 -0.500727 parabolic

5 4.55691 -0.532246 parabolic

6 3.94943 -0.327853 golden

7 4.61212 -0.533765 parabolic

8 4.61209 -0.533765 parabolic

9 4.61222 -0.533765 parabolic

10 4.68392 -0.531203 golden

11 4.61219 -0.533765 parabolic

12 4.61226 -0.533765 parabolic

Optimization terminated successfully: the current x satisfies the termination criteria using OPTIONS. TolX of 1.000000e-004

xmin = 4.6122

fmin = -0.5338

exitflag = 1

output = iterations: 9 funcCount: 9 algorithm: 'golden section search, parabolic interpolation'

Контрольні завдання до розділу 7

1. В чому відмінність безумовних та умовних задач оптимізації?

2. Чому поєднують методи „золотого січення” та інтерполяційний?

3. Поясніть градієнтний метод та метод найшвидшого спуску.

Розділ 8. Умовна оптимізація. Лінійне програмування.

Розглянемо деякі методи розв’язування умовних задач оптимізації.

Розв’язування задач оптимізації з обмеженнями значно складніше, ніж розв’язування безумовних задач. На початку попереднього розділу наведено задачу пошуку паралепіпеда з мінімальною поверхнею, де вдалось за рахунок рівняння-обмеження зменшити кількість параметрів оптимізації та звести задачу до безумовної. Однак такі прості рішення можливі у виняткових випадках.

Поширеним є метод штрафних функцій, що зводить умовну задачу до безумовної.

Нехай умовна задача оптимізації полягає в пошуку мінімума функції векторного аргумента , причому повинні виконуватись обмеження-рівності а також обмеження-нерівності . Функцію мети доповнимо такою додатковою штрафною функцією, щоб мінімізація доповненої функції мети враховувала обмеження. Покажемо це на прикладі такої доповненої функції мети:

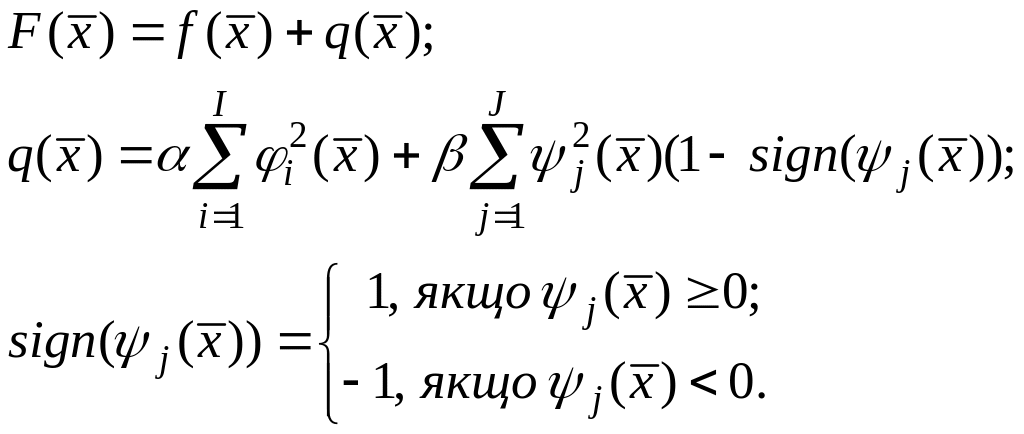
Функція – штрафна. Легко бачити, що штрафна функція рівна 0, якщо виконуються обмеження-рівності та обмеження-нерівності. Разом з тим штрафна функція більша нуля, якщо хоча б одне обмеження не виконується, тобто на доповнену функцію мети накладається штраф за невиконання обмежень. Розмір штрафа залежить від коефіцієнтів α>0 та β>0. Таким чином, безумовний мінімум доповненої функції мети досягається лише за умови виконання обмежень, врахованих штрафною функцією.

Важливими є такі задачі умовної оптимізації, де функція мети та обмеження лінійно залежать від вектора параметрів, тобто задачі лінійного програмування. Почнемо з прикладу такої задачі.

Підприємство має запаси трьох видів сировини: A – 300 одиниць; B – 280 одиниць; C – 300 одиниць. З цієї сировини виробляють два види продукції. Для виробництва одиниці першої продукції треба 5 одиниць сировини A, 4 одиниці сировини B та 3 одиниці сировини C. Виробництво одиниці другої продукції потребує 3 одиниці A, 4 одиниці B та 5 одиниць C. Позначимо x₁ та x₂ кількість виробів першої та другої продукції. Оскільки запаси сировини обмежені, маємо обмеження-нерівності за кожним видом сировини:

5x₁+3x₂≤300; 4x₁+4x₂≤280; 3x₁+5x₂≤300. (8.1)

Крім того, підприємство тільки виробляє, а не споживає продукцію:

x₁≥0; x₂≥0. (8.2)

Нехай треба скласти такий виробничий план, щоб загальна вартість виробленої продукції було найбільша. Якщо вартість одиниці першої продукції 3, а другої – 2, тоді маємо:

f = 3x₁+2x₂ → max. (8.3)

Максимізація функції мети (8.3) (або мінімізація –f ) з обмеженнями (8.1) і (8.2) – це типова задача лінійного програмування з двома параметрами оптимізації та п’ятьма нерівностями-обмеженнями.

У загальному випадку задача лінійного програмування може мати наступне формулювання. Задані коефіцієнти та . Треба знайти таке значення вектора параметрів , яке відповідає максимуму функції мети 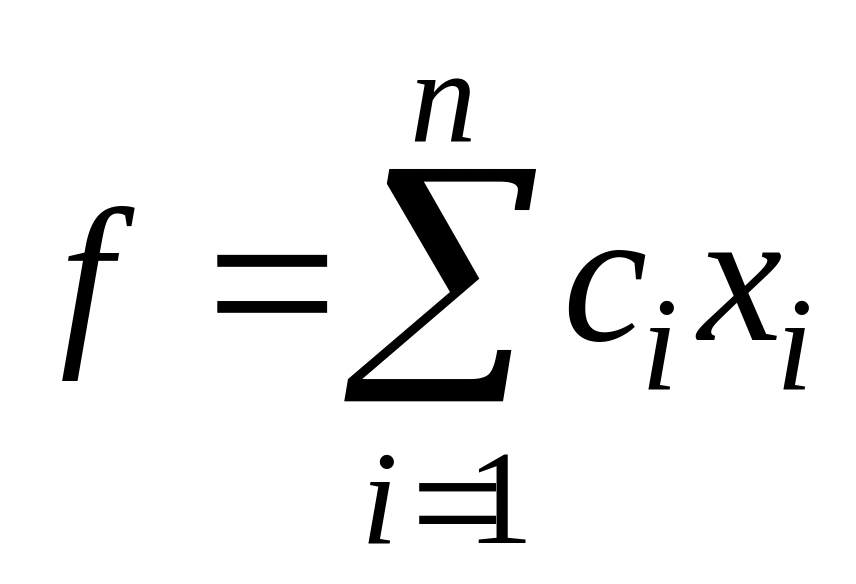з врахуванням обмежень 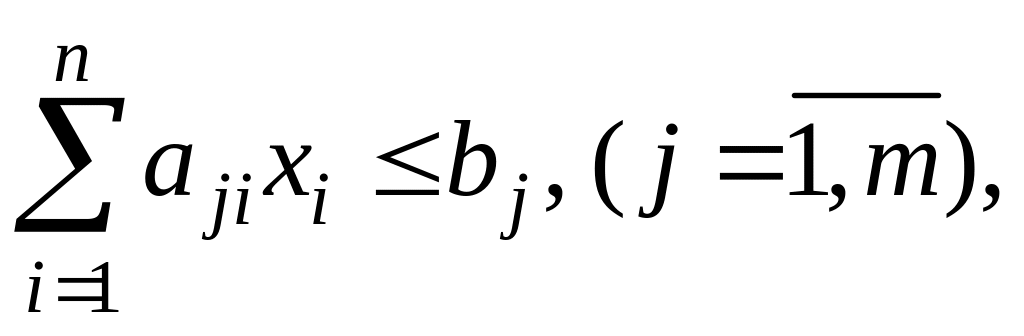та .

Розглянемо графічну інтерпретацію двовимірної задачі лінійного програмування (8.1)-(8.3).

Кожна з нерівностей-обмежень (8.1) може бути зображена у площині (x₁, x₂) півплощиною, гранична пряма якої задана відповідною рівністю. Наприклад, для першої нерівності (8.1) рівняння граничної прямої 5x₁+3x₂=300 зображене відповідною прямою на рис. 23, що проходить через точки (0, 100) та (60, 0). Сірою штриховкою позначена та з півплощин, для точок якої не виконується нерівність 5x₁+3x₂≤300. Ще двома прямими з відповідною штриховкою зображені на рис. 23 решта нерівностей (8.1).

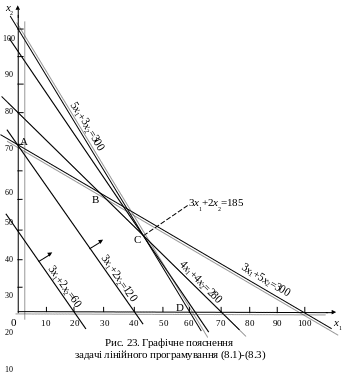
Граничні прямі для нерівностей (8.2) співпадають з координатними осями: для осі абсцис x₂=0; для осі ординат x₁=0. Отже, для точок півплощини зліва від осі ординат не виконується перша нерівність (8.2), а для півплошини під віссю абсцис – друга нерівність. Відповідна штриховка осей координат зображає це.

Отже, всі п’ять нерівностей-обмежень (8.1)-(8.2) зображені на рис. 23 відповідними граничними прямими зі штриховкою „заборонених” півплощин. Яка ж область буде „дозволеною” для всіх обмежень? Неважко помітити, що для п’ятикутника 0ABCD, вершини якого є точками попарних перетинів граничних прямих, всі штриховки є зовнішніми. А значить, для всіх точок всередині цього п’ятикутника включно з його границями виконуються всі п’ять нерівностей-обмежень (8.1)-(8.2). Таку область називають областю допустимих розв’язків. Шуканий оптимальний розв’язок повинен належати цій області.

Звернемось тепер до функції мети (8.3). На рис. 23 ліва жирна пряма зображає функцію мети зі значенням 60, тобто координати кожної точки цієї прямої задовольняють рівняння 3x₁+2x₂=60. Вектор, перпендикулярний до цієї прямої, вказує напрям переміщення зображуючої прямої, якщо значення функції мети зростає. Так, наступна жирна пряма зображає функцію мети, якщо її значення 120. Подальше переміщення прямої зі збільшенням значення триває до границі області допустимих розв’язків. З рис. 23 очевидно, що найбільшого допустимого значення 185 функція мети досягає у вершині С, координати якої (45, 25) є сумісним розв’язком рівнянь 5x₁+3x₂=300 та 4x₁+4x₂=280. Отже, розв’язок (x₁=45, x₂=25) є шуканим оптимальним виробничим планом.

Для задач лінійного програмування доведено, що область допустимих розв’язків є багатовимірним опуклим багатогранником у просторі параметрів, а максимальне значення функції мети, якщо воно існує, досягається хоча б в одній вершині цього багатогранника. Звідси випливає метод розв’язування: треба переглянути вершини багатогранника допустимих розв’язків і вибрати ту, де значення функції мети найбільше.

Саме такий метод з деякими вдосконаленнями вперше запропонував знаменитий радянський математик і економіст Леонід Віталієвич Канторович у 1939 році в книзі, де були сформульовані та розв’язані задачі лінійного програмування переважно для економічних проблем. Незалежно від нього американський математик Джордж Данціг (Dantzig) у 1947 році не лише повторив результати Канторовича, але й запропонував метод цілеспрямо­ваного перебору вершин багатогранника допустимих розв’язків, щоб функція мети не зменшувалась. Симплекс-метод Данціга виявився дуже цінним, бо кількість параметрів і обмежень практичних задач лінійного програмування може сягати багатьох тисяч, і оглянути всі вершини неможливо навіть з потужною обчислювальною технікою. Згодом американський економіст нідерландського походження Тьялінг Купманс (Koopmans) розвинув теорію та економічну інтерпретацію задач, які саме він вперше назвав лінійним програмуванням.

До задач лінійного програмування зводиться багато практично важливих задач оптимізації та прийняття рішень, особливо економічних та військових. Тому Канторович і Купманс у 1975 р. стали лауреатами Нобелівської премії у галузі економіки.

Зараз програми розв’язування різних задач лінійного програмування є обов’язковою складовою всіх універсальних систем програмування і широко використовуються в різноманітних галузях знань.