Практичне заняття 8. Розв’язування задачі лінійного програмуван ня в системі matlab

На практичному занятті вивчимо MATLAB-програму, що розв’язує нескладну тривимірну задачу лінійного програмування.

Нехай треба знайти максимум функції мети f = 5x₁+4x₂+6x₃ (або міні­мум функції мети f = –5x₁–4x₂–6x₃) за умови виконання шести обмежень-нерівностей x₁–x₂+x₃≤20, 3x₁+2x₂+4x₃≤42, 3x₁+2x₂≤30, x₁≥0, x₂≥0, x₃≥0.

Цю задачу можна записати в сучасному матричному вигляді:

де

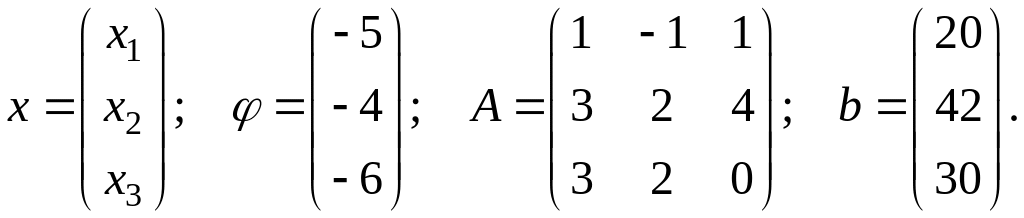
Оцінимо загальну кількість вершин багатогранника області допустимих розв’язків. Шість рівнянь граничних площин такі: x₁–x₂+x₃=20; 3x₁+2x₂+4x₃=42; 3x₁+2x₂=30; x₁=0; x₂=0; x₃=0. Оскільки параметрів три, то координати вершин повинні бути розв’язками хоча б трьох рівнянь з перелічених. Кількість комбінацій з 6 по 3 рівна 20. Насправді кількість вершин менша, бо деякі розв’язки можуть суперечити обмеженням, тобто виходити за межі допустимого багатогранника.

Отже, треба знайти серед 20 розв’язків такі, що не суперечать обмеженням, тобто є координатами вершин допустимого багатогранника, та вибрати такий розв’язок, для якого значення функції мети найбільше (найменше). Виглядає громіздко навіть для такої простої задачі.

Текст MATLAB-програми, що розв’язує цю задачу симплекс-методом, наведено нижче.

%********************************************************************

% Linear programming problem resolution:

% search min(φ^Tx) such that Ax≤b & x≥lb

%*********************************************************************

φ = [-5; -4; -6];

A = [1 -1 1; 3 2 4; 3 2 0];

b = [20; 42; 30];

lb = zeros(3,1);

[x,φopt,exitflag,output] = linprog(φ, A, b, [ ],[ ], lb)

Перший оператор програми задає коефіцієнти функції мети у векторі φ. Далі задані матриця A та вектор правих частин b трьох перших нерівностей-обмежень. Четвертий оператор задає нульовий вектор-стовпець lb для решти нерівностей-обмежень. Далі йде звертання до MATLAB-функції linprog, яка розв’язує задачу лінійного програмування модифікованим симплекс-методом. Аргументами функції linprog є φ, A, b, а також lb після двох пустих позицій [ ],[ ]. Результати обрахунків виводяться в командне вікно MATLAB у такому порядку: вектор оптимального розв’язку x; відповідне значення функції мети φopt; логічна змінна завершення пошуку exitflag; вектор деяких параметрів пошуку output.

Лабораторна робота 8. Розв’язування задачі лінійного програмуван­ня у системі MATLAB

1.  Набрати в системі MATLAB та відлагодити текст програми, що розв’язує задачу лінійного програмування.

2.  Переконатись, що отриманий розв’язок є вершиною багатогранника допустимих розв’язків, тобто є розв’язком певних трьох рівнянь граничних площин і не суперечить нерівностям-обмеженням.

3.  Пояснити всі оператори MATLAB-програми.

Контрольні завдання до розділу 8

1. Викладіть метод штрафних функцій.

2. Поясніть, чому область допустимих рішень у двопараметричній задачі лінійного програмування є опуклим багатокутником.

3. Чому екстремум знаходиться в одній з вершин області допустимих рішень?

Розділ 9. Розв’язування звичайних диференціальних рівнянь

Дуже багато проблем і задач природничих, технічних і гуманітарних областей людського знання описують диференціальні рівняння. Тому вміти складати і розв’язувати диференціальні рівняння – значить володіти потужним засобом прийняття обгрунтованих рішень.

Диференціальні рівняння поділяють на два типи – звичайні та в частинних похідних. Звичайні диференціальні рівняння містять одну незалежну змінну, як правило, час. Приклад – другий закон Ньютона, де переміщення залежить лише від часу. Диференціальні рівняння в частинних похідних мають кілька незалежних змінних, тому похідні за кожною змінною зокрема називають частинними. Наприклад, миттєве значення електро­магнітного сигналу в довгій лінії залежить не лише від часу, але й від координати вздовж лінії. Тому рівняння довгої лінії є диференціальним рівнянням у частинних похідних.

Нагадаємо деякі властивості звичайних диференціальних рівнянь. Почнемо з рівняння першого порядку, розв’язаного відносно похідної:

dy/dt = f(y(t)); (9.1)

де: t – незалежна змінна, час; dy/dt – похідна функції y(t); f – деяка задана нелінійна функція.

Розв’язок диференціального рівняння (9.1) – це така функція y(t), підстановка якої разом з похідною до рівняння (9.1) перетворює його в тотожність. Наприклад, для лінійного рівняння dy/dt = –2y розв’язком є функція y(t) = Ce^–2t, похідна якої dy/dt = –2Ce^–2t. Константу С можна визначити з початкової умови y(0)=a₀.

Загальний розв’язок рівняння (9.1) містить довільну константу С.

Знаменитий французький математик Огюстен Коші (Augustin Cauchy) був надзвичайно плідним вченим першої половини 19-го сторіччя. Йому належить біля 800 наукових праць. Зокрема, він довів теорему про існування єдиного часткового розв’язку рівняння (9.1), якщо задано С і виконано умови неперервності функції f(t, y(t)) та її похідної.

Звичайне диференціальне рівняння n-го порядку має такий вигляд:

F(y(t), dy/dt, d²y/dt²,…, dⁿy/dtⁿ)=0, (9.2)

де: t – час; dⁱy/dtⁱ – i-та похідна функції y(t); F – деяка задана функція.

Коші запропонував записувати рівняння (9.2) у формі системи n рівнянь першого порядку, розв’язаних відносно похідних (рівняння у формі Коші):

dy_j/dt = f_j(y₁(t),…, y_n(t)); (j=1,…,n); (9.3) де y₁(t)=y(t) з (9.2).

Загальні розв’язки рівнянь (9.2) і (9.3) містять вже n довільних констант, які можна визначити з n початкових умов: dⁱy(0)/dtⁱ=a_і; і=0,...,n-1; для рівняння (9.2) або y_і(0)=a_і; і=1,...,n; для рівняння (9.3). Доведено аналог теореми Коші про існування єдиного розв’язку рівнянь (9.2) і (9.3).

Аналітично, у вигляді формул, можна знайти розв’язки лише лінійних звичайних диференціальних рівнянь та окремих простих нелінійних. Використовують різноманітні наближені методи аналітичного розв’я­зу­ван­ня, що грунтуються на спрощеннях нелінійних диференціальних рівнянь, перш за все їх лінеаризації. Однак наближені методи мають обмежене засто­су­ван­ня та їхні похибки складно контролювати. Дотепер також застосовують для розв’язування диференціальних рівнянь аналогові обчислювальні машини, засновані на дослідженні перехідних процесів у електричних ана­логах диференціальних рівнянь. Але точність аналогових машин невисока.

З поширенням цифрових ЕОМ загальновживаними стали числові методи розв’язування диференціальних рівнянь. Пояснимо ідею числового розв’язування на прикладі рівняння першого порядку (9.1).

Будь-яка цифрова ЕОМ працює дискретно у часі, тобто сприймає дані та видає результати лише в певні моменти часу. Як наслідок всі функції, що використовує ЕОМ, повинні бути дискретизовані. Наприклад, для диференціального рівняння (9.1) функцію неперервного аргумента f(y(t)) замінює функція дискретного аргумента f(y(t_k)), де k – номер часового відліку. Відповідну заміну можна зробити для похідної dy/dt. Згідно з другою формулою з (5.5), dy(t_k+1)/dt≈(y(t_k+1)–y(t_k))/h, де h=t_k+1–t_k – крок за часом. Отже, дискретизоване рівняння (9.1) може мати вигляд

(y^(k+1)–y^(k))/h=f^(k), (9.4)

де y^(k+1)=y(t_k+1), y^(k)=y(t_k), f^(k)=f(y(t_k)).

Рівняння (9.4) називають різницевим. Зазвичай його записують розв’язаним відносно y^(k+1):

y^(k+1)=y^(k)+hf^(k); y⁽⁰⁾=a₀. (9.5)

За формулою (9.5) можна послідовно обрахувати всі дискретні значення функції y^(k), починаючи з y⁽⁰⁾=a₀, тобто знайти дискретний розв’язок рівняння (9.1). Звичайно, цей розв’язок є наближеним, бо заміна похідної різницевим відношенням є наближеною. Але дуже заманливо замість розв’язування нелінійного диференціального рівняння (9.1) багатократно обчислити формулу (9.5). А похибку наближення можна як завгодно зменшити, зменшуючи крок h.

Метод числового розв’язування за формулою (9.5) називають методом Ейлера.

Леонард Ейлер (Leonhard Euler) – великий математик, фізик, механік, астроном 18-го сторіччя. Швейцарського походження, у 19 років він переїхав до Росії, де надзвичайно плідно працював у Санкт-Петербурзькій академії наук все життя, крім 25-річної перерви на користь Берлінської академії наук. Ейлеру належить майже 900 наукових публікацій у найрізноманітніших галузях знань. Ще дотепер триває публікація повного зібрання його творів.

Розглянемо графічне пояснення метода Ейлера. На рис. 24 зображено один крок за методом Ейлера (9.5). Крива лінія – це точний розв’язок рівняння (9.1). Якщо значення y_k відоме, то y_k+1 складається з y_k та добавки δy_k. Тангенс кута нахилу дотичної в точці (x_k, y_k) чисельно дорівнює похідній у цій точці, тобто f^(k), згідно з (9.4). Значить, у відповідному трикутнику f^(k)=δy_k/h. Отже, δy_k=hf^(k), що повністю відповідає формулі (9.5).

З рис. 24 видно, що розбіжність дотичної і точного розв’язку є джерелом похибки метода Ейлера. Очевидно, похибку можна зробити як завгодно малою, зменшуючи h.

Метод Ейлера (9.5) природньо поширюється на систему рівнянь у формі Коші (9.3):

y_j^(k+1)=y_j^(k)+hf_j^(k); y_j⁽⁰⁾=a_j; (j=1,…,n). (9.6)

Однак метод Ейлера для систем рівнянь (9.6) може зустрітись із суттєвими труднощами під час розв’язування так званих жорстких систем.

Систему рівнянь (9.3) можна лінеаризувати в деякій точці (y₁₀,…, y_n0), тобто розкласти функції f_j(y₁(t),…, y_n(t)); (j=1,…,n); у ряди Тейлора в цій точці та відкинути нелінійні члени розкладів:

dy_j/dt ≈ f_j(y₁₀,…, y_n0) + a_1j∆y₁ + a_2j∆y₂ +…+ a_nj∆y_n; (j=1,…,n); (9.7) де: a_ij = ∂f_j(y₁₀,…, y_n0)/∂y_i; ∆y_і = y_і – y_і0; (i,j=1,…,n).

Матриця A=(a_ij); (i,j=1,…,n); – це якоб’ян, з яким ми вже зустрічались у розділі 6. Нехай λ_k, (k=1,…,n), – власні значення якоб’яна, загалом комплексні. Якщо модулі дійсних частин власних значень якоб’яна |Re{λ_k}| дуже відрізняються, то таку систему диференціальних рівнянь називають жорсткою. Жорсткі системи часто зустрічаються при складанні та розв’язуванні прикладних задач з різних галузей знань.

Щоб похибка розв’язування за методом Ейлера не була надто великою, крок розв’язування має задовольняти обмеження h < 2/max|Re{λ_k}|. Це обмеження для жорстких систем може бути надто обтяжливим, бо крок обрахунку повільних розв’язків є дуже малий, а значить час числового розв’язування надто великий навіть для сучасних швидкодіючих ЕОМ.

Цього недоліка позбавлений неявний метод Ейлера, формула якого для рівнянь (9.3) така:

y_j^(k+1)=y_j^(k)+hf_j^(k+1); y_j⁽⁰⁾=a_j; (j=1,…,n). (9.8)

Система рівнянь (9.8) є вже системою нелінійних алгебричних або трансцендентних рівнянь (дивись розділ 6). Цю систему треба розв’язувати щодо y_j^(k+1); (j=1,…,n) на кожному кроці, що значно ускладнює неявний метод порівняно з явним. Але для неявного метода Ейлера обмеження кроку значно слабше, ніж для явного метода. Тому неявним методом Ейлера можна успішно розв’язувати жорсткі системи.

Явний та неявний методи Ейлера є найпростішими та найменш точними з числових методів розв’язування звичайних диференціальних рівнянь. У минулому столітті спеціалісти з прикладної математики розвинули теорію та створили багато різних методів числового розв’язування звичайних диференціальних рівнянь, що відрізняються головно способами різницевої апроксимації похідних та поділяються на дві великі групи – явні та неявні методи. Серед явних методів найчастіше застосовують метод Рунге-Кутта (Runge-Kutt), а серед неявних – метод Гіра (Gear). Відповідні програми містяться в усіх сучасних системах програмування.