
Приклад розв’язання задачі д.5. Третій рівень складності.
Механічна система складається з вертикальної прямокутної плити, яка рухається вздовж горизонтальних напрямних, і тягаря
D.
Маса плити m1=12
кг,
маса тягаря m2=2
кг. В початковий момент часу (t0=0),
коли швидкість плити u0=2
м/с, тягар під дією внутрішніх сил починає
рухатись по жолобу плити,
який
являє
собою
коло радіуса R
=0,7
м. Під час руху тягаря по жолобу кут
змінюється за законом
![]() рад.
рад.
Тягар D вважати матеріальною точкою.
Дано:
m1=12
кг; m2=2
кг; u0=2
м/с; R=0,7
м;
![]() рад.
рад.
Визначити: x1—переміщення плити за проміжок часу від t0=0 до t1=1 c, u1 і N1—значення швидкості плити і повної нормальної реакції напрямних при t1=1 c.
Розв’язання. Розглянемо механічну систему, що складається з плити і тягаря D, в довільному положенні і прикладемо всі зовнішні сили, які діють на неї: сили ваги і , силу реакції напрямних. Проведемо координатні вісі Oxy так, щоб вісь Oy проходила через точку C0, де знаходився центр мас плити в момент часу t0=0 (рис. 21.15).
Для визначення x1 скористаємось теоремою про рух центра мас механічної системи в проекції на вісь Ox:
![]() .
(1)
.
(1)
Визначимо значення MxC. З формули, яка визначає координату xC центра мас системи, одержимо
![]() (2)
(2)
З рисунка 21.15 видно, що
![]() .
(3)
.
(3)
Тоді
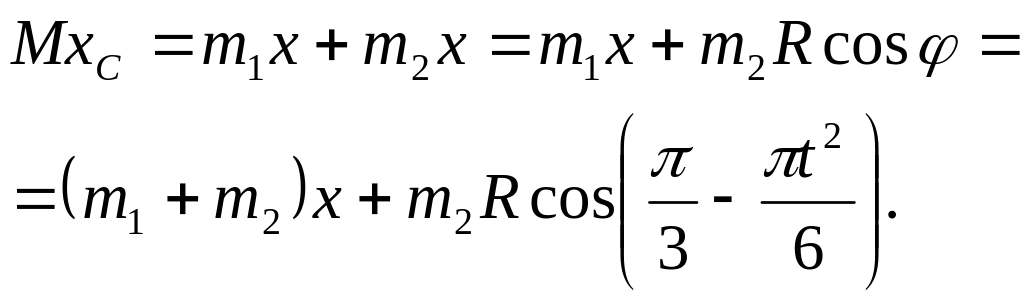 (4)
(4)
Двічі проінтегруємо рівняння (2) і одержимо
![]() ;
;
![]() ,
(5)
,
(5)
де C1 і C2—сталі інтегрування.
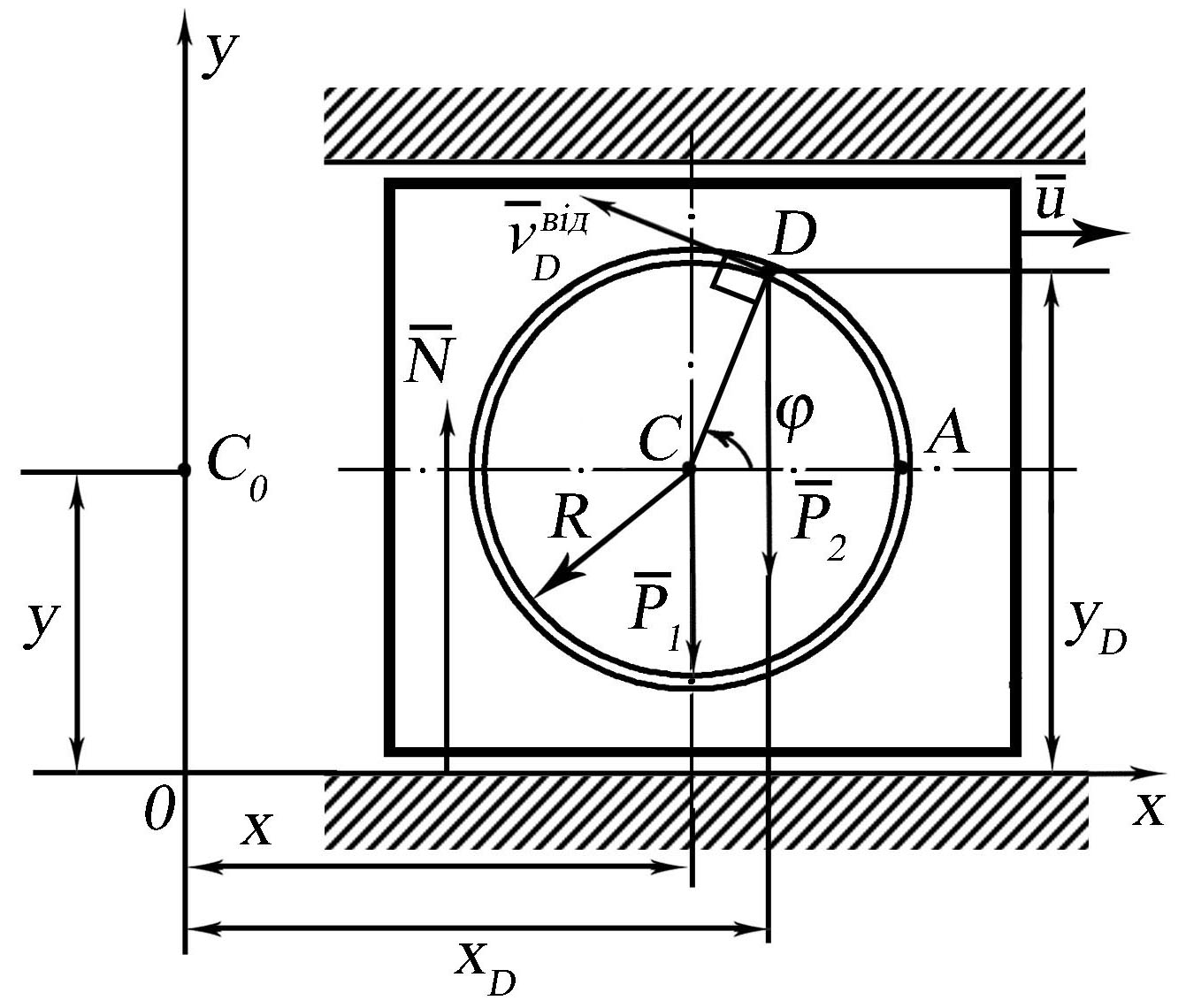
Рис. 21. 15.
Тоді
![]() (6)
(6)
Для визначення C1 і C2 знайдемо ще одне рівняння, яке одержимо, взявши похідну за часом від обох частин рівняння (6):
![]() ,
(7)
,
(7)
де
![]() -
швидкість плити.
-
швидкість плити.
При
t0=0;
x0
=0;
![]() ,тоді
,тоді
![]() ;
;
![]() .
(8)
.
(8)
При цих значеннях С1 і С2 рівняння (6) приймає вигляд
 (9)
(9)
Визначимо залежність координати x від часу t:
![]() (10)
(10)
При t1=1 c
![]()
![]() м.
м.
Для визначення загальної нормальної реакції напрямних скористаємось знову теоремою про рух центра мас системи, але в проекції на вісь Oy :
![]() (1)
(1)
![]() ,
(2)
,
(2)
звідки
![]() . (3)
. (3)
З формули, яка визначає ординату yC центра мас системи одержимо
![]() ,
(4)
,
(4)
тут y—ордината центра ваги плити, yD—ордината тягаря D.
З рисунка 21.15 визначимо, що
;
![]() .
.
Тоді
 (5)
(5)
Візьмемо від обох частин рівняння (5) дві похідні за часом:
![]()
Оскільки
![]() ,
то
,
то
![]() і
і
![]()
![]() (6)
(6)
Тоді
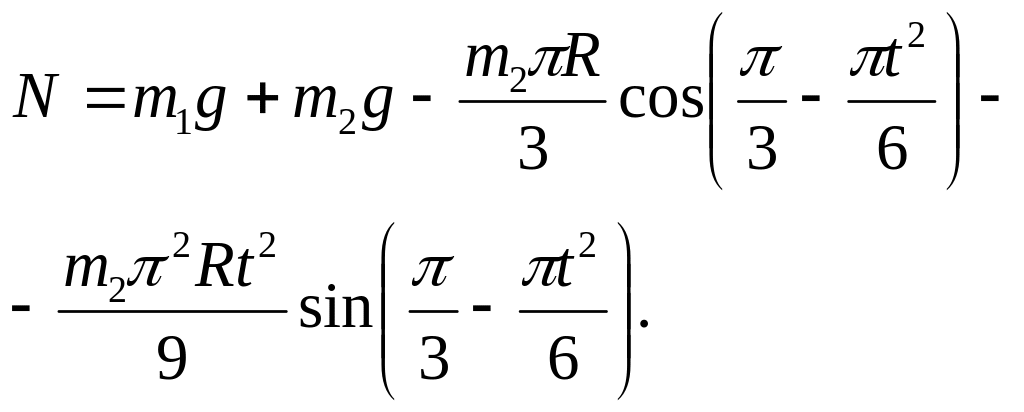 (7)
(7)
При t1 =1 c

![]() Н.
Н.
Для визначення швидкості u1 плити використаємо теорему про зміну кількості руху системи в проекції на вісь Ox:
![]() ;
(1)
;
(1)
![]() .
(2)
.
(2)
Дана механічна система складається з плити та тягаря D, тому
![]() (3)
(3)
Тут
-
кількість руху плити,
![]() - кількість руху тягаря D
.
- кількість руху тягаря D
.
Тягар виконує складний рух. Вважаючи рух тягаря D разом з плитою переносним, а його рух по відношенню до плити (по колу радіуса R)—відносним рухом, для абсолютної швидкості тягаря одержимо
;
. (4)
де
![]() ; направлена швидкість
по дотичній до кола радіуса
; направлена швидкість
по дотичній до кола радіуса
![]() .
.
Тоді
![]() .
.
Переносна швидкість .
Тоді
![]() .
.
Рівняння (2) приймає вигляд
![]() ;
;
![]() .
(5)
.
(5)
При
t0=0
u=u0
і
![]() .
.
Одержимо
![]()
звідки
![]() (6)
(6)
При t1=1 c
![]()
![]() м/с.
м/с.
Відповідь:
![]() м;
м;
![]() м/с;
м/с;
![]() Н.
Н.
Примітка.
При
необхідності визначення прискорення
![]() плити
потрібно скористатись методикою
розв’язання, наведеною в прикладі
першого рівня складності.
плити
потрібно скористатись методикою
розв’язання, наведеною в прикладі
першого рівня складності.
