Задача д.5

Умова задачі. Механічна система складається з прямокутної вертикальної плити 1 маси m₁=20 кг, яка рухається вздовж горизонтальних направляючих, і тягаря D маси m₂=5 кг (рис. Д.5.0—Д.5.9). В момент часу t₀=0, коли швидкість плити u₀=2 м/с, тягар під дією внутрішніх сил починає рухатись по жолобу плити.

На рис. Д.5.0—Д.5.3 жолоб KE прямолінійний і при русі тягаря відстань S=AD змінюється за законом S=f₁(t), а на рис. Д.5.4—Д.5.9 жолоб—коло радіуса R=0,8 м і при русі тягаря кут змінюється за законом , де S виражено в метрах, φ—в радіанах, t—в секундах (таблиця 13. Умови задач Д.5.0—Д.5.9, таблиця 14. Умови задач Д.5.0.А—Д.5.9.А, таблиця 15. Умови задач Д.5.0.Б—Д.5.9.Б).

Вважаючи тягар матеріальної точкою і нехтуючи всіма силами опору, визначити величину (або величини), яка вказана в таблицях 13,14 і 15 в стовпчику „Знайти”, де позначено: x₁ - переміщення плити за час від t₀ =0 до t₁=1 c; u₁, a₁, N₁ - значення в момент часу t₁=1 c відповідно швидкості плити, прискорення плити і повної нормальної реакції направляючих.

Методичні вказівки. Задача Д.5—на застосування теорем про рух центра мас і про зміну кількості руху системи. Першою теоремою зручно користуватись, коли необхідно знайти переміщення або закон руху одного з тіл системи, яке рухається поступально, а другою—коли необхідно знайти швидкість такого тіла. При визначенні прискорення тіла або реакції в’язі також необхідно користуватись першою теоремою.

Теорема про рух центра мас механічної системи записується так:

,

де M—маса системи, - сума проекцій зовнішніх сил на вісь x.

В нашому випадку

і

.

Теорема про зміну кількості руху механічної системи записується так:

,

де Q_x—кількість руху системи в проекції на вісь x.

В нашому випадку

і Q_x=const.

За правильне розв’язання задачі Д.5 з використанням даних таблиці 13. Умови задач Д.5.0—Д.5.9 студент одержує оцінку „задовільно”. За правильне розв’язання задачі Д.5 з використанням даних таблиці 14. Умови задач Д.5.0.А—Д.5.9.А студент одержує оцінку „добре”, а з використанням даних таблиці Д.5.0.Б—Д.5.9.Б—оцінку „відмінно”.

Приклад розв’язання задачі д.5. Перший рівень складності.

Механічна система складається з прямокутної вертикальної плити, яка рухається вздовж горизонтальних напрямних, і тягаря

D. Маса плити m₁=18 кг, маса тягаря m₂=6 кг. В початковий момент часу (t₀=0), коли швидкість плити u₀=3 м/с, тягар під дією внутрішніх сил починає рухатись по жолобу плити, який являє собою коло радіуса R =0,6 м. Під час руху тягаря по жолобу кут змінюється за законом рад.

Тягар вважати матеріальною точкою.

Дано: m₁=18 кг; m₂=6 кг; u₀=3 м/с; R=0,6 м; рад.

1. Визначити: x₁—переміщення плити за проміжок часу від t₀=0 до t₁=1 c.

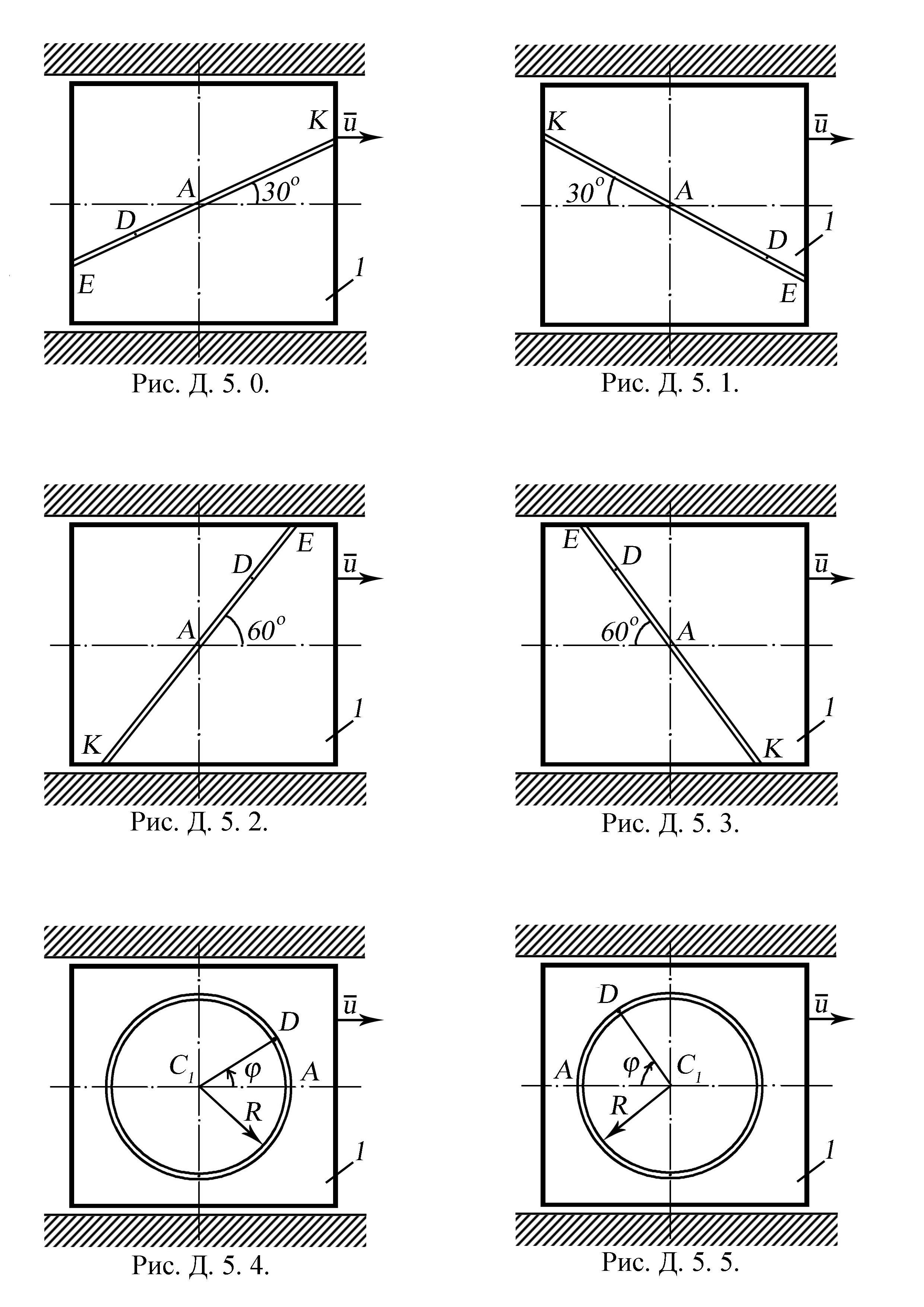
Рисунки до задач Д. 5. 0. – Д. 5. 5.

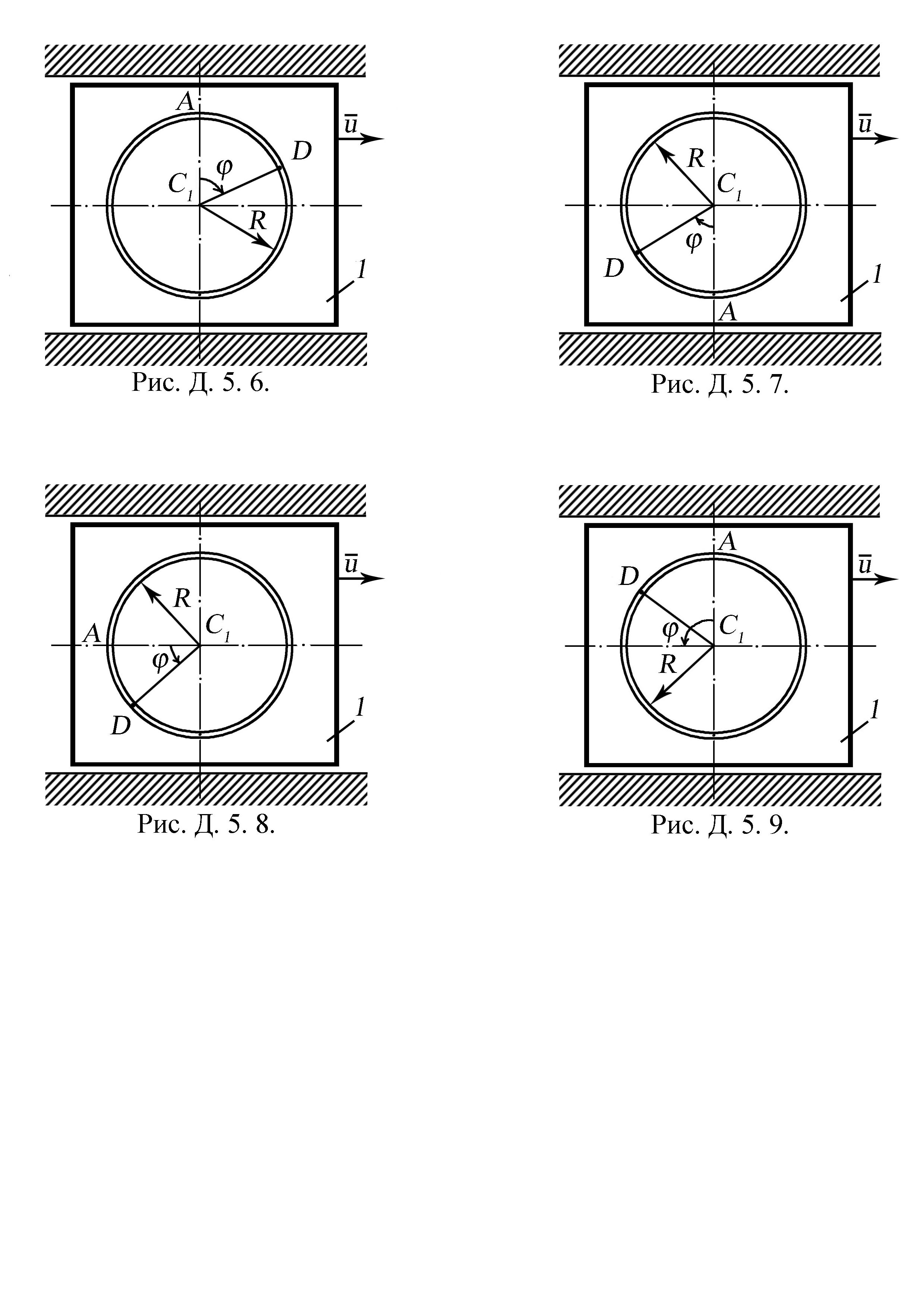
Рисунки до задач Д. 5. 6. – Д. 5. 9.

Розв’язання. Розглянемо механічну систему, що складається з плити та тягаря D, в довільному положенні. Покажемо зовнішні сили, які діють на цю систему: сили ваги і та загальну реакцію напрямних. Проведемо координатні вісі Oxy так, щоб вісь Oy проходила через точку C₀, де знаходився центр мас плити в момент часу t₀=0 (рис. 21.13).

Для визначення x₁ скористаємось теоремою про рух центра мас механічної системи в проекції на вісь Ox:

. (1)

Оскільки в даному прикладі всі діючі зовнішні сили вертикальні, то

і . (2)

Визначимо значення Mx_C. З рис. 21.13 видно, що в довільний момент часу x—абсциса центра мас плити, а x_D –абсциса точки D:

. (3)

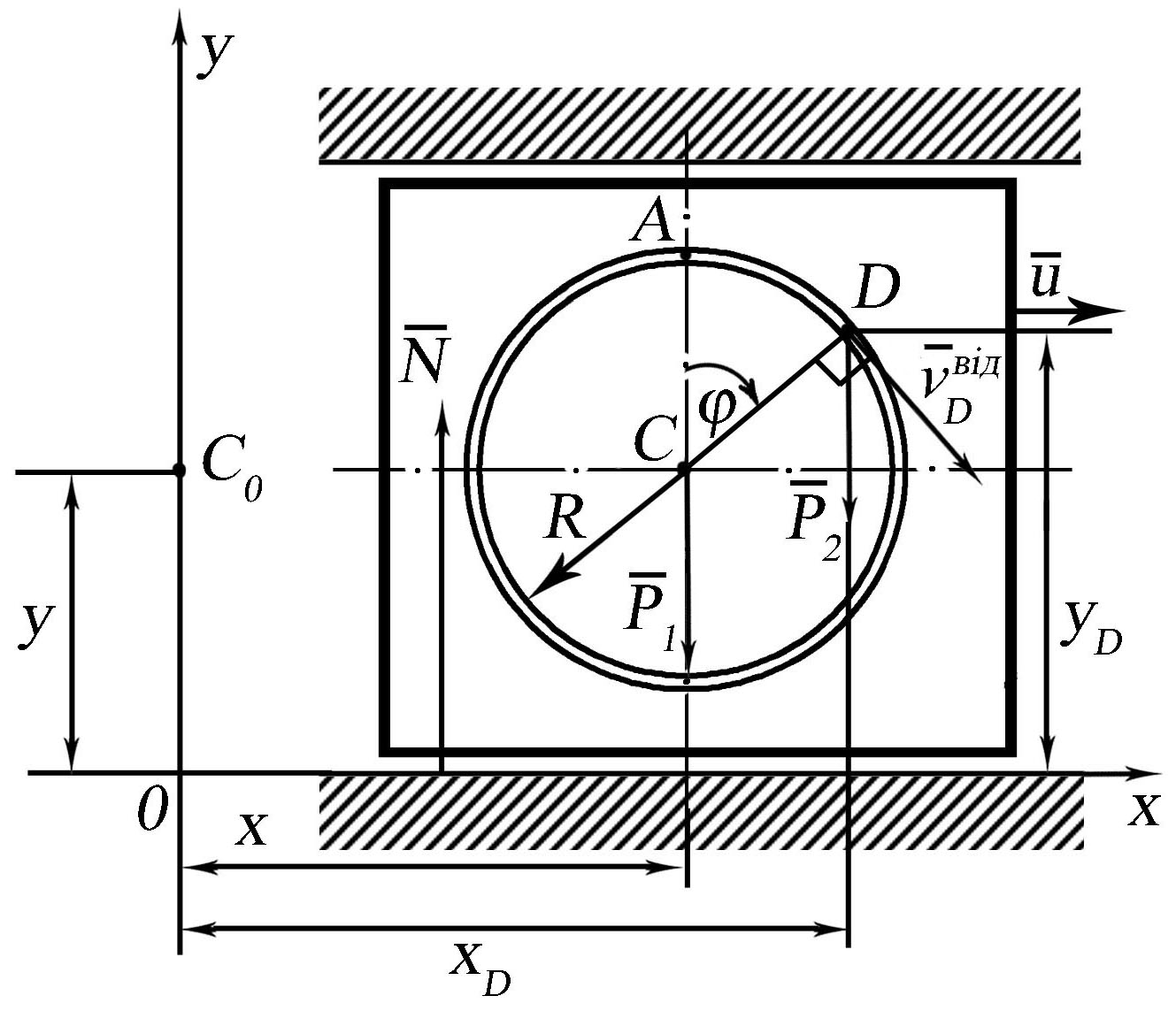
Рис. 21. 13.

З формули, яка визначає координату x_C центра мас системи, одержимо

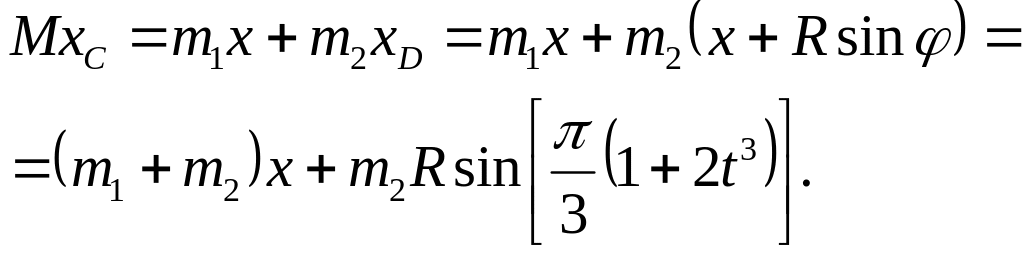(4)

Двічі проінтегруємо рівняння (2) і одержимо, що

; , (5)

де C₁ і C₂—сталі інтегрування.

Тоді

(6)

Для визначення C₁ і C₂ знайдемо ще одне рівняння, яке одержимо, взявши похідну за часом від обох частин рівняння (6):

, (7)

де - швидкість плити.

Запишемо початкові умови руху: при t₀=0; x₀ =0; .

Підставимо ці умови в рівняння (6) і (7) і знайдемо, що

;

. (8)

При цих значеннях С₁ і С₂ рівняння (6)приймає вигляд

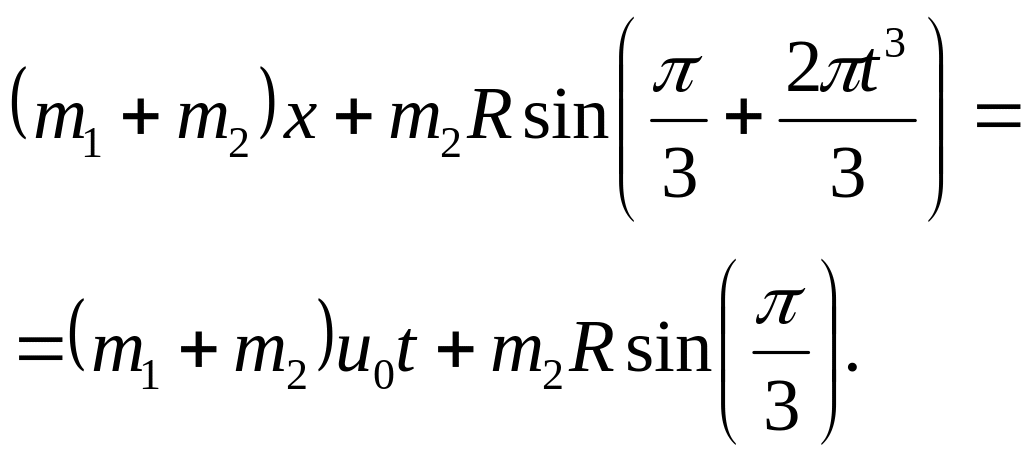(9)

Звідси визначимо залежність координати x від часу t:

(10)

При t₁=1 c

м.

Відповідь: x₁=3,13 м.

2. За тих же умов визначимо a₁—значення прискорення плити при t₁=1 c.

Розглянемо механічну систему в довільному положенні і покажемо всі діючі на неї зовнішні сили (рис. 21.13).

Для визначення a₁ скористаємось теоремою про рух центра мас системи

Повторивши всі міркування і дії, викладені в попередньому пункті розв’язання задачі (при знаходженні переміщення x плити), знайдемо, що

(2)

Для визначення a₁ візьмемо від рівняння (2) дві похідні за часом:

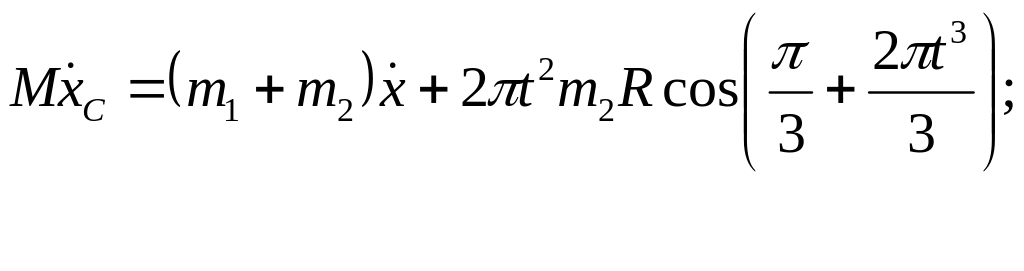
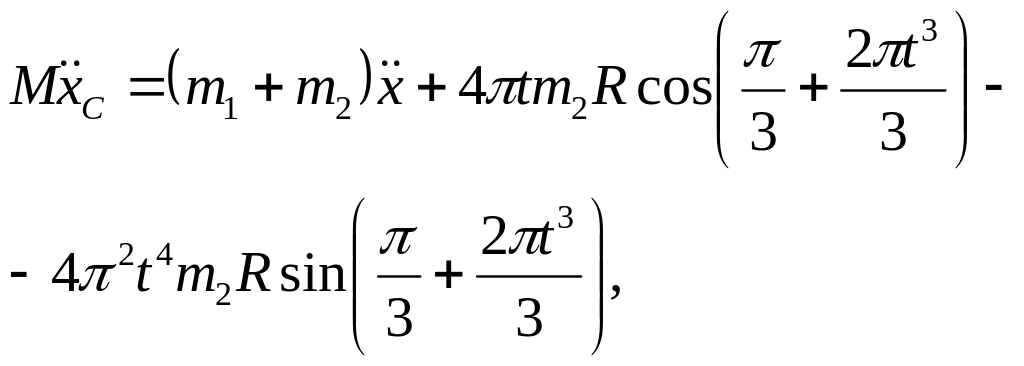
де - прискорення плити.

Згідно з рівнянням (1), . Тоді

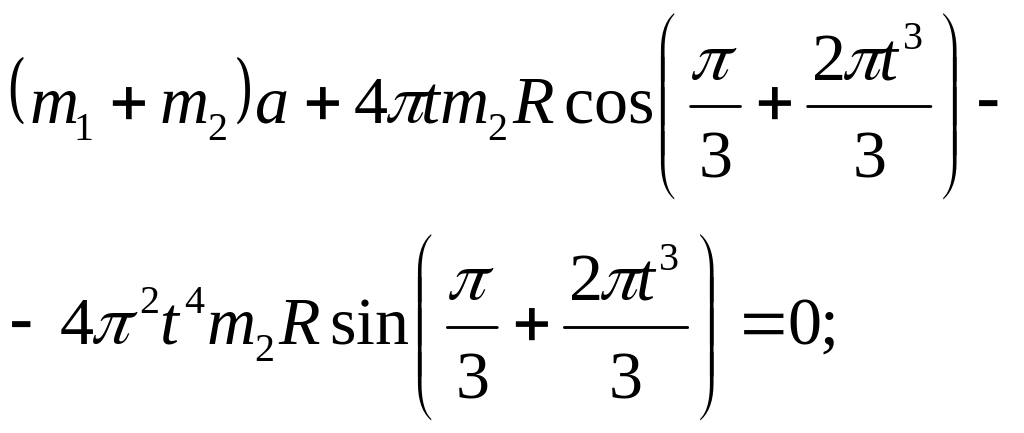
При t₁=1 c

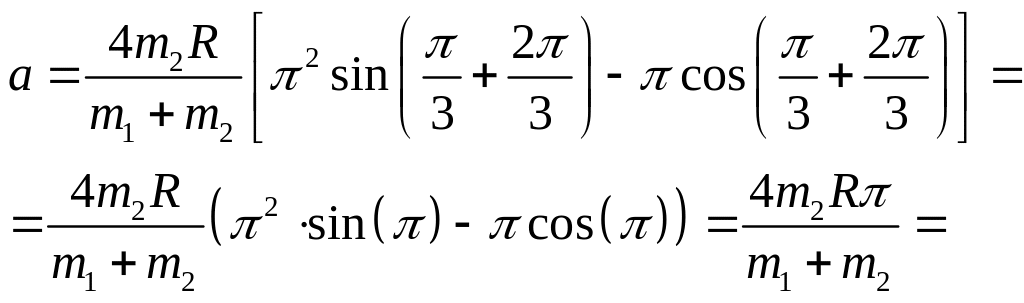
м/с².

Відповідь: a₁ =1,88 м/с². Знак показує, що прискорення плити направлене вправо.

3. За тих же умов задачі знайдемо —швидкість плити при t₁=1 c.

Розглянемо рух механічної системи в довільному положенні, прикладемо до тіл системи всі діючі зовнішні сили (рис. 21.13).

Для визначення u₁ використаємо теорему про зміну кількості руху механічної системи в проекції на вісь Ox в диференціальній формі

. (1)

Оскільки всі зовнішні сили, що діють на систему,-вертикальні, то

і або (2)

Для даної механічної системи, що складається з плити та тягаря D, буде

. (3)

Тут - кількість руху плити ( - швидкість плити);

- кількість руху тягаря D ( - абсолютна швидкість тягаря в його складному русі відносно осей координат Oxy).

Вважаючи рух тягаря D разом з плитою переносним, а його рух по відношенню до плити (по колу радіуса R)—відносним рухом, одержимо

;

. (4)

Але , значить . Вектор перпендикулярний до радіуса жолоба в точці D (проходить по дотичній до кола в точці D), а чисельно

(5)

Тоді

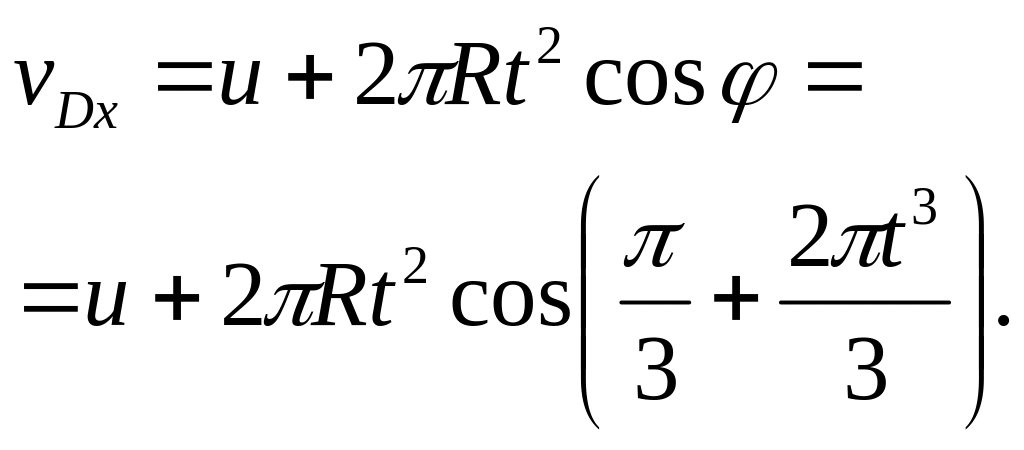(6)

З урахуванням рівностей (3) і (6) рівняння (2) приймає вигляд

(7)

При t₀=0 u=u₀=3 м/с і

(8)

Одержимо

звідки

(9)

При t₁=1 c

м/с.

Відповідь: м/с.

Примітка. Якщо жолоб, в якому рухається тягар D,-прямолінійний, то відносна швидкість і направлена по жолобу з урахуванням одержаного знака.

4. За тих же умов знайдемо значення повної реакції направляючих при t₁=1 c. Для цього скористаємось теоремою про рух центра мас системи в проекції на вісь Oy (див. рис. 21.13):

;

(1)

Звідси

. (2)

З формули, яка визначає ординату y_C центра мас системи одержимо

(3)

тут y—ордината центра ваги плити, y_D—ордината тягаря D.

З рисунка 21.13 визначимо, що

;

.

Тоді

(4)

Візьмемо від рівняння (4) дві похідні за часом:

Оскільки то і

(5)

(6)

Тоді

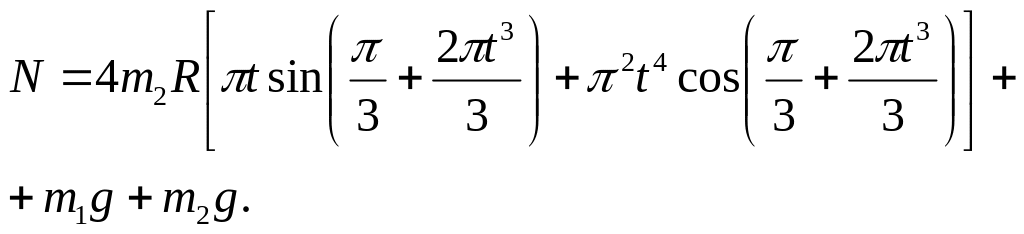(7)

При t₁ =1 c

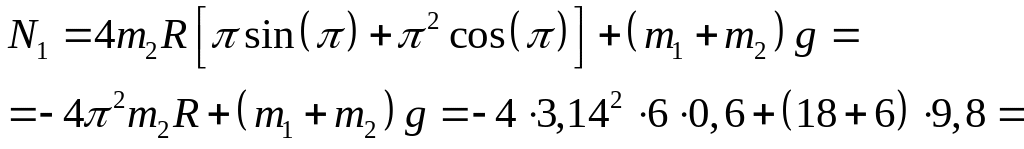
Н.

Відповідь: N₁=93,22 Н.