Преобразование Фурье

Преобразование Фурье (Fourier transform) является инструментом спектрального анализа непериодических сигналов. Впрочем, чуть позже мы увидим, что его можно применять и к сигналам периодическим, но это потребует использования аппарата обобщенных функций.

При спектральном анализе непериодических сигналов формула для расчета коэффициентов комплексного ряда Фурье модифицируется следующим образом:

• частота перестает быть дискретно меняющейся и становится непрерывным параметром преобразования (то есть kω₁ в формуле (1.9) заменяется на ω);

• удаляется множитель 1/T;

• результатом вычислений вместо нумерованных коэффициентов ряда C_k является функция частоты S(ω) - спектральная функция сигнала s(t). Иногда ее называют также спектральной плотностью.

В результате перечисленных модификаций формула (1.9) превращается в формулу прямого преобразования Фурье:

(1.11)

В формуле самого ряда Фурье суммирование, естественно, заменяется интегрированием (и, кроме того, перед интегралом появляется деление на 2π). Получающееся выражение называется обратным преобразованием Фурье:

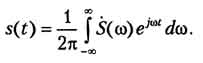
Если анализируемый сигнал s(t) - вещественная функция, то соответствующая спектральная функция S^·(ω) является "сопряженно-симметричной" относительно нулевой частоты. Это означает, что значения спектральной функции на частотах ω и - ω являются комплексно-сопряженными по отношению друг к другу:

Если s(t) - четная функция, то, как и в случае ряда Фурье, спектр будет чисто вещественным (и, следовательно, будет являться четной функцией). Если, напротив, s(t) - функция нечетная, то спектральная функция S^·(ω) будет чисто мнимой (и нечетной).

Модуль спектральной функции часто называют амплитудным спектром, а ее аргумент - фазовым спектром.

Прямоугольный импульс

Начнем с прямоугольного импульса, центрированного относительно начала отсчета времени (рис. 1.10):

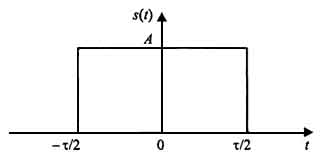Рис. 1.10. Прямоугольный импульс

Вычисляем спектральную функцию:

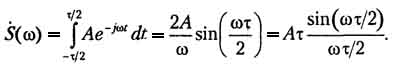
Как видите, спектр представляет собой функцию вида sin(x)/x (рис. 1.11). Амплитудный спектр имеет лепестковый характер, и ширина лепестков равна 2π/τ, то есть обратно пропорциональна длительности импульса. Значение спектральной функции на нулевой частоте равно площади импульса - Aτ. Спектральная функция является вещественной, поэтому фазовый спектр принимает лишь два значения - 0 и π, в зависимости от знака функции sin(x)/x. Значения фазы π и - π неразличимы, разные знаки для фазового спектра при ω > 0 и ω < 0 использованы лишь с целью представить его в виде нечетной функции.

Рис. 1.11. Амплитудный (слева) и фазовый (справа) спектры прямоугольного импульса

Несимметричный треугольный импульс

Далее рассмотрим несимметричный треугольный импульс (рис. 1.14):

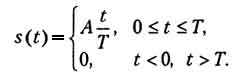
Рис. 1.14. Несимметричный треугольный импульс

Рассчитываем спектр и строим графики (рис. 1.15):

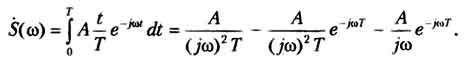
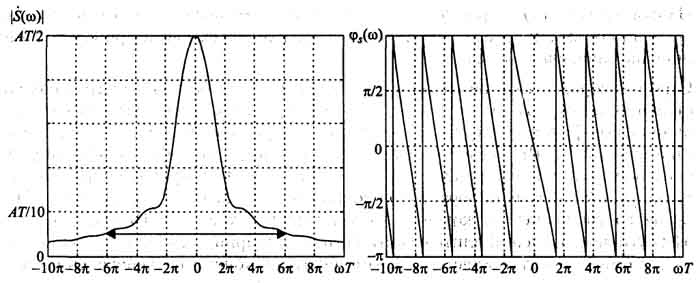Рис. 1.15. Амплитудный (слева) и фазовый (справа) спектры несимметричного треугольного импульса

На сей раз амплитудный спектр не содержит ярко выраженных лепестков, поэтому для определения его эффективной ширины необходим иной критерий; Будем определять эффективную ширину спектра по уровню 0,1 от максимума. Из графика видно, что эта ширина (она показана стрелкой) составляет примерно 6π/T. База сигнала, таким образом, равна 6π.

Симметричный треугольный импульс

Следующий сигнал - симметричный треугольный импульс (рис. 1.16):

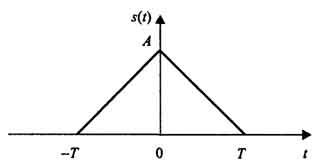Рис. 1.16. Симметричный треугольный импульс

Рассчитываем спектральную функцию:

Далее строим график амплитудного спектра (рис. 1.17). Спектральная функция оказывается не только вещественной (это сразу же следует из четности сигнала), но и неотрицательной, поэтому фазовый спектр в данном случае чисто нулевой и строить его график не имеет смысла.

Рис. 1.17. Амплитудный спектр симметричного треугольного импульса

Из графика видно, что спектр опять имеет лепестковую структуру и ширина главного лепестка составляет 2π/T, как и в случае прямоугольного импульса. Однако длительность сигнала в данном случае вдвое больше (2T), и база оказывается равной 4π.

Односторонний экспоненциальный импульс

Первым из сигналов бесконечной длительности будет рассмотрен односторонний экспоненциальный импульс (рис. 1.18):

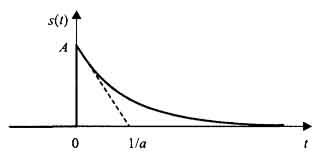Рис. 1.18. Односторонний экспоненциальный импульс

Рассчитываем преобразование Фурье:

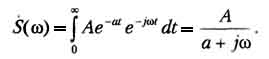
Далее строим графики амплитудного и фазового спектров (рис. 1.19).

Рис. 1.19. Амплитудный (слева) и фазовый (справа) спектры одностороннего экспоненциального импульса

Гауссов импульс

Следующий очень важный сигнал - гауссов импульс (рис. 1.22). Как и предыдущий, он имеет бесконечную протяженность в обоих направлениях временной оси:

s(t) = Ae^{- a^2t^2}.

Рис. 1.22. Гауссов импульс

Вычисляем спектр:

Поскольку сигнал является четной функцией, его спектр чисто вещественный. Поэтому строим график только для амплитудного спектра (рис. 1.23).

Важным свойством гауссова импульса является то, что его спектр тоже описывается гауссовой функцией.

Гауссов импульс имеет бесконечную протяженность как во временной, так и в частотной области. Определим его эффективную длительность и ширину спектра по уровню 1/e от максимума: τ = 2/a, ∆ω = 2a. База сигнала, таким образом, равна четырем.

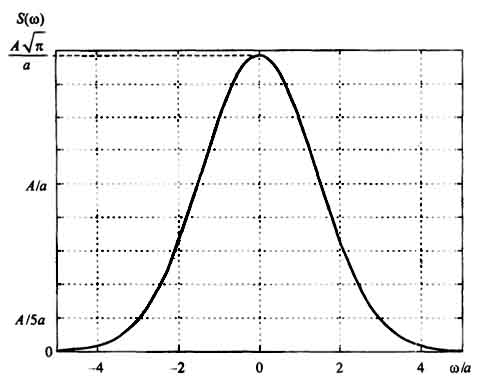Рис. 1.23. Амплитудный спектр гауссова импульса

Сигнал вида sin(x)/x

Следующий пример призван продемонстрировать дуальность преобразования Фурье. Если сравнить формулы прямого и обратного преобразования Фурье, можно заметить, что они отличаются друг от друга лишь знаком в показателе комплексной экспоненты и множителем перед интегралом. Отсюда следует, что если четной функции времени f(t) соответствует спектральная функция g(ω) (она будет также четной), то функции времени g(t) будет соответствовать спектральная функция 2πf(ω). Проверим это на конкретном примере. В начале этого раздела мы выяснили, что прямоугольному импульсу соответствует спектральная функция вида sin(ω)/ω. Теперь же рассмотрим временной сигнал вида sin(t)/t и проверим, будет ли его спектральная функция прямоугольной.

Итак, задаем временной сигнал (используем параметр T для обозначения полупериода функции sin) (рис. 1.24):

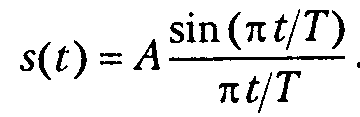
Рассчитываем спектр и строим график (рис. 1.25):

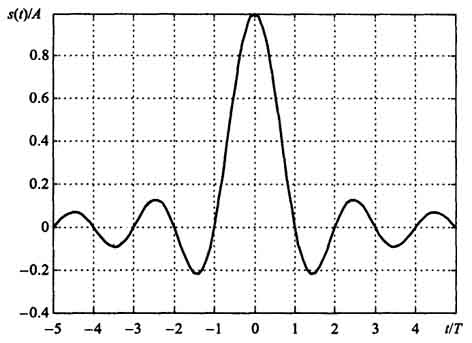Рис. 1.24. Сигнал вида sin(at)/(at)

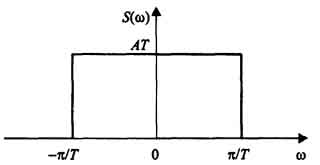Рис. 1.25. Сигнал вида sin(at)/(at) имеет прямоугольный спектр

Значение каждого из двух получившихся интегралов равно ± π в зависимости от знака множителей (ω ± π/T). Поэтому результат суммирования интегралов зависит от частоты следующим образом:

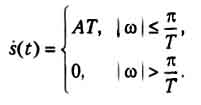
Как видите, дуальность (симметрия) преобразования Фурье получила наглядное подтверждение.

Сигнал данного вида имеет идеальный низкочастотный спектр - спектральная функция постоянна в некоторой полосе частот, начинающейся от нулевой частоты, и равна нулю за пределами этой полосы.

Дельта-функция

Дельта-функция δ(t), или функция Дирака, представляет собой бесконечно узкий импульс с бесконечной амплитудой, расположенный при нулевом значении аргумента функции. "Площадь" импульса тем не менее равна единице:

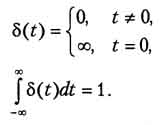
Разумеется, сигнал в виде дельта-функции невозможно реализовать физически, однако эта функция очень важна для теоретического анализа сигналов и систем.

Прежде всего вычислим преобразование Фурье для сигнала в виде дельта-функции:

Спектр дельта-функции представляет собой константу, то есть является равномерным в бесконечной полосе частот. Это вполне согласуется с общим соотношением между длительностью сигнала и шириной его спектра: дельта-импульс имеет бесконечно малую длительность, а его спектр бесконечно широк.

Гармонический сигнал

Рассчитаем спектр гармонического сигнала общего вида:

s(t) = A cos(ω₀t + φ).

Для расчета спектральной функции представим косинус в виде полусуммы комплексных экспонент и воспользуемся формулой (1.19):

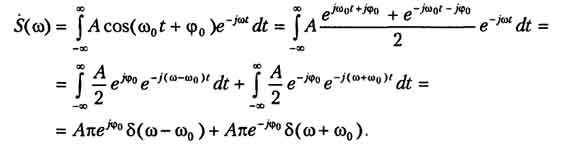
(1.20)

Результат, как видим, представляет собой пару дельта-функций, расположенных на частотах ± ω₀. Множители при них отражают амплитуду и начальную фазу (то есть комплексную амплитуду ) гармонического сигнала.