
МОДУЛЬ № 3
ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ. ЛИНИИ НА ПЛОСКОСТИ. ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ.
ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ.
Векторы на плоскости и в пространстве.
Основные понятия.
Линейные операции над векторами.
Проекция вектора на ось.
Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы вектора.
Скалярное произведение векторов и его свойства.
Определение скалярного произведения.
Свойства скалярного произведения.
Выражение скалярного произведения через координаты.
ЗАДАЧИ И УПРАЖНЕНИЯ по теме: «Элементы векторной алгебры»
1. Найти
координаты вектора
![]() ,
если А(-1; 2; -4); В(2;-4;-1).
,
если А(-1; 2; -4); В(2;-4;-1).
2. Найти
длину вектора
![]() ,
если
,
если
![]() ;
;
![]() .
.
3.
![]() .
Найти у.
.
Найти у.
4.
![]() .
Найти координаты вектора
.
Найти координаты вектора
![]() ,
если координаты вектора
,
если координаты вектора
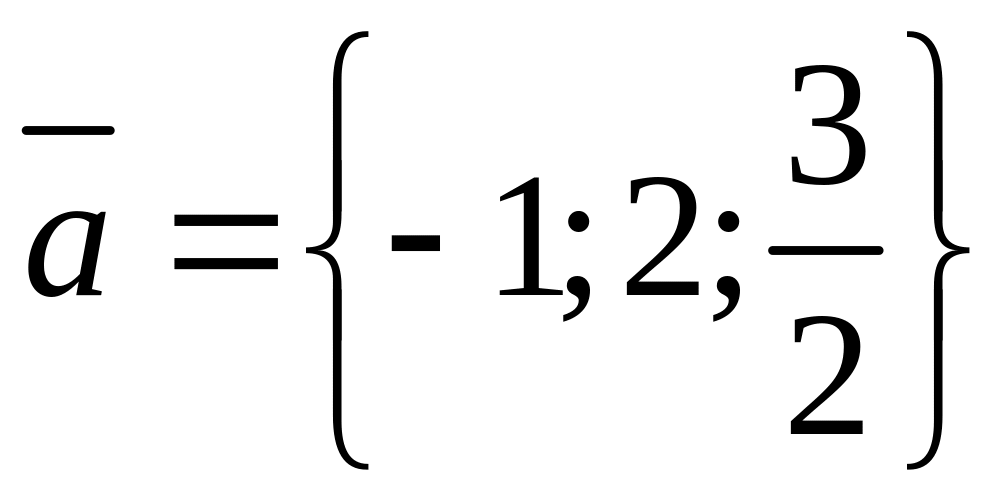 .
.
5.
При каких
![]() и
и
![]() векторы
векторы
![]() коллинеарны?
коллинеарны?
6.
Коллинеарны ли векторы
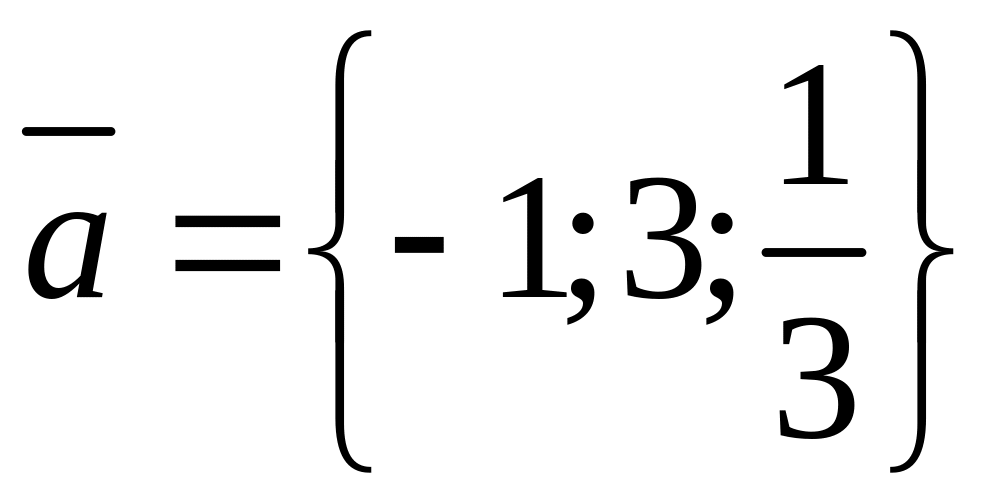 и
и
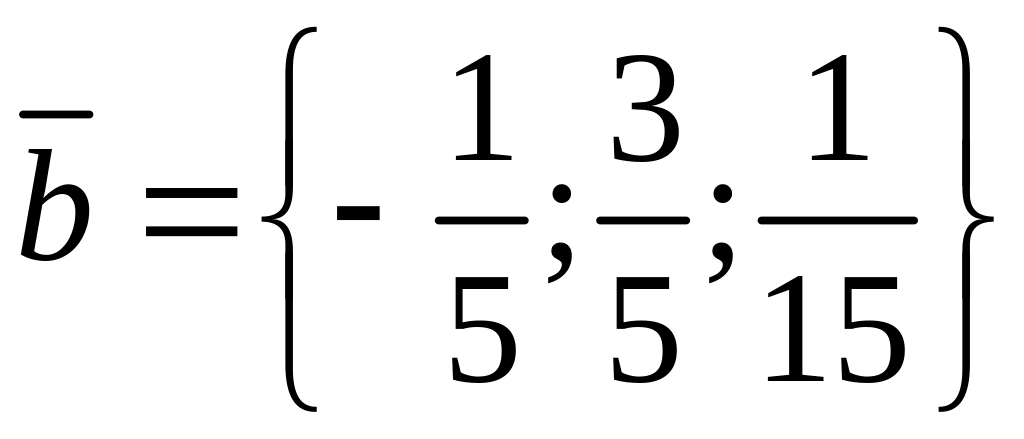 ?
Если коллинеарны, то какой из них длиннее
и во сколько раз? Как они направлены: в
одну или противоположные стороны?
?
Если коллинеарны, то какой из них длиннее
и во сколько раз? Как они направлены: в
одну или противоположные стороны?
7.
Найти орт вектора
![]() .
.
8.
Вычислить координаты вектора
![]() ,
если
,
если
![]() ;
углы, которые этот вектор составляет с
осями координат Ох; Оу; Оz
равны соответственно
;
углы, которые этот вектор составляет с
осями координат Ох; Оу; Оz
равны соответственно
![]()
9.
Вектор
![]() составляет с осями координат Оу и Оz
углы
составляет с осями координат Оу и Оz
углы
![]() Какой угол этот вектор составляет с
осью Ох?
Какой угол этот вектор составляет с
осью Ох?
10.
![]() ;
;
![]() ;
;
![]() .
Найти координату х
.
Найти координату х
вектора .
11. Найти
направляющие косинусы вектора
![]() ,
если
,
если
![]() .
.
12. Найти
координаты вектора
![]() в
базисе
в
базисе
![]() .
.
13. Разложить
вектор
![]() по векторам
по векторам
![]() .
.
14.
![]() .
Угол между векторами
и
равен
.
Угол между векторами
и
равен
![]() .
Найти скалярное произведение векторов
.
Найти скалярное произведение векторов
![]() .
.
15.
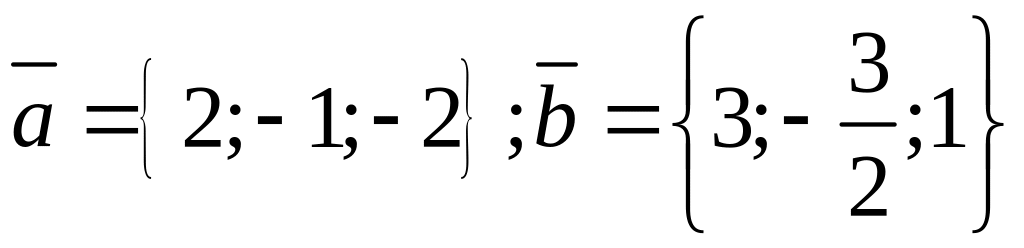 .
Найти
.
Найти
![]() .
.
16. При
каком
векторы
![]() ;
;
![]() взаимно перпендикулярны?
взаимно перпендикулярны?
17. Найти
угол между векторами
![]() ;
;
![]() .
.
18. Даны
вершины треугольника
![]() .
Определить его внутренний угол при
вершине С.
.
Определить его внутренний угол при
вершине С.
19. Есть
ли среди векторов
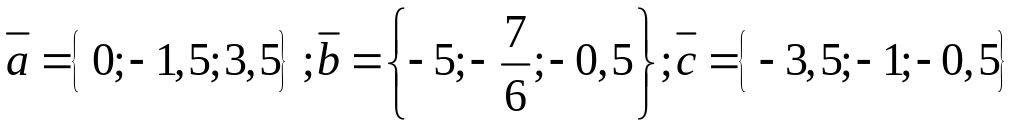 пары взаимно перпендикулярных? Ответ
обосновать.
пары взаимно перпендикулярных? Ответ
обосновать.
20. Найти
координаты вектора
![]() зная, что он перпендикулярен векторам
зная, что он перпендикулярен векторам
![]() и
и
![]() ,
и удовлетворяет условию
,
и удовлетворяет условию
![]() .
.
ОТВЕТЫ к задачам темы «Элементы векторной алгебры»:
1. Ответ:
![]() ;
2. Ответ:
;
2. Ответ:![]() ;
3. Ответ:
;
3. Ответ:
![]() ;
4. Так
как
;
4. Так
как
![]() то
то
 ;
5. 6;
1,5; 6.
;
5. 6;
1,5; 6.
![]() ;
7.
;
7.
![]() ;
;
8.
![]() ;
9.
;
9.
![]() или
;
10. 4;
11.
или
;
10. 4;
11.
![]() ;
12.
;
12.
![]() ;
13.
;
13.
![]() ;
14. 9;
15.
;
14. 9;
15.
![]() ;
16. 5;
;
16. 5;
17.
![]() ;
18.
;
18.
![]() ;
19.
;
19.
![]() ,
так как
,
так как
![]() ;
20.
;
20.
![]() .
.
ЛИНИИ НА ПЛОСКОСТИ
Прямая линия на плоскости.
Линии второго порядка на плоскости: окружность; эллипс; гипербола; парабола.
ЗАДАЧИ И УПРАЖНЕНИЯ по теме: «Линии на плоскости»
1. Принадлежит
ли точка
![]() прямой
прямой
![]() ?
?
2. Точка
![]() принадлежит
прямой
принадлежит
прямой
![]() .Найти
у.
.Найти
у.
3. Прямая
задана уравнением
![]() .
Написать уравнение этой прямой
.
Написать уравнение этой прямой
а) с угловым коэффициентом;
б) в отрезках на осях.
4. Задана
прямая
![]() .
Указать:
.
Указать:
а) один из векторов нормали этой прямой;
б) один из направляющих векторов этой прямой.
5. Составить
уравнение прямой, проходящей через
точку
![]() перпендикулярно
вектору
перпендикулярно
вектору
![]() .
.
6. Написать
уравнение прямой, проходящей через
точку А перпендикулярно вектору
,
если![]() .
.
7.
Составить уравнение прямой, проходящей
через точку
![]() параллельно
вектору
параллельно
вектору
![]() .
.
8. Прямая
задана уравнением
![]() .
Составить уравнение прямой, проходящей
через точку
.
Составить уравнение прямой, проходящей
через точку
![]()
а) параллельно данной прямой;
б) перпендикулярно данной прямой.
9. Составить
уравнение прямой, проходящей через
точки
![]() .
.
10. Заданы
уравнения двух прямых
![]() ;
при каких значениях
эти прямые
;
при каких значениях
эти прямые
а) параллельны?
б) перпендикулярны?
11. Заданы
вершины треугольника АВС:
![]() .
Составить уравнение стороны АВ и медианы
ВМ.
.
Составить уравнение стороны АВ и медианы
ВМ.
12. Найти
угол между прямыми
![]() .
.
13. Найти
расстояние от точки
![]() до прямой
до прямой
![]() .
.
14. Составить
уравнение окружности, проходящей через
начало координат, если центр окружности
находится в точке![]() .
Построить эту окружность.
.
Построить эту окружность.
15. На
кривой
 найти точки, ордината которых равна
найти точки, ордината которых равна
![]() .
Построить кривую и найденные точки.
.
Построить кривую и найденные точки.
16. Вычислить
площадь треугольника, образованного
асимптотами гиперболы
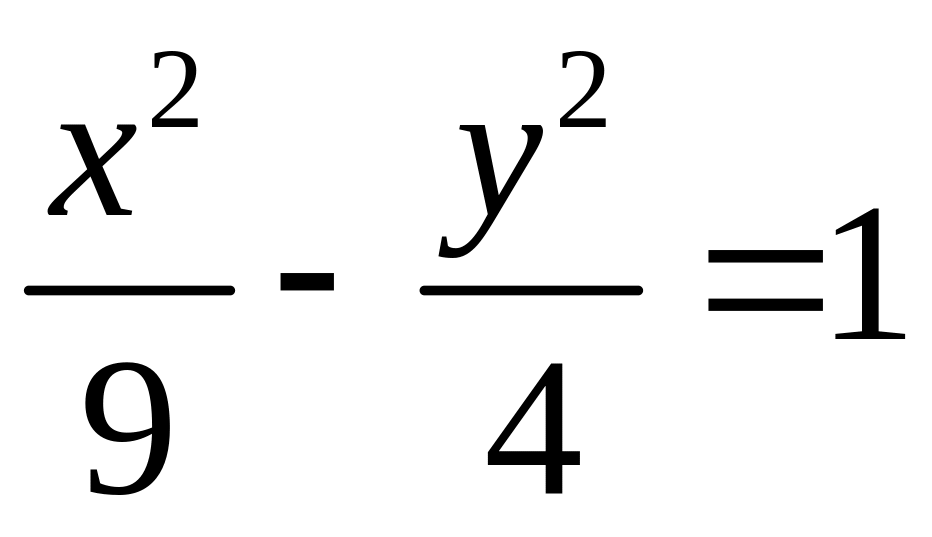 и прямой х
= 1. Сделать чертеж.
и прямой х
= 1. Сделать чертеж.
17. Построить линии, заданные уравнениями:
17.1.
![]() ;
17.2.
;
17.2.
![]() ;
;
17.3.
![]() ;
17.4.
;
17.4.
![]() ;
;
17.5.
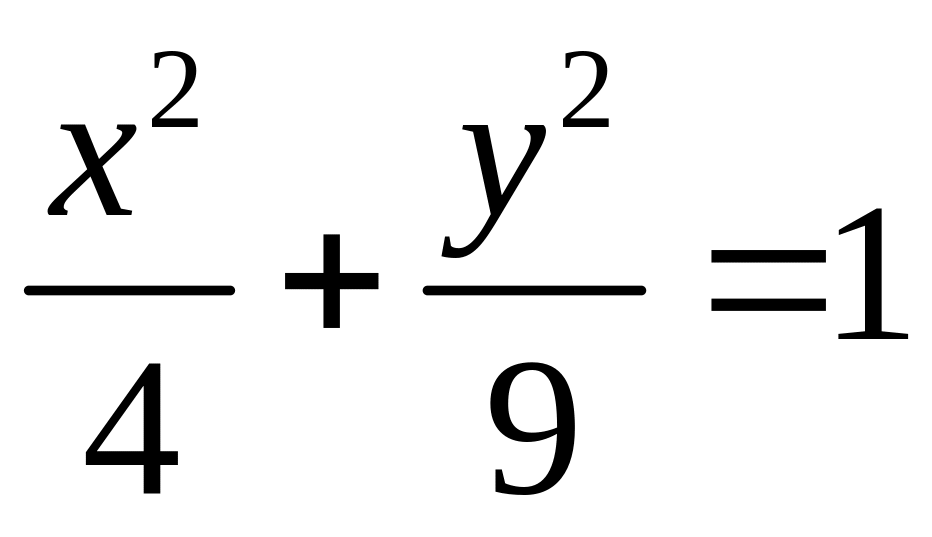 ;
17.6.
;
17.6.
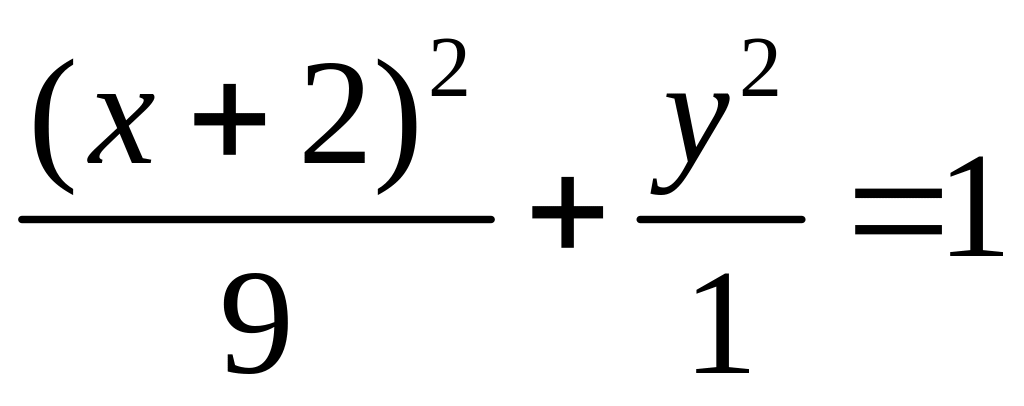 ;
;
17.7.
![]() ;
17.8.
;
17.8.
![]() ;
;
17.9.
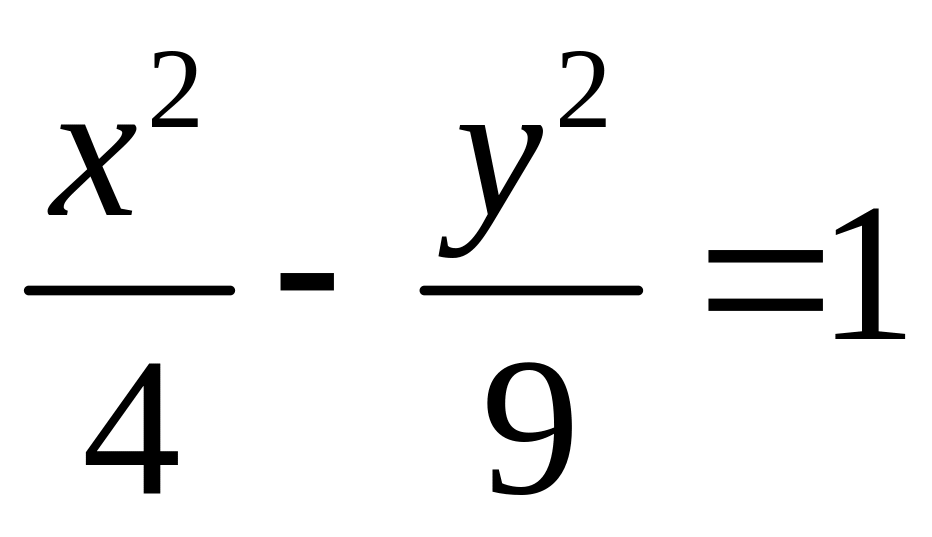 ;
17.10.
;
17.10.
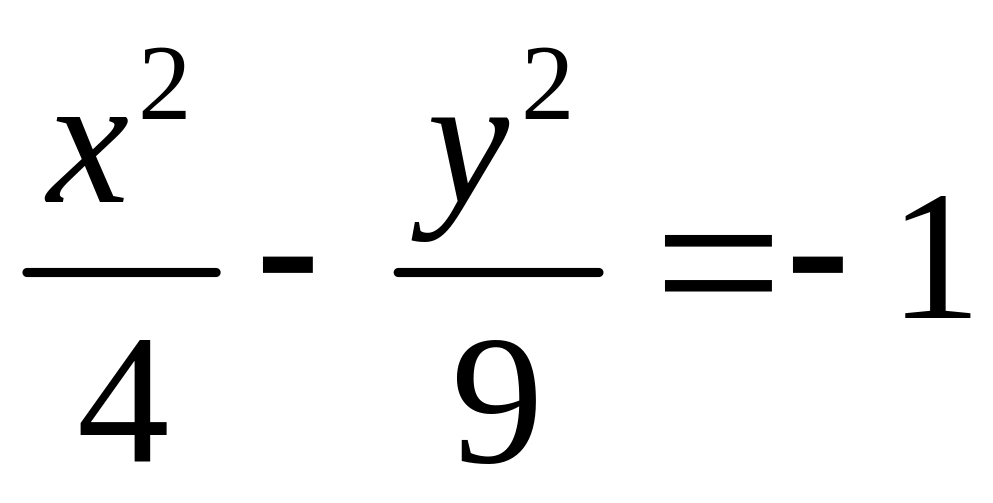 ;
;
17.11.
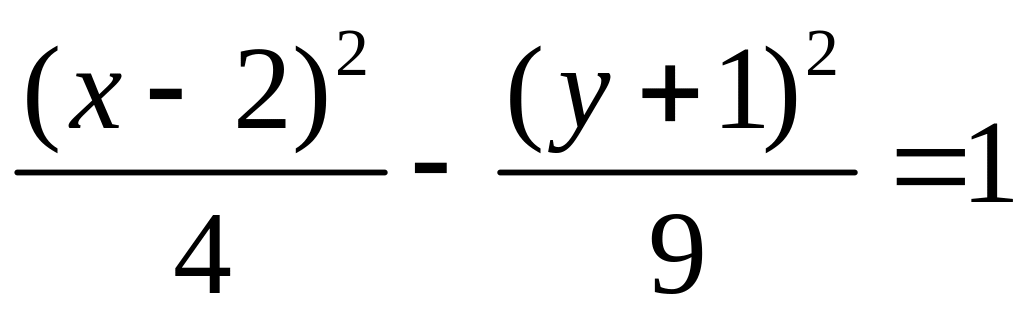 ;
17.12.
;
17.12.
![]() ;
;
17.13.
![]() ;
17.14.
;
17.14.
![]() ;
;
17.15.
![]() .
.
ОТВЕТЫ к задачам темы «Линии на плоскости».
1. Нет,
не принадлежит; 2.
![]() ;
3. а)
;
3. а)
![]() ;
б)
;
б)
![]() ;
;
4. а)![]() ;
б)
;
б)
![]() ;
5.
;
5.
![]() ;
6.
;
6.
![]() ;
;
7.
![]() ;
8. а)
;
8. а)
![]() ;
б)
;
б)
![]() ;
9.
;
9.
![]() ;
;
10. а)
![]() ;
б)
;
б)
![]() ;
11.
;
11.
![]() ;
;
![]() ;
12.
;
12.
![]() ;
;
13.
![]() ;
14.
;
14.
![]() .
15.
.
15.
 ;16.
;16.
![]() .
.
УРАВНЕНИЯ ПОВЕРХНОСТИ И ЛИНИИ В ПРОСТРАНСТВЕ
Уравнения плоскости в пространстве.
Уравнения прямой в пространстве.
Прямая и плоскость в пространстве.
Канонические уравнения поверхностей второго порядка
ЗАДАЧИ И УПРАЖНЕНИЯ по теме: «Поверхности и линии в пространстве»
1. Составить
уравнение плоскости, проходящей через
точку
![]() перпендикулярно вектору
перпендикулярно вектору
![]() .
.
2. Найти
координаты точек пересечения плоскости
![]() с осями координат.
с осями координат.
3. Найти
направляющие косинусы вектора нормали
плоскости
![]() .
.
4. При
каких значениях параметров а
и
![]() уравнения
уравнения
![]() и
и
![]() определяют параллельные плоскости?
определяют параллельные плоскости?
5. При
каком значении параметра а
уравнения
![]() и
и
![]() определяют перпендикулярные плоскости?
определяют перпендикулярные плоскости?
6. Найти
расстояние от точки
![]() до плоскости
до плоскости
![]() .
.
7. Составить
канонические уравнения прямой, проходящей
через точку
![]() перпендикулярно плоскости
перпендикулярно плоскости
![]() .
.
8. Составить
канонические уравнения прямой, проходящей
через точки
![]() и
и
![]() .
.
9. Составить
канонические уравнения прямой, проходящей
через точку
![]() параллельно
параллельно
а) прямой
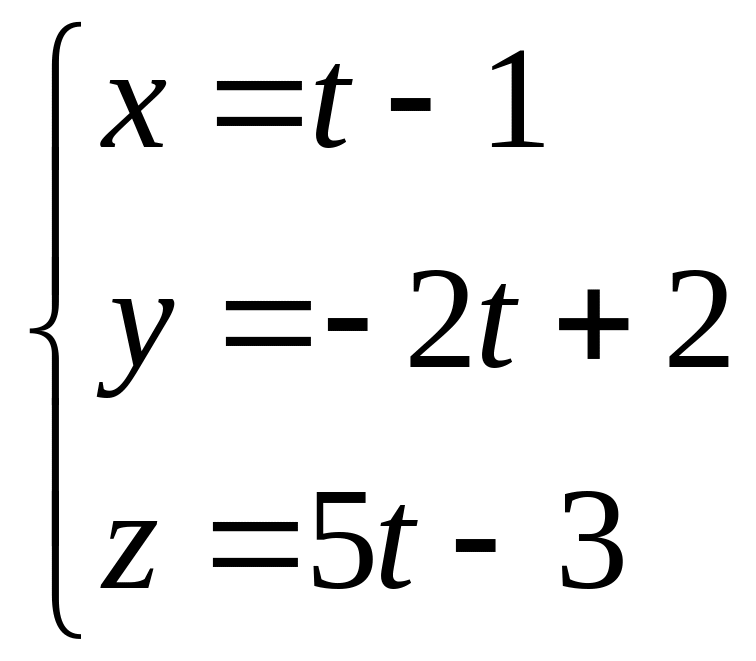 ;
;
б) оси
![]() .
.
10. Найти
точку пересечения прямой
![]() и плоскости
и плоскости
![]() .
.
11. Прямая
задана как линия пересечения двух
плоскостей
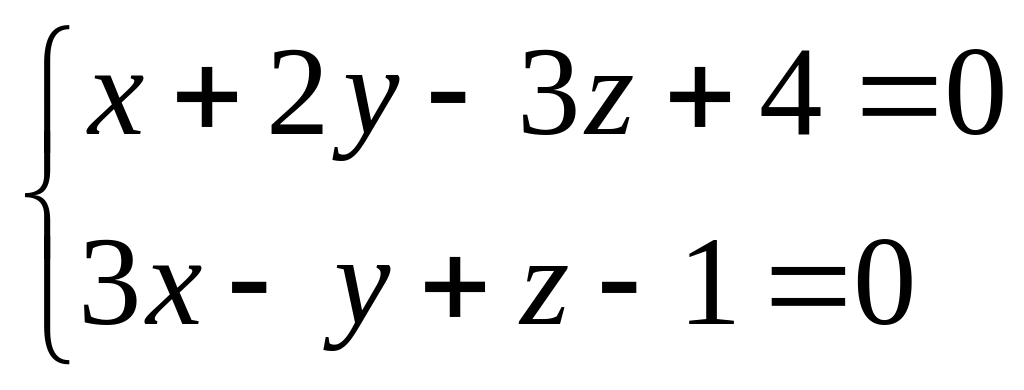 .
Написать ее канонические и параметрические
уравнения.
.
Написать ее канонические и параметрические
уравнения.
12. Составить
канонические уравнения прямой, проходящей
через точку
![]() параллельно прямой
параллельно прямой
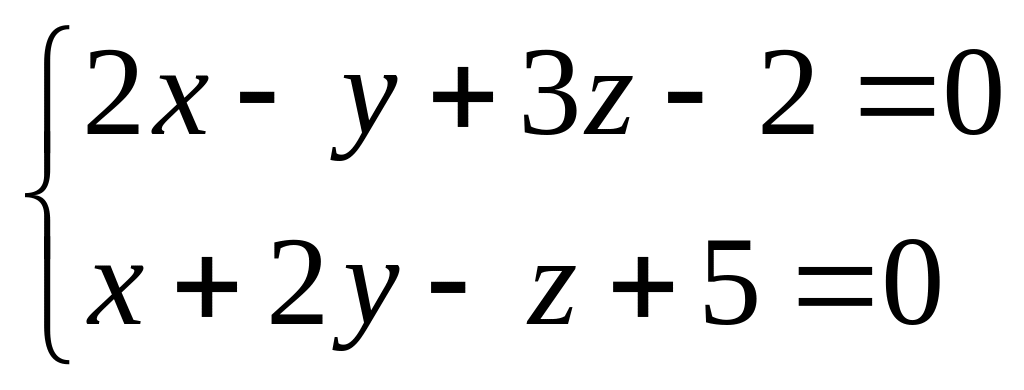 .
.
13. Доказать перпендикулярность прямых
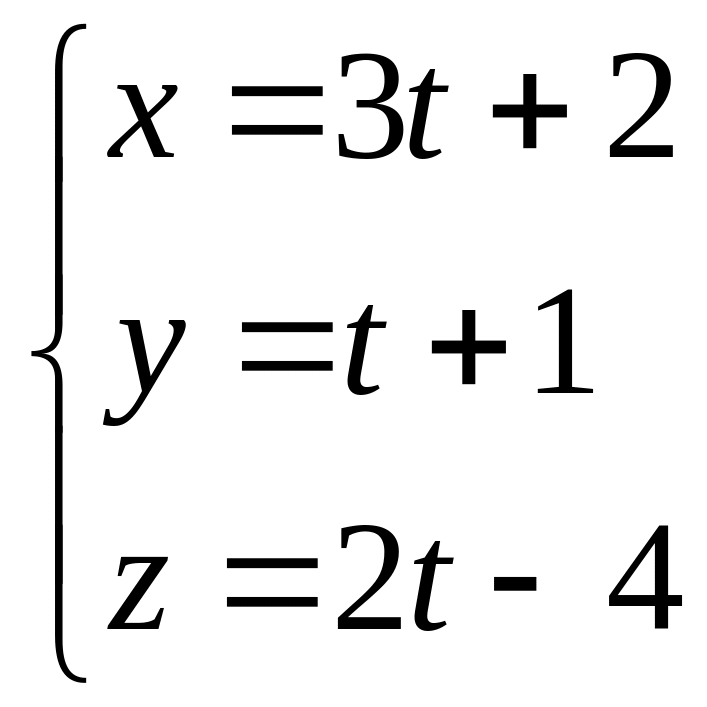 и
.
и
.
14. Найти
проекцию точки
![]() на плоскость, заданную уравнением
.
на плоскость, заданную уравнением
.
15. Найти
проекцию точки
![]() на прямую, заданную уравнением
на прямую, заданную уравнением
![]() .
.
16. Найти точку, симметричную точке относительно прямой .
17. Найти точку, симметричную точке относительно плоскости .
18. Найти
угол между прямой
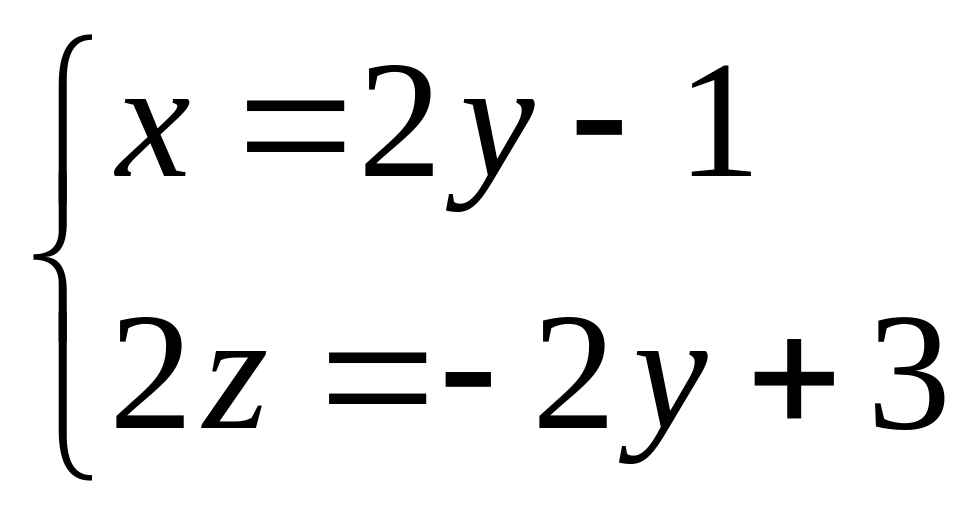 и
и
плоскостью
![]() .
.
19. Составить
уравнение плоскости, проходящей через
ось
параллельно вектору
![]() .
.
20. Построить
на плоскости
![]() проекцию линии пересечения плоскости
проекцию линии пересечения плоскости
![]() и поверхности
и поверхности
![]() ,
если:
,
если:
20.1.
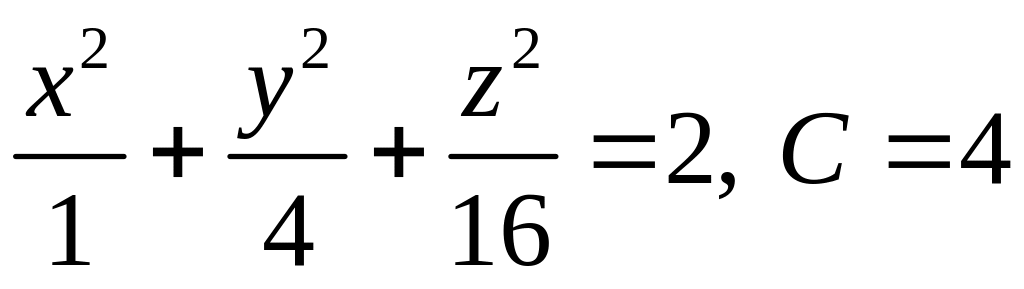 ;
;
20.2.
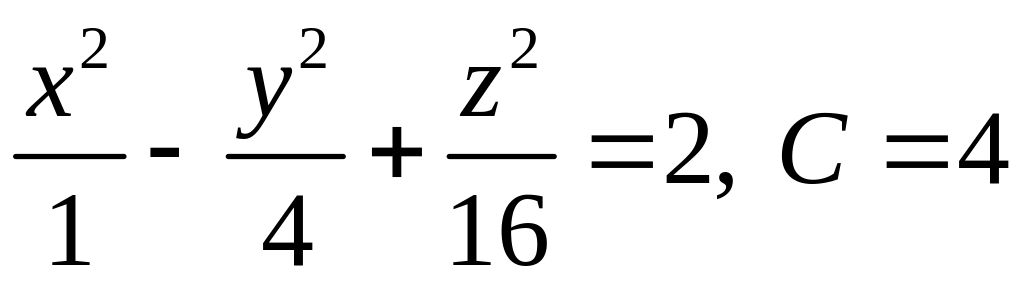 ;
;
20.3.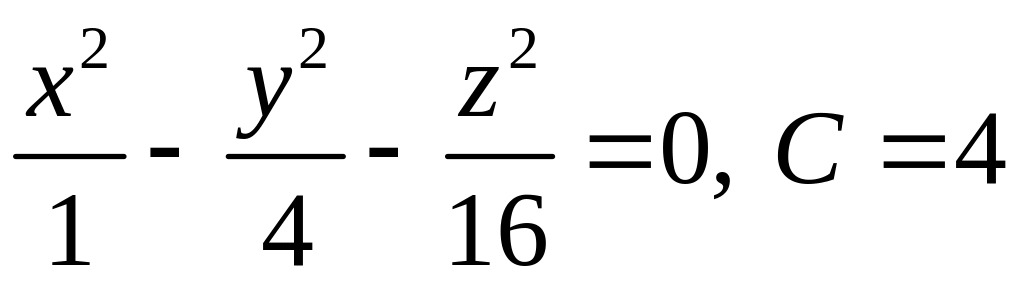 .
.
ОТВЕТЫ к задачам темы «Поверхности и линии в пространстве».
1.
![]() ;
2.
;
2.
![]() ;
3.
;
3.
![]() ;
;
4.
![]() ;
5.
;
5.
![]() ;
6.
;
6.
![]() ;
7.
;
7.
![]() ;
;
8.
![]() ;
9. а)
;
9. а)
![]() ;
б)
;
б)
![]() ;
;
10.
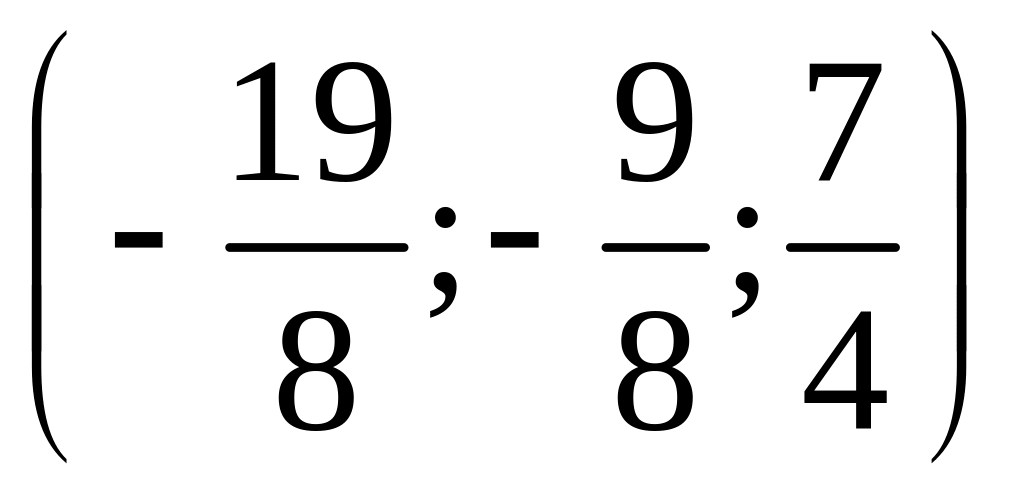 ;
11.
;
11.
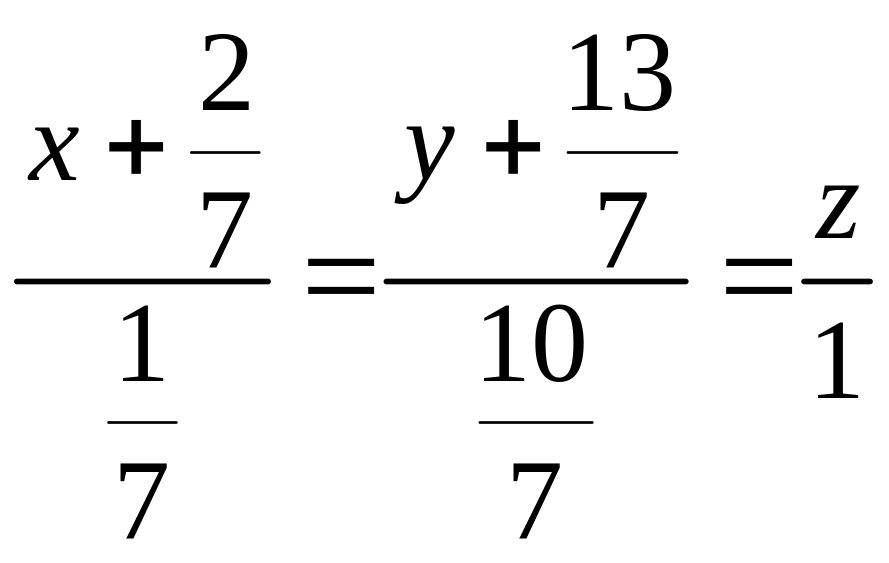 ;
;
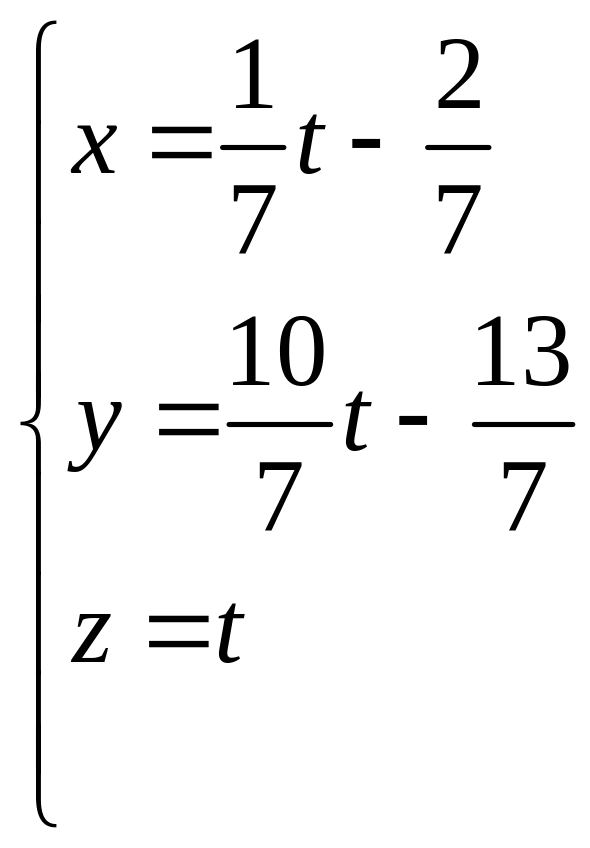 ;
;
12.
![]() ;
14.
;
14.
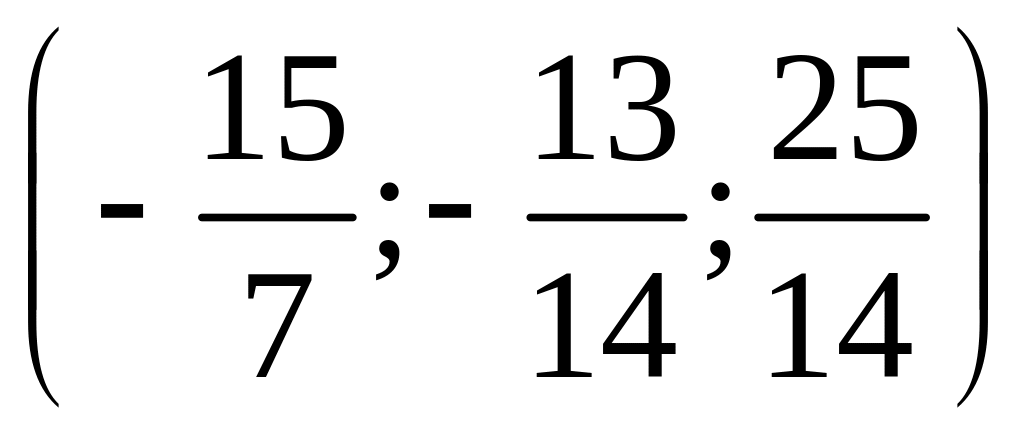 ;
15.
;
15.
![]() ;
;
16.
![]() ;
17.
;
17.
 ;
18.
;
18.
 ;
19.
;
19.
![]() .
.
КОНТРОЛЬНОЕ ЗАДАНИЕ по темам: «Элементы векторной алгебры. Линии на плоскости. Поверхности и линии в пространстве».
1. Найти
координаты вектора
![]() ,
если
,
если
![]() .
.
2. Найти длину вектора , если .
3.
![]()
Найти координаты
вектора
,
если
![]() .
.
4. Коллинеарны
ли векторы
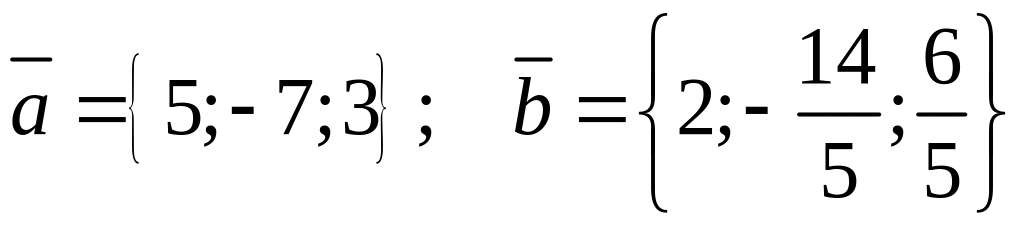 ?
Если коллинеарны, то какой из них длиннее
и во сколько раз, как они направлены: в
одну или противоположные стороны?
?
Если коллинеарны, то какой из них длиннее
и во сколько раз, как они направлены: в
одну или противоположные стороны?
5. При
каком
![]() векторы
векторы
![]() перпендикулярны?
перпендикулярны?
6. Найти угол между векторами .
7. Задана
прямая
![]() .
Указать:
.
Указать:
а) один из векторов нормали этой прямой;
б) один из направляющих векторов этой прямой.
8. Прямая
задана уравнением
![]() .
Составить уравнение прямой, проходящей
через точку А(-4; 1)
.
Составить уравнение прямой, проходящей
через точку А(-4; 1)
а) параллельно данной прямой;
б) перпендикулярно данной прямой.
9. Составить уравнение прямой, проходящей через точки А(-1; 3); В(2; -1).
10. Найти
угол между прямыми
![]() .
.
11. Найти
расстояние от точки М(-1; 5) до прямой
![]() .
.
12. При каких значениях параметров а и уравнения
![]() и
и
![]() определяют параллельные
определяют параллельные
плоскости?
13. При
каком значении параметра а
уравнения
![]() и
и
![]() определяют перпендикулярные плоскости?
определяют перпендикулярные плоскости?
14. Найти
расстояние от точки
![]() до плоскости
до плоскости
![]() .
.
15. Составить
канонические уравнения прямой, проходящей
через точку
![]() перпендикулярно плоскости
перпендикулярно плоскости
![]() .
.
16. Составить канонические уравнения прямой, проходящей через точку параллельно
а) прямой
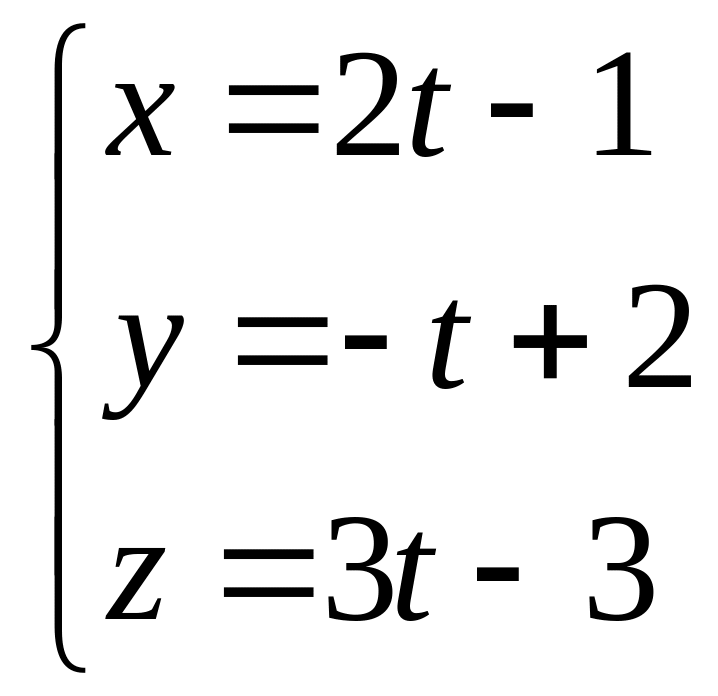 ;
;
б) оси
![]() .
.
17. Найти
точку пересечения прямой
![]() и
и
плоскости
![]() .
.
18. Прямая задана как линия пересечения двух плоскостей
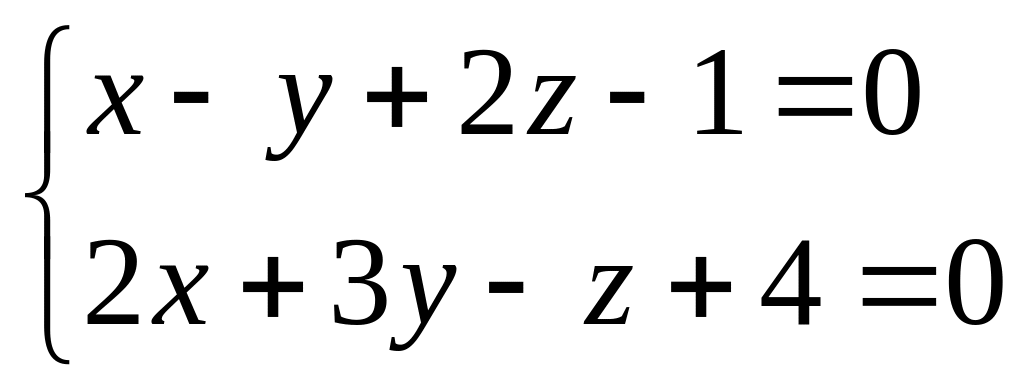 .
Написать ее канонические и
.
Написать ее канонические и
параметрические уравнения.
19. Найти
проекцию точки
![]() на плоскость, заданную
на плоскость, заданную
уравнением .
ОТВЕТЫ к контрольному заданию по темам: «Элементы векторной алгебры. Линии на плоскости. Поверхности и линии в пространстве».
1.
![]() ;
2.
;
2.
![]() ;
3.
;
3.
![]() ;
;
4.
![]() ;
5.
;
5.
![]() ;
6. Угол между
векторами равен
;
6. Угол между
векторами равен
![]() ;
7.
;
7.
![]() ;
8.
;
8.
![]() ;
;
9.
![]() ;
10.
;
10.
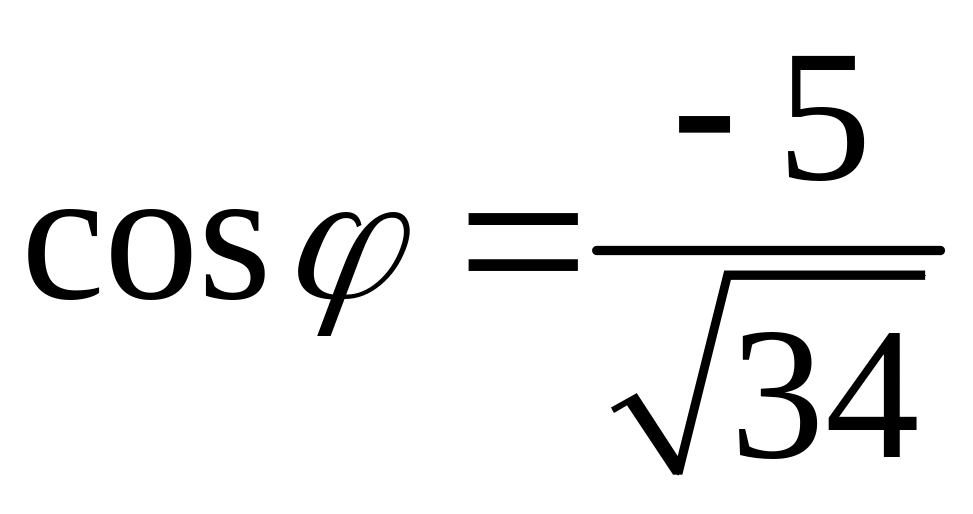 ;
11. 4; 12.
;
11. 4; 12.
![]() ;
;
13.
![]() ;
14.
;
14.
![]() ;
15.
;
15.
![]() ;
;
16.
![]() ;
17.
;
17.
![]() ;
;
18.
![]() ;
;
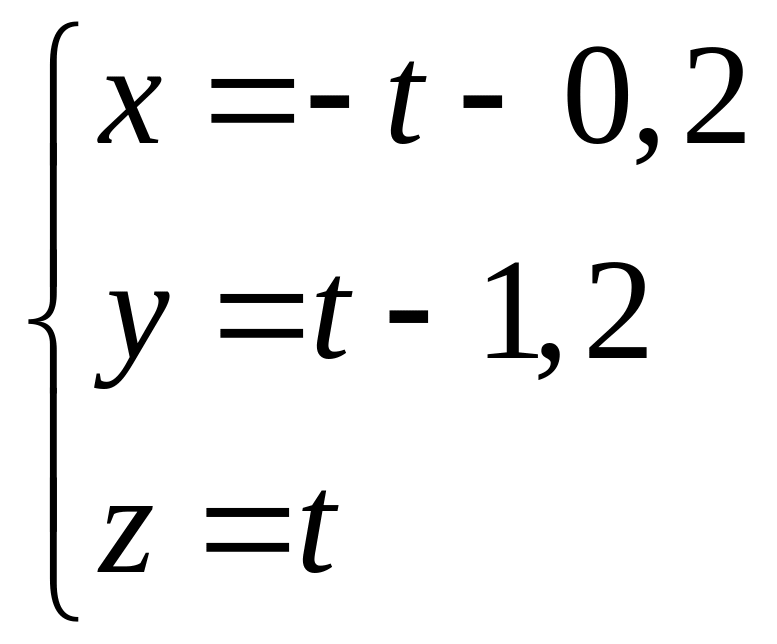 ;
19.
;
19.
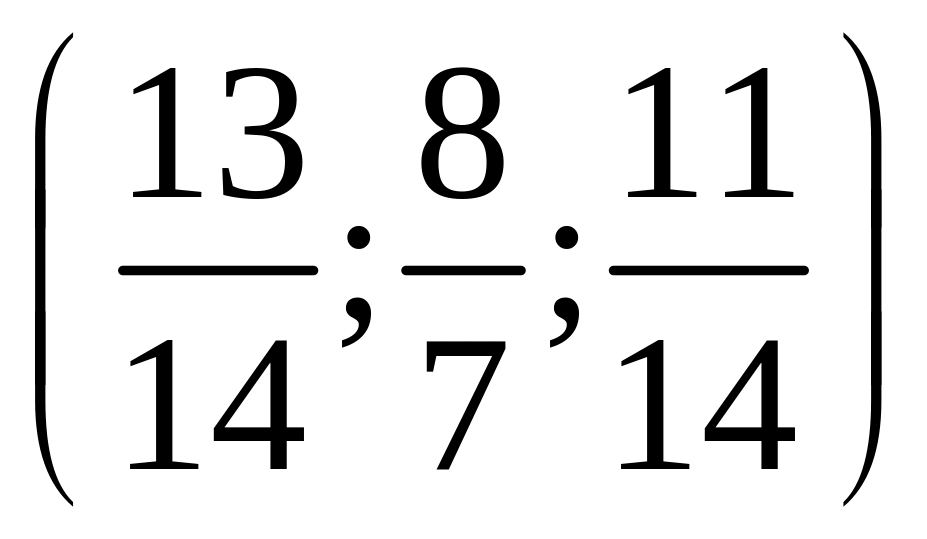 .
.
ТЕСТ по теме: «Элементы векторной алгебры. Линии на плоскости. Поверхности и линии в пространстве.»
К каждому из предложенных ниже заданий дано четыре варианта ответов. Один из предложенных ответов – правильный. Выбрать правильный ответ.
1. Найти длину вектора , если .
Варианты ответов:
а)
1; б)
2;
в) 4;
г)
![]() .
.
2. Найти
координаты вектора
![]() ,
если
,
если
![]() .
.
Варианты ответов:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
3. Найти
скалярное произведение векторов
![]() .
.
Варианты ответов:
а)
![]() ;
б) 16;
в) 8;
г) 4.
;
б) 16;
в) 8;
г) 4.
4. При
каком значении параметра
векторы
![]() перпендикулярны?
перпендикулярны?
Варианты ответов:
а)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
5. Составить
уравнение прямой, проходящей через
точку
перпендикулярно прямой
![]() .
.
Варианты ответов:
а)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
6. Найти
расстояние от точки
![]() до прямой
до прямой
![]() .
.
Варианты ответов:
а)
1;
б) 2;
в) 5;
г)
![]() .
.
7. Найти
проекцию точки
![]() на прямую
на прямую
![]() .
.
Варианты ответов:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
8. Составить
уравнение плоскости, проходящей через
точку
![]() перпендикулярно вектору
перпендикулярно вектору
![]() .
.
Варианты ответов:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
9. Какому
(из ниже перечисленных) векторов
параллельна прямая
![]() ?
?
Варианты ответов:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
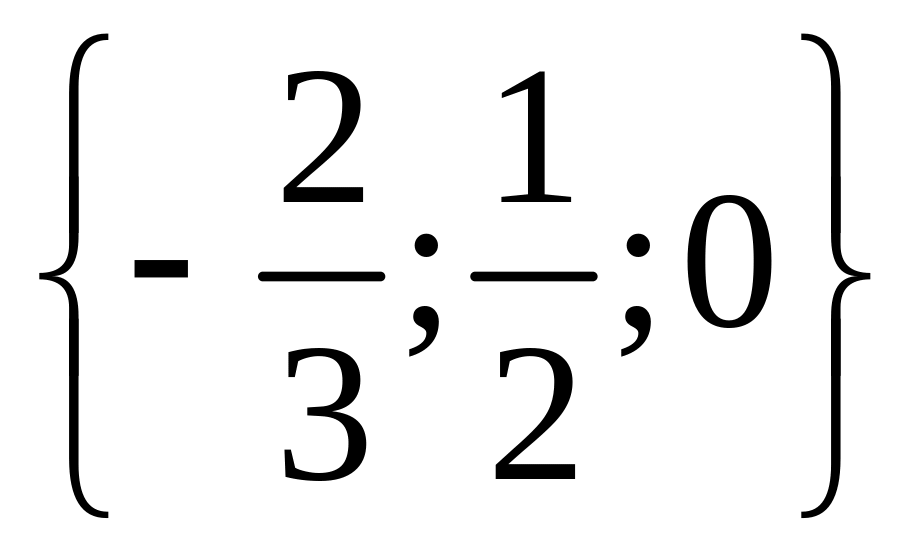 ;
г)
;
г)
![]() .
.
10. Найти
расстояние от точки
![]() до
до
плоскости
![]() .
.
Варианты ответов: а) 2; б) 4; в) 1; г) 3.
11. При
каком значении параметра
![]() прямая
прямая
![]() перпендикулярна плоскости
перпендикулярна плоскости
![]() ?
?
Варианты
ответов: а)
10;
б) 2;
в)
![]() ;
г) нет
такого
.
;
г) нет
такого
.
Правильный ответ:
1.
![]() ;
2.
;
2.
![]() ;
3. 8;
4.
;
5.
;
6.
;
3. 8;
4.
;
5.
;
6.
![]() ;
;
7. ; 8. ; 9. ; 10. 4;
11. 2.
Учебно – методическое пособие
