§ 4. Теорема Гаусса в дифференциальной форме.

Она устанавливает связь между объемной плотностью заряда и изменениями напряженности поляв окрестности данной точки пространства.

Введем дифференц. скалярную характеристику для данной точки векторного поля – дивергенция поля(div).

.

Из математики – теорема Остроградского

т. Гаусса

(13)- Т.Г в дифференц. форме или дифференц. формулировка закона Кулона.

Замечание 1: Выражение для дивергенции зависит от выбора системы координат

- декарт:

- цилиндр: .

Замечание 2: Написание формулы упрощается, если ввести векторныйдифф. оператор(набла), приобретающий смысл в сочетании со скалярной или векторной функцией

= 

декарт  .

Замечание 3: В тех точках поля, где div>0 имеютсяисточники поля (полож. заряды), а где div<0 имеютсястоки поля (отр. Зар.). Линии выходят из источников и заканчиваются в стоках.

§ 5. Применение т. Гаусса для расчета э/ст. Поля.

Положения: При использовании теоремы Гаусса для расчета электрических полей нужно учитывать, что:

1) рассчитать можно только поле, которое обладает специальной симметрией (чаще всего плоской, цилиндрической или сферической).

2) симметрия и конфигурация поля должны быть такими, чтобы можно было найти достаточно простую замкнутую поверхность S (называемую гауссовой поверхностью), такую, чтобы отдельные ее части S_i были параллельны вектору (тогда ) илиотдельные ее части S_j были перпендикулярны и напряженность на них была постоянна по модулю(тогда ).

Если этого нет, задачу о нахождении поля приходится решать помощью метода непосредственного интегрирования или с помощью других методов, с которыми мы ознакомимся ниже.

Рассчитаем:

1. поле бесконечной заряж. равном. плоскости

Дано:

- ?

Рис. 11

Из симметрии задачи вектор  плоскости и в симметр. отн. плоскости точках одинаков. по модулю и противоп. по направлению (Рис. 11 ). Гауссова поверхность – цилиндр. Тогда поток вектора напр. находится как сумма потоков через основания и боковую поверхность.



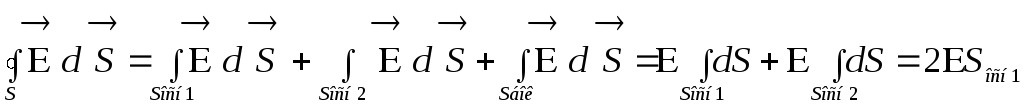
 теор. Г.  напр. равном. заряж. плоскости

2. поле бесконечной равномерно заряженной нити

Дано:

Рис. 12

Из симметрии поле имеет радиальный характер, т.е. вектор напр. в каждой точке цилиндрической поверхности и постоянен на ней по модулю. Эта цилиндрическая поверхн. сносна с нитью

Анализ на боков. поверхность на основ.

Т. Гаусса 

3. поле равномерно заряженной сферич. поверхности

Дано:

R

- ?

Рис. 13

Поле центральной симм. на сферической поверхности.

r > R: на S

Т. Гаусса 

  , r  R

Выражения для напряженности полей заряженных тел (в вакууме), обладающих специальной симметрией, рассчитанных по теореме Гаусса.

Равномерно заряженная с линейной плотностью λ бесконечная нить (полецилиндрической симметрии)	(r — расстояние от нити по перпендикуляру к ней)
Равномерно заряженная зарядом qпо поверхности сфера радиусомR(поле сферической симметрии)	(r — расстояние от центра сферы)
Равномерно заряженная бесконечная плоскость
Заряд равномерно распределен с объемной плотностью ρпо объему шара радиусаR(поле сферической симметрии)	(r — расстояние от центра шара)