§3 Теорема Гаусса.

Вычисление электрического поля в некоторых случая, обладающих специальной симметрией, упрощается применением теоремы Остроградского – Гаусса.

Электростатическая теор. Гаусса устан. матем. связь между потоком вектора напряженности Eсквозь замкнутую поверхностьSи зарядом, находящимся в объеме, ограниченной этой поверхностью.

(стационарн.)

Рис. 7

а) элементарный поток вектора через ориентиров. плоскую элементарную площадку dS () есть скалярная физ. величина, равная скалярному произведениюна(Рис. 7):

(9)

где Е_п— проекция вектора на нормаль к площадке . Выбор направления вектора (а следовательно, и ) условен, его можно было направить и в противоположную сторону.

Замечание: Площадка элементарная, т.е. в пределах нее вектор постоянен.

б) Рассмотрим поверхность S. Разобьем ее на элементарные площадки dS в пределах которых вектор . Поток вект. поля напр. через поверхн.S есть сумма элементарных потоков по всем элементарным площадкамdS из которых состоит поверхность S

(10)

Эта величина алгебраическая. Она зависит не только от конфигурации поля E, но и от выбора нормали поверхн.

Замечание: Если поверхн. S – замкн, то этот факт изображ  , а нормаль и к поверх. берется внешняя (наружу области, охватываемой поверхностью)

I. Теорема Гаусса для точечного заряда

- поле точечного заряда.

Рис8.

а) В качестве замкнутой поверхности возьмем сферу радиуса R (рис. 8)

и на S  наS

(сфера)

б) S – произвольная замкнутая поверхность охватывает заряд (Рис. 9 ). На поверхности S выделим элементарную площадку dS. Проведем к ней радиус-вектор и построим площадкуdS₁, перпендикулярную к . d - это телесный угол, под которым элем. площ. dS₁ видна из начала отсчета (начало отсчета совпадает с зарядом q).

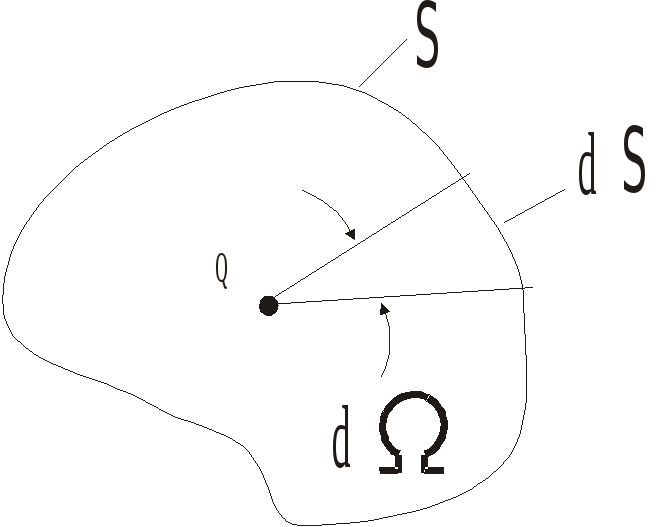
Рис.9

dS₁ = dS·cos,

Теорема Гаусса для точечного заряда:

Поток вект. поля , созд. зар.q через любую замкнутую поверх. S внутри которой находится заряд q равен отношению этого заряда к _o.

Рис. 10

Следствие 1: Если замкн. поверхн. не охват. заряд, то поток через нее равен 0. Ф_Е = 0 (Рис. 10)

НаADB:



На ACB:



Следствие 2: Теорема Гаусса – следствие закона Кулона, т.к. существенным явл-ся зависимость точечного заряда от . Т.Г. является интегральной формулировкой закона Кулона

Замечание: Если имеется одн. эл/ст. поле E, а поверхн. S – плоская, то поток через эту поверхность находится следующим образом:

II. Поле системы точечных зарядов

Обобщ. Т.Г. на систему точечных зарядов производится с помощью принципа суперпозиции: Если имеются заряды q_i, то напряженность в каждой точке есть сумма напряженностейполей, создаваемых каждым из точечных зарядов

(11)

Следствие:

Если заряды распределены непрерывно с объемной плотностью , то поток вектора напряженности:

(12)

V –объем пр-ва, охвачен. поверхностью S:

Замечание 1:

Если само поле Е зависит от конфигурации всех зарядов, поток вектора Е сквозь произвольную замкнутую поверхность S, определяется только зарядами внутри S. Т.е., если передвин. заряды без пересечения поверх. S, то поле изменяется всюду, а поток вектора останется прежним.

Замечание 2: Мощность источников вектора напряженности пропорцион. создаваемому ими полному потоку. Это дает возможность определять местонахождение и мощность источников поля.