
Лекция по физике 2
.pdf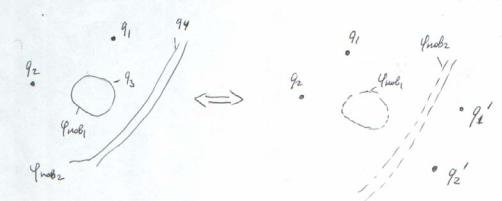
§20. Метод изображений.
ряд задач в эл/статике, при решении которых из соображения симметрии можно угадать ответ. В основе “угадывательных.” методов лежит теорема Единственности решения общей задачи эл/ст., смысл которой состоит в том, что хорошо угаданное решение (распредел. зарядов или поле) есть единственное правильное решение.
Метод изображ. – “угадыват. метод, им решаются задачи”: - любая система зарядов над проводящей плоскости - проводящий шар в поле точечного заряда.
Физическая формулировка теоремы Единственности.
распределение напряж. поля (потенц.) в пространстве вне проводников, при котором поверхности проводников оказываются эквипотенциальными, а заряды (ϕiпов) = заданным значениям.
Метод изображения состоит в определенном (угадывании) поля, создаваемого зарядами в присутствии проводников, путем введения вместо этих проводников фиктивных зарядов qi’ (Рис. 61).
Рис. 61
Результирующее поле оставш. Истинных и фиктивных. зар. должно быть таким, чтобы его эквипотенциальные поверхности совпадали с

поверхностями проводников ϕповi , действие которых заменено фиктивными зарядами.
Можно сказать, что метод изображений по существу основан на подгонке потенциала под граничные условия: мы стараемся найти другую задачу (конфигурацию зарядов), у которой конфигурация поля в интересующей нас части пространства была бы той же. Если это удается сделать с помощью достаточно простых конфигураций, то метод изображений оказывается весьма эффективным.
Примеры 1) Точечный заряд и проводящая плоскость
Когда точечный заряд q находится около безграничной проводящей плоскости (рис. 62, а) действие индуцированных зарядов на плоскости заменяем фиктивным зарядом q’ = -q. Поле этой системы известно (его линии вектора Е показаны на рис. 62, б).
Совместим со средней эквипотенциальной поверхностью (ее потенциал ϕ = 0) проводящую плоскость и уберем заряд -q. Согласно теореме единственности поле в верхнем полупространстве останется прежним. Действительно, на проводящей плоскости и всюду в бесконечности ϕ = 0, точечный же заряд q можно рассматривать как предельный случай малого сферического проводника, радиус которого стремится: к нулю, а потенциал — к бесконечности. Таким образом, в верхнем полупространстве граничные условия для потенциала остались теми же, стало быть, темже осталось и поле вэтой области (рис. 62, в).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
|
б) |
|
в) |
|
|
Рис.62 |
|
|
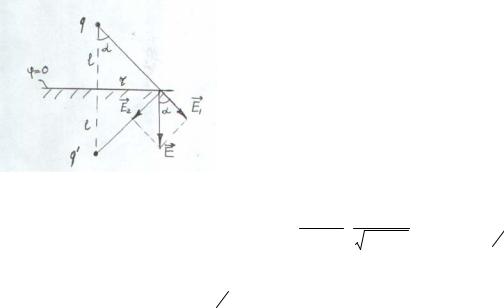
Итак, в рассматриваемом случае поле отлично от нуля только в верхнем полупространстве, и для вычисления этого поля достаточно ввести фиктивный заряд-изображение q' = -q, противоположный по знаку заряду q, поместив его по другую сторону проводящей плоскости на таком же расстоянии от нее, что и заряд q. Фиктивный заряд q создает в верхнем полупространстве точно такое же поле, как и индуцированные заряды на плоскости. Именно это подразумевают, когда говорят, что фиктивный заряд заменяет собой «действие» всех индуцированных зарядов. Надо только иметь в виду, что «действие» фиктивного заряда распространяется лишь на то полупространство, в котором находится действительный заряд q. В другом полупространстве поле отсутствует.
Сила взаимод. между q и зарядом на плоскости будет равна силе взаимодействия q и q’ (Рис. 63)
|
|
|
|
|
|
F = k |
|
q2 |
|
|
|
|
|
Рис. 63 |
|
|
|
(2l)2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
→ |
→ |
→ |
|
|
|
|
|
q |
l |
|
k q l |
|
E |
= E |
+ E2 |
E |
пов |
= 2E cosα = 2 k |
|
= 2 |
|||||
|
|
|
||||||||||
|
1 |
|
|
1 |
l |
2 + r2 |
l2 + r2 |
|
(l2 + r2 )32 |
|||
|
|
|
|
|
|
|
||||||
σпов = −ε0E = 2 |
−k ε0 q l |
||
(l2 + r2 ) |
32 |
||
|
|||
2)Точечный заряд и заземленный шар (Рис. 64). Действие индуцированных зарядов на шаре заменяем фиктивным зарядом q’ , помещенным на расстоянии l от центра шара.
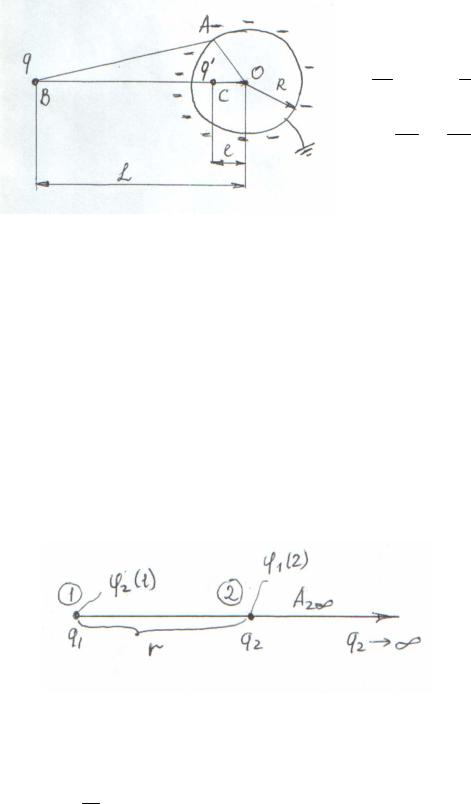
l = R2 ; q/ = −q R L L
ϕA = k q = k q/ AB AC
|
|
|
|
|
|
|
|
|
∆ АОС ~ ∆ ВОА |
АВ |
= |
L |
||||||||
|
|
|
|
|
|
|
|
|
АС |
R |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Рис. 64 |
|
АО |
= |
R |
= |
ВО |
= |
L |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
ОС |
L |
ОА |
R |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ϕA = |
kq |
|
= |
kq/ |
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
AB |
AC |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
q/ = −q |
AC |
= −q |
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
AB |
L |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3) точечный заряд и провод. зар. шар. Найти систему фиктивных зарядов
§ 21. Энергия системы электрических зарядов. п.1. Энергия взаимодействия 2-х точечных зарядов (Рис. 65).
Рис. 65 |
q1 |
– |
|
ϕ (2) = k |
|||
|
|||
1 |
r |
|
|
|
|
потенциал, создаваемый в месте нахождения 2-го заряда зарядом q1
ϕ2 (1) = k qr2 – потенциал, создаваемый в месте нахождения 1-го заряда
зарядом q2
W(r) –потенциальная энергии взаимодействия.
W(r = ∞) = 0 (на бесконечности нет взаимодействия)

|
A2∞ = −∆W =W |
(r) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
(r)= q |
|
|
|
(2)= |
|
kq q |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
2 |
ϕ |
|
|
1 2 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
A2∞ = q2 (ϕ1(2) |
−ϕ∞ ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Замечание: Т.к. у нас |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
W (r)= q |
2 |
ϕ |
(2) |
= |
|
kq1q2 |
= q |
2 |
ϕ (2)= q ϕ |
2 |
(1)= |
1 |
[q |
2 |
ϕ (2) |
+ q ϕ |
2 |
(1)] |
||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
r |
|
|
|
|
|
1 |
1 |
|
|
|
|
2 |
|
1 |
|
1 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
п. 2. Система точечных зарядов. |
||||||||||||||||||||||||
W = ∑Wij |
= |
|
1 |
∑∑Wij |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
i |
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
W |
|
=W |
|
= |
|
qiq j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
4πε r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
ij |
|
|
|
ji |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 ij |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Wij – пот. энергия взаимодействия двух зарядов |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
qiq j |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
q |
|
1 |
|
|
|
|||||||||||
|
|
∑∑Wij |
= |
|
∑∑ |
|
|
= [i ≠ |
|
j]= |
|
∑qi ∑ |
i |
|
|
= |
|
∑qiϕ(i) |
||||||||||||||||||||||||||
|
2 |
2 |
4πε r |
|
|
2 |
4πε |
r |
|
2 |
||||||||||||||||||||||||||||||||||
|
|
i |
|
j |
|
|
|
|
|
|
|
i |
|
|
j |
|
|
0 ij |
|
|
|
|
|
|
|
|
|
|
|
j |
0 |
i |
|
|
|
|
|
|
||||||
ϕi
ϕ(i) – результат пот. всех зарядов в точке, где qi
W = 12 ∑qiϕ(i) = 12 [q1 (ϕ1) +....+qn (ϕn )]
Пример 3.1. Четыре одинаковых точечных заряда q находятся в вершинах тетраэдра с ребром а (рис. 66). Найти энергию взаимодействия зарядов этой системы.
q
q |
q |
q
Рис. 66
Решение. Энергия взаимодействия каждой пары зарядов здесь одинакова и
равна |
W = q2 |
/ 4πε |
0 |
a. |
Всего |
таких |
|
i |
|
|
|
|
взаимодействующих пар, как видно из рисунка, шесть, поэтому энергия взаимодействия всех точечных зарядов
данной системы
W = |
1 |
∑ |
W |
= |
∑ |
q |
ϕ |
= |
1 |
4qϕ = |
1 |
|
6q2 |
. |
2 |
4 |
4 |
2 |
|
|
|
||||||||
|
i |
|
i |
i |
|
|
4πε0 a |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||

Полная энергия взаимодействия. Если заряды распределены непрерывно, то, разлагая систему зарядов на совокупность элементарных зарядов dq и переходя от суммирования в (3.1) к интегрированию, получаем
W = 12 ∫ϕdq, |
(3.2) |
где φ — потенциал, создаваемый всеми зарядами системы в элементе объемом dV.
Пример Четыре точечных заряда qi находятся в вершинах квадрата со стороной а (Рис. 67) . Найти энергию взаимодействия зарядов этой системы.
a, qi
_______
W - ?
q1 = q; q2 = - q; q3 = q; q4 = - q;
|
ϕ(1) = ϕ(3) = −kq |
− kq + |
kq |
|
|
|
|
||||||
|
|
|
|
|
|
a |
|
a |
2a |
|
|
|
|
|
ϕ(2) = ϕ(4) = kq |
+ kq − |
kq |
|
|
|
|
||||||
|
|
|
|
|
|
a |
|
a |
2a |
|
|
|
|
|
досчитать |
|
|
|
|
|
|
Рис. 67 |
|||||
|
|
|
|
|
|
|
|
|
|
|
п.3. Энергия заряженного проводника |
||
|
|
|
|
|
|
|
|
|
|
Разобьем |
поверхность проводника на |
||
|
|
|
|
|
|
|
|
|
точечные заряды ∆qi (Рис. 68) |
||||
|
|
|
|
|
|
|
|
|
|
|
q = ∑∆qi |
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
Рис. 68 |
|
|
|
Тогда энергия проводника есть сумма |
|||||||
|
|
|
|
энергий взаимодействия каждой пары точечных |
|||||||||
|
|
|
|
|
|
|
|
|
|||||
зарядов W = |
1 |
∑∆qi |
ϕ(i) = ϕпов |
1 |
∑∆qi = |
1 |
ϕпов q |
||||||
|
2 |
2 |
|||||||||||
2 |
i |
|
|
|
i |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
W = |
1 |
qϕпов |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|

C = |
|
q |
|
- для уедин. проводника |
|
|
|
|
|
||||||
ϕпов |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
W = |
|
1 |
ϕпов q = |
1 |
C ϕпов2 |
= |
q2 |
для уедин. проводника |
|
|
|||||
2 |
2 |
2C |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
IV. Энергия непрерывно распределенного заряда. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
Разбиваем |
|
непрерывно |
||
ρ |
|
|
|
+ |
|
|
|
|
|
распределенный заряд на точечные |
|||||
|
|
|
|
|
|
dq = ρdV |
dq = ρdV => (Рис. 69) |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
1 |
N |
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
+ |
|
|
|
|
|
W = |
lim∑∆qiϕ(i) = |
∫ρϕdV |
|||
|
|
|
|
|
|
|
|
|
|
2 |
|||||
|
|
|
|
|
|
|
|
|
|
2 ∆V →0 i=1 |
|
||||
Рис. 69
W= 12 ∫ρϕdV
φ– потенциал, создаваемый всеми зарядами системы в элементе объемом dV.
Замечание 1. Если заряд распределен по поверхности =>
|
|
W = |
1 |
∫σϕdS |
|
|
2 |
||||
|
|
|
|
|
|
Замечание 2. |
Формула для энергии при непрерывном распределении |
||||
отличается от формулы для энергии взаимодействующих n точечных
зарядов. Она рассчитывает полную энергию взаимодействия. |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Пусть имеются |
два заряженных |
|||
|
|
|
|
|
q1 |
|
|
|
|
q2 |
|
проводника |
(Рис. |
70) |
||
|
|
|
|
|
|
|
|
|
|
(r>>размеров |
=> |
можно |
||||
|
|
|
|
|
|
|
r>> размеров |
|
рассматривать |
взаимодействие |
||||||
|
|
|
|
|
|
|
|
как точечных зарядов) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
φ1пов |
|
|
φ2пов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 70 |
|
|
|
|
|
|
|||
W |
взаим |
= |
1 |
[q ϕ |
2 |
(1) + q |
2 |
ϕ |
(2)] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
2 |
1 |
|
1 |
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
||
|
∫ρϕdV =W1собств |
|
|
|
|
|
|
|||||||||
W = |
|
+W2собств +Wвзаим = |
|
q1ϕ1пов + |
|
q2ϕ2пов |
|
|
||||||||
2 |
2 |
2 |
|
|
||||||||||||

≠ |
q1 |
≠ |
q2 |
|
c |
|
|||
|
|
c |
2 |
|
1 |
|
|
||
φ – потенциал не только заряда другого проводника, но и собственного заряда проводника.
п.5 Энергия заряженного конденсатора
W = |
1 |
|
dq ϕ = |
1 |
|
|
σdS ϕ + |
1 |
(σ)dS ϕ |
2 |
|||
|
|
|
|
||||||||||
|
2 ∫ |
|
|
2 |
|
попов∫ |
1 |
2 |
попов∫ |
||||
|
|
|
|
|
|
|
|
|
a |
|
|
a |
|
W = |
1 |
|
qV = |
q2 |
|
= |
|
CV 2 |
|
|
|
|
|
2 |
|
2C |
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||
W = ∫dq ϕ - формула для любой системы заряда. Но эта формула
V
неудобна.
§ 22. Энергия электрического поля.
Получим через Е. Рассмотрим плоский конденсатор. Пренебрегая краевыми эффектами, считаем поле однородным
C = εεd0S
V = Ed
W = |
CU 2 |
= |
εε |
S E2d 2 |
= |
εε |
E2 |
Sd = ωэ V |
|
0 |
2d |
0 |
|
||||
2 |
|
|||||||
|
|
|
|
2 |
|
|||
rr
ωэ = εε02E 2 = E 2D , ωэ – объемная плотность энергии эл/ст поля
Энергия эл. поля локализована в самом эл. поле. Это подтверждено опытом.
→ →
W = V∫ωэdV = V∫E2DdV
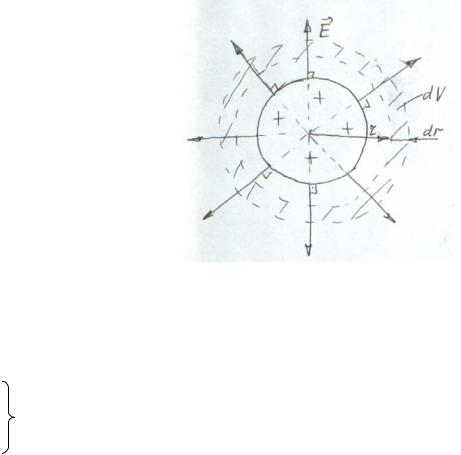
Пример Расчет эл. энергии заряженного шара.
1-ый способ
С = 4πεε0 R
W = |
q2 |
= |
q2 |
|
2C |
8πεε0 R |
|||
|
|
2-ой способ (Рис. 71)
|
q |
, |
r ≥ R |
|
|
|
|||
4πεε0 R |
||||
E = |
|
|
||
|
0, r < R |
|||
|
||||
|
1 |
|
|
|
|
|
|
|
q |
2 |
|
, r ≥ R |
|
||
|
|
|
2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||
ωэ = |
|
εε0 E |
|
= |
|
32π2εε0r4 |
|
n |
|||||||
2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
0, |
r < R |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
∞ |
|
|
q |
2 |
|
|
|
|
2 |
|
q |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
W = ∫ωэdV |
= ∫R |
|
|
|
|
|
|
|
4πr dr = |
|
|
||||
|
|
2 |
|
|
|
4 |
2 |
|
|||||||
V |
|
|
32π εε0r |
|
|
|
|
|
8π εε0 R |
||||||
Рис. 71
п. Работа над полиз. диэлектрика.
|
→ → |
|
|
ε0 E2 |
|
→ → |
|
ωэ = |
E D |
|
ωэ = |
+ |
E P |
||
2 |
|
2 |
2 |
||||
|
|
|
|
|
|||
D = ε0 E+ Pr |
|
|
|
|
|
||
→ |
→ |
|
|
|
|
|
|
§ 23. Энергия системы двух заряженных тел.
→ |
2 |
|
→ |
→ |
|
→ |
2 |
→ |
|
→ |
→ 2 |
|
|
|
|
|
|||
E |
= (E + |
E |
)2 = E |
+ 2 E |
E |
+ E |
2 |
|
|
|
|
|
|
||||||
|
|
|
1 |
2 |
|
1 |
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
W = ω dV = εε0 E1 dV + |
|
εε0 E2 + εε E E dV =W +W +W |
|||||||||||||||||
|
|
∫ |
|
|
∫ 2 |
|
|
|
∫ |
|
2 |
|
|
∫ |
|
→ |
→ |
|
|
|
|
э |
|
|
|
|
|
|
|
0 |
1 |
2 |
1соб 2соб взаим |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
Выводы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1. W > 0 (т.к. Е2 > 0) |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
E12 + E22 > 2 E1E2 W |
|
+W |
|
≥W |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1соб |
|
2соб |
взаим |
|
|||

Собственная энергия заряда обусловлена взаимодействием собственных элементов, среднее расстояние которых друг от друга меньше расстояния.
2.
>
W взаим <= 0
3.При всех возможных перемещениях зарядов, собственная энергия остается постоянной ее можно считать аддитивной постоянной и не учитывать выражения полной энергии.
4.Энергия электрического поля не аддитивная величина.
§24. Силы в электрическом поле.
Все силы, действующие в эл. поле – силы, действ. На заряд. Т. к. силы вызывают механические перемещения иногда их называют пондеромоторными (механическими).
I). Сила, действующая на точечный заряд.
→ |
→ → |
F |
= q E = −q ϕ |
II). Силы, действующие на проводник
В случае заряженного проводника все эл. силы св-ся по взаимному отталкиванию элементов заряда этого проводника. Т.к. элементы не могут покинуть провод, то к его поверхности будут приложены механические силы, стремящиеся его растянуть.
Такие же силы будут приложены к поверхности проводника, помещенного во внешнее поле.
Рассмотрим случай, когда заряженный участок поверхности проводника граничит с вакуумом. На малый элемент ∆S поверхности проводника действует сила
∆F =σ∆S E0 ,
