Задача 244

На стеклянную пластину положена выпуклой стороной плосковыпуклая линза. Сверху линза освещена монохроматическим светом длиной волны нм. Найти радиус R линзы, если радиус четвертого, темного кольца Ньютона в отраженном свете мм.

Дано:

нмм; ; ммм

Решение

Радиус темных колец Ньютона в отраженном свете определяется по формуле [2, с.331]

, (1)

где – номер кольца (); по условию задачи ;

– радиус кривизны поверхности линзы;

– длина волны падающего света.

Из уравнения (1) находим радиус линзы

Подставляя в (2) числовые данные, получим

м.

Ответ: м.

Задача 254

На дифракционную решетку, содержащую штрихов на миллиметр, падает нормально белый свет. Спектр проецируется помещенный вблизи решетки линзой на экран. Определить длину l спектра первого порядка на экране, если расстояние от линзы до экрана м. Границы видимого спектра: нм, нм.

Дано:

мм-1; м; нмм; нмм

Решение

Искомая длина спектра первого порядка на экране будет равна (рис.2)

,

где – расстояние от центра дифракционной картины на экране до максимума 1 порядка фиолетового света;

– расстояние от центра дифракционной картины на экране до максимума 1 порядка красного света.

Рис.2. Схема к задаче 254

Из прямоугольных треугольников и имеем

;

,

где и – углы между нормалью к поверхности решетки и направлением дифрагированных соответственно фиолетовых и красных волн.

Тогда искомая длина спектра будет равна

. (1)

Для определения величин углов и запишем условия главных максимумов при дифракции света на дифракционной решетке (формула [2, с.341])

,

где – период (постоянная) дифракционной решетки;

ммм;

– порядок спектра; по условию задачи .

Таким образом, для фиолетовой части белого света будем иметь

,

откуда

.

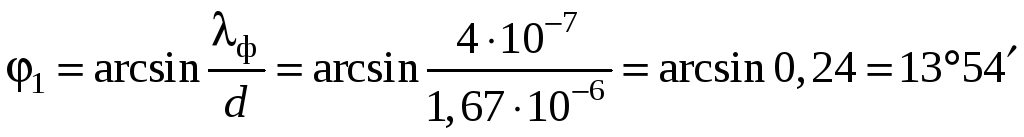Аналогично для красной части белого света получим

.

Таким образом, окончательно получим

ммм.

Ответ: мм

Задача 264

При прохождении света через трубку длиной см, содержащую раствор сахара концентрацией %, плоскость поляризации света повернулась на угол . В другом растворе сахара, налитом в трубку длиной см, плоскость поляризации повернулась на угол . Определить концентрацию второго раствора.

Дано:

см; ; %; см;

Решение

Запишем значения массовых концентраций раствора сахара, используя исходные данные: кг/м³, кг/м³.

Воспользуемся формулой определения угла поворота плоскости поляризации в растворах [2, с.349]

, (1)

где – постоянная вращения;

– массовая концентрация оптически активного вещества (сахара) в растворе;

– длина пути, пройденного светом в растворе сахара.

Для условия задачи будем иметь

, (2)

. (3)

Разделив почленно (2) на (3), получим

;

,

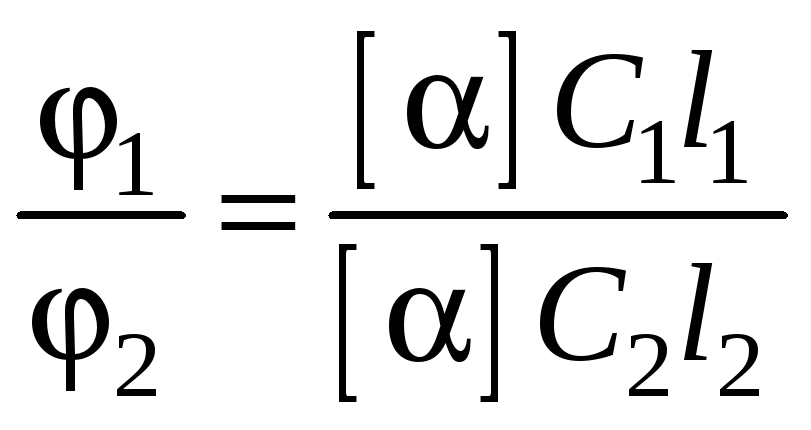откуда получим

. (4)

Подставляя в (4) числовые данные, находим

.

Ответ: .

Задача 274

Мощность излучения абсолютно черного тела равна 10 кВт. Найти величину излучающей поверхности тела, если известно, что длина волны, на которую приходится максимум плотности энергии, равна см.

Дано:

кВтВт; смм

Решение

Поток излучения абсолютно черного тела

, (1)

где - энергетическая светимость абсолютно черного тела;

- площадь поверхности абсолютно черного тела.

Энергетическая светимость абсолютно черного тела согласно закону Стефана-Больцмана выражается формулой [2, с.360]

, (2)

где Вт/(м²К⁴) – постоянная Стефана-Больцмана;

- термодинамическая температура.

Подставляя (2) в (1), получим

,

откуда искомая площадь излучающей поверхности будет равна

. (3)

Согласно закону смещения Вина имеем [2, с.360]

, (4)

где м∙К – постоянная закона смещения Вина;

– термодинамическая температура.

Выражаем из формулы (4) температуру и подставляем в (3). Тогда последовательно получим

;

;

.

Выполняем вычисления

м²см².

Ответ: см².