Задача №14, схема XIV

Для двухопорной балки (рис. 1) определить реакции опор, построить эпюры поперечных сил, изгибающих моментов и подобрать необходимый размер d сечения деревянной балки, составленной из двух круглых брусьев. Для дерева [σ] = 10 МПа = 10 Н/мм². Необходимые исходные данные приведены в таблице 1.

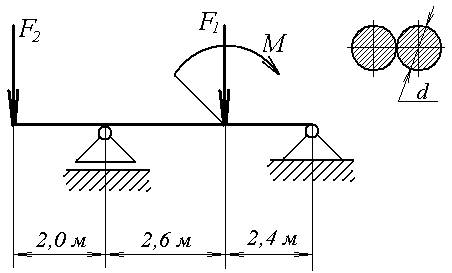
Рис. 1

Таблица 1 – Исходные данные

F1, кН	F2, кН	М, кН·м
9,9	22,7	1,8

Решение:

Изгиб прямых брусьев вызывается парами сил или силами перпендикулярными к его продольной оси. При таком виде деформации в поперечном сечении тела (балки) возникают два внутренних силовых фактора: поперечная сила Q_X и изгибающий момент Ми. Поперечная сила равна алгебраической сумме внешних сил, действующих по одну сторону от рассматриваемого сечения:

Q_y = ΣF_i

Изгибающий момент численно равен алгебраической сумме моментов сил по одну сторону от рассматриваемого сечения:

Ми = Σ М₀(F_i)

Для построения эпюр сначала необходимо определить реакции опор балки. В нашем случае балка расположена на двух опорах, шарнирно подвижной и шарнирно неподвижной, условно покажем направление их реакций на рисунке 2. Если реакция получится со знаком минус, то это будет означать, что мы не угадали её направление, т.е. сила в действительности будет направлена в обратную сторону.

Рис. 2

В шарнирно неподвижной опоре D возникают две реакции, но второй пренебрегаем, так как в наших расчетах она равна нулю, потому что направление вектора совпадает с осью балки и пересекается с центрами опор: ΣF_x = 0 => R_Dx = 0.

Для определения реакций опор балки R_B, R_D составим систему уравнений моментов относительно опоры B и D.

ΣМ_B(F_i) = 0 => –2,0·F₂ – 5,0·R_D + 2,6·F₁ + M = 0

ΣМ_D(F_i) = 0 => –2,4·F₁ + М + 5,0·R_B – 7,0·F₂ = 0

Отсюда находим реакции опор:

R_D = (–2,0·F₂ + 2,6·F₁ + M) / 5,0 = (–2,0·22,7 + 2,6·9,9 + 1,8) / 5,0 = –3,57 кН

R_B = (2,4·F₁ – М + 7,0·F₂) / 5,0 = (2,4·9,9 – 1,8 + 7,0·22,7) / 5,0 = 36,17 кН

Знак минус реакции опоры R_D означает, что мы не угадали ее направление, т.е. сила в действительности направлена в обратную сторону, как показано на рисунке 3.

Рис. 3

Проведем проверку по алгебраической сумме проекций всех внешних сил на ось перпендикулярную балке:

–R_D + R_В – F₂ – F₁ = 0

–3,57 + 36,17 – 22,7 – 9,9 = 0

0 = 0

Реакции опор определены правильно.

Для построения эпюры поперечных сил в соответствии с местом приложения нагрузок — пары сил с моментом М, сосредоточенных сил F₁, F₂ и реакций опор R_D, R_В, разделим балку на три участка: I, II, III (рис. 4). Так как все участки балки свободны от распределенной нагрузки, то поперечные силы на каждом участке постоянны и эпюра Q_y изобразится прямыми линиями, параллельными базовой линии.

Рис. 4

Определим значения поперечных сил на каждом участке, применяя метод сечения начиная от правого конца балки.

Q_yIII = R_D = 3,57 кН;

Q_yII = F₁ + R_D = 9,9 + 3,57 = 13,47 кН;

Q_yI = F₁ + R_D – R_В = 9,9 + 3,57 – 36,17 = –22,7 кН.

По полученным данным строим эпюру Q_y (рис. 5).

Рис. 5

Для построения эпюры изгибающих моментов Ми, применяя метод сечений, вычислим значения изгибающих моментов в характерных точках. При этом можно рассматривать равновесие как левой, так и правой отсеченной части — результаты будут одинаковы.

М_А = 0;

М_В = –2,0·F₂ = –2,0·22,7 = –45,4 кН·м;

М_С^слева = –4,6·F₂ + 2,6·R_B = –4,6·22,7 + 2,6·36,17 = –10,38 кН·м;

М_С^справа = –4,6·F₂ + 2,6·R_B + М = –4,6·22,7 + 2,6·36,17 + 1,8 = –8,58 кН·м;

М_D = –7,0·F₂ + 5,0·R_B + М – 2,4·F₁ = –7,0·22,7 + 5,0·36,17 + 1,8 – 2,4·9,9 = 0;

По полученным данным строим эпюру Ми (рис. 6).

Рис. 6

Рассматривая эпюры и нагрузки на балку с точки зрения общих правил построения эпюр, видим, что построенные эпюры не содержат принципиальных ошибок. Например, там где Q < 0 (участок I), момент Ми убывает; где Q > 0 (участок II и III), изгибающий момент возрастает. На эпюре Q в сечениях, где приложены силы и реакции, имеет место скачок, равный значению этой силы, а на эпюре Ми — излом, острие которого направлено против действия силы. В сечении С, где приложена пара сил, на эпюре Ми наблюдается скачок, равный моменту этой пары, а в эпюре Q нет никаких изменений.

Из условия прочности на изгиб через наибольший изгибающий момент в сечении балки определим её диметр, выразив его из формулы условия прочности:

σ = |Ми_max| / Wx ≤ [σ],

где

Wx = 0,1·d³

отсюда

d ≥ ,

Исходя из условия задачи, заданная балка состоит из двух брусьев, поэтому выражение примет вид:

d ≥ ,

d ≥ = 283 мм

Мы получили, что диаметр одного бруса составной балки для данного условия прочности не должен быть меньше 283 мм.