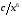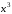контрольная работа (вариант 1)

Министерство образования Республики Беларусь

Учреждение образования

Белорусский государственный университет

информатики и радиоэлектроники

Институт информационных технологий

Специальность: Информационные системы и технологии (в экономике)

КОНТРОЛЬНАЯ РАБОТА

по курсу «Теория вероятностей и математическая статистика»

Вариант №1

Выполнил:

Минск 2010

1.9. Телефонный номер состоит из шести цифр, каждая из которых равновозможно принимает значения от 0 до 9. Найти вероятность того, что все цифры одинаковы.

Решение:

Число возможных комбинаций 10⁶. Число благоприятствующих исходов 10. Значит искомая вероятность:

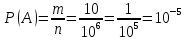
Ответ: 10^-5.

2.23. В задаче приведены схема соединения элементов, образующих цепь с одним входом и одним выходом. Предполагается, что отказы элементов являются независимыми в совокупности событиями. Отказ любого из элементов приводит к прерыванию сигнала в той ветви цепи, где находится данный элемент. Вероятности отказа элементов 1, 2, 3, 4, 5 соответственно равны p1=0,1; p2=0,2; p3=0,3; p4=0,4; p5=0,5. Найти вероятность того, что сигнал пройдет со входа на выход.

I

II

III

Решение:

Найдём вероятность прохождения сигнала по первой ветви:

P₁(A) = 1 – p₁ = 1 – 0,1 = 0,9

P₂(A) = 1 – p₂ = 1 – 0,2 = 0,8

P_I(A∩B) = P₁(A) * P₂(B) = 0,9 * 0,8 = 0,72

Найдём вероятность прохождения сигнала по второй ветви:

P₃(A) = 1 – p₃ = 1 – 0,3 = 0,7

P₄(A) = 1 – p₄ = 1 – 0,4 = 0,6

P_II(A∩B) = P₃(A) * P₄(B) = 0,7 * 0,6 = 0,42

Найдём вероятность прохождения сигнала от входа до выхода:

P(AUBUC) = P(A) + P(B) +P(C) – P(A∩B) – P(B∩C) – P(A∩C) + P(A∩B∩C) = 0,72 + 0,42 + 0,5 – (0,72 * 0,42) – (0,42 * 0,5) – (0,72*0,5) + 0,72 * 0,42 * 0,5 = 1,64 – 0,3024 – 0,21 – 0,36 + 0,1512 = 0,9188

Ответ: 0,9188.

3.14. В тире имеется три ружья, вероятности попадания из которых соответственно равны 0,5; 0,7; 0,9. Определить вероятность попадания при одном выстреле, если ружье выбрано наугад.

Решение:

Вероятность выбора каждого ружья будет равна P(A)= . Для каждого ружья эта вероятность одинакова. Тогда вероятность попадания при одном выстреле, если ружьё было выбрано наугад, вычислим по формуле математического ожидания M(x):

M(x) = x₁*p₁ + x₂*p₂ + x₃*p₃,

где x₁, x₂, x₃ – значения вероятностей попадания из первого, второго и третьего ружей соответственно, равные 0,5; 0,7 и 0,9.

p₁, p₂, p₃ – в данном случае вероятность выбора каждого из ружей.

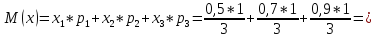
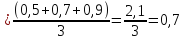
Ответ: 0,7.

4.5. Вероятность изготовления изделия отличного качества равна 0,9. Изготовлено 50 изделий. Чему равны наивероятнейшее число изделий отличного качества и вероятность такого числа изделий отличного качества?

Решение:

Пусть p-вероятность изготовления изделия отличного качества (p=0,9). Тогда q=1-p – вероятность изготовления изделия качества хуже отличного. Тогда для k – наивероятнейшего числа изделий отличного качества:

np – q ≤ k < np + p,

где n – количество изготовленных деталей (n = 50).

50*0,9 – 0,1 ≤ k < 50*0,9 + 0,9

44,9 ≤ k < 45,9

Наивероятнейшее число изделий 45.

Теперь найдём вероятность изготовления такого числа изделий отличного качества с помощью формулы Бернулли.

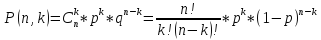
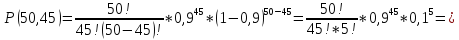
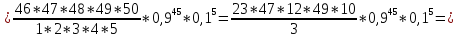
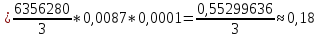
Ответ: 45; 0,18.

5.7. Дискретная случайная величина Х может принимать одно из пяти фиксированных значений x₁, x₂, x₃, x₄, x₅ с вероятностями p₁, p₂, p₃, p₄, p₅ соответственно (конкретные значения приведены в табл.). Вычислить математическое ожидание и дисперсию величины Х. Рассчитать и построить график функции распределения.

Вариант	x1	x2	x3	x4	x5	p1	p2	p3	p4	p5
5.7	-5	-2	0	1	2	0,5	0,1	0,1	0,2	0,1

Решение:

Математическое ожидание.

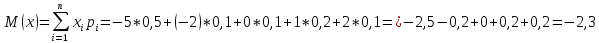
Дисперсия.

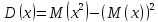
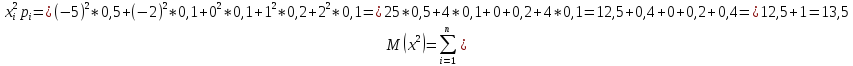
Функция распределения.

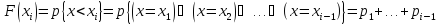
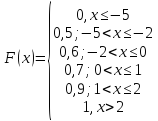
6.28. Случайная величина Х задана плотностью вероятности

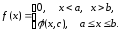
Определить константу С, математическое ожидание, дисперсию, функцию распределения величины Х, а также вероятность ее попадания в интервал.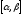

Вариант	x,c)	a	b		
6.28		1	2	0	1,5

Решение:

Для определения постоянной воспользуемся свойством плотности вероятности:

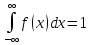
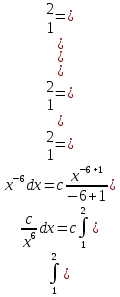
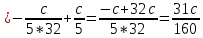
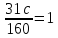
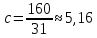
Математическое ожидание.

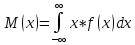
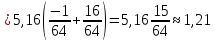
Дисперсия.

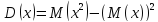
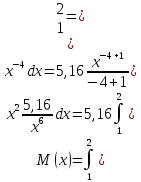
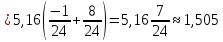
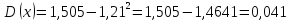
Вероятность того, что 0 < x < 1,5

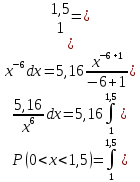
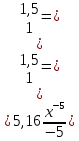
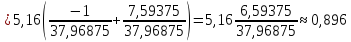
Функция распределения.

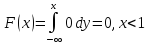
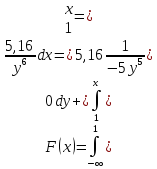
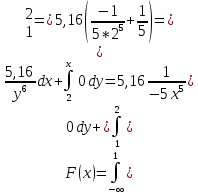
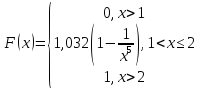
7.6. Случайная величина Х распределена равномерно на интервале [a,b]. Построить график случайной величины Y=(X) и определить плотность вероятности g(y).

Вариант		a	b
7.6		-1	2	5

Решение:

Плотность вероятности случайной величины X найдём по формуле:

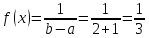
Обратная функция:

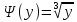
График f(x):

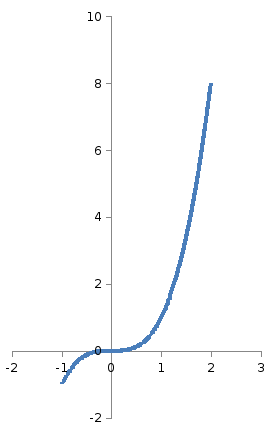
(-∞, -1) k = 0

(-1, 8) k = 1

(8, +∞) k = 0

Т.к. на интервалах (-∞, -1) и (8, +∞) обратная функция не существует, то g(y) = 0.

В интервале (-1, 8) одна обратная функция 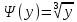следовательно

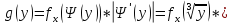
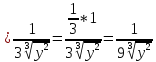
Таким образом, плотность вероятности величины y равна:

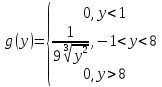
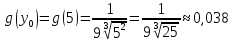
8.23. Двумерный случайный вектор (Х, У) равномерно распределен внутри выделенной жирными прямыми линиями на рис. области B. Двумерная плотность вероятности f(x,y) одинакова для любой точки этой области B:

Вычислить коэффициент корреляции между величинами X и Y.

Вариант	x1	x2	x3	x4	x5	x6	y1	y2
8.23	0	0	2	4	2	0	1	2

Решение:

Совместная плотность вероятности примет вид:

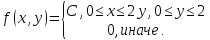
Неизвестную константу C определим, используя условие нормировки плотности вероятности:

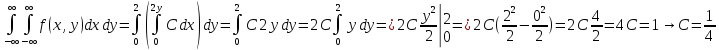
Таким образом:

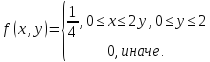
Вычислим математические ожидания:

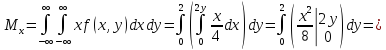
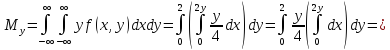
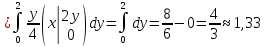
Вычислим дисперсии:

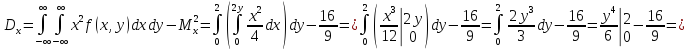
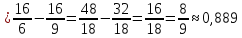
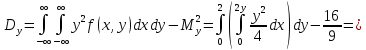
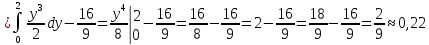
Корреляционный момент:

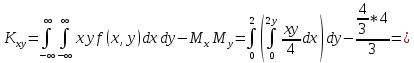
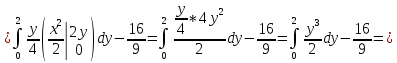
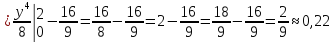
Коэффициент корреляции:

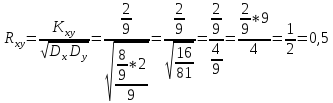
9. Одномерная выборка.

-0.51 -0.11 0.51 2.51 3.07 2.20 1.86 4.14 3.29 5.03 5.60 5.10 2.95 -0.45 1.74 2.18 -0.47 5.72 6.08 -0.15 2.64 5.97 2.22 -0.42 5.48 2.67 5.56 5.55 4.50 3.91 0.17 2.07 0.09 2.62 6.00 2.55 1.09 2.10 3.47 6.14 3.26 -0.22 3.35 6.15 1.96 6.14 -0.42 5.45 5.87 0.27 0.58 2.63 -0.42 4.79 2.93 2.78 2.32 0.92 4.20 -0.31 3.83 6.10 3.89 0.29 3.04 4.37 4.11 0.77 1.95 0.73 3.34 2.14 -0.15 2.17 4.99 5.31 0.65 2.32 3.45 2.12 -0.28 0.86 0.19 0.87 0.63 1.45 2.16 4.19 4.56 2.60 4.02 1.72 5.41 3.46 5.28 0.78 5.06 1.43 6.00 4.42

- получить вариационный ряд;

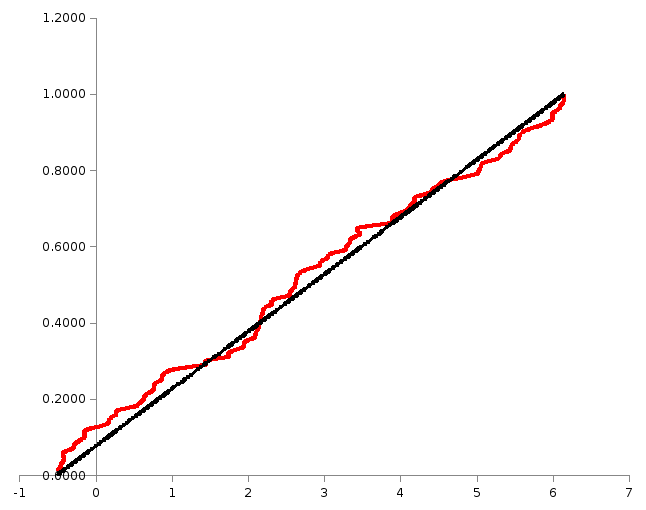
- построить на масштабно-координатной бумаге формата А4 график эмпирической функции распределения F*(x);

- построить гистограмму равноинтервальным способом;

- построить гистограмму равновероятностным способом;

- вычислить оценки математического ожидания и дисперсии;

- выдвинуть гипотезу о законе распределения случайной величины и проверить ее при помощи критерия согласия и критерия Колмогорова (α=0,05).

Решение:

Вариационный ряд:

Номер	X		39	2,14		78	4,79
1	-0,51		40	2,16		79	4,99
2	-0,47		41	2,17		80	5,03
3	-0,45		42	2,18		81	5,06
4	-0,42		43	2,2		82	5,1
5	-0,42		44	2,22		83	5,28
6	-0,42		45	2,32		84	5,31
7	-0,31		46	2,32		85	5,41
8	-0,28		47	2,51		86	5,45
9	-0,22		48	2,55		87	5,48
10	-0,15		49	2,6		88	5,55
11	-0,15		50	2,62		89	5,56
12	-0,11		51	2,63		90	5,6
13	0,09		52	2,64		91	5,72
14	0,17		53	2,67		92	5,87
15	0,19		54	2,78		93	5,97
16	0,27		55	2,93		94	6
17	0,29		56	2,95		95	6
18	0,51		57	3,04		96	6,08
19	0,58		58	3,07		97	6,1
20	0,63		59	3,26		98	6,14
21	0,65		60	3,29		99	6,14
22	0,73		61	3,34		100	6,15
23	0,77		62	3,35		Среднее	0,628684
24	0,78		63	3,45
25	0,86		64	3,46
26	0,87		65	3,47
27	0,92		66	3,83
28	1,09		67	3,89
29	1,43		68	3,91
30	1,45		69	4,02
31	1,72		70	4,11
32	1,74		71	4,14
33	1,86		72	4,19
34	1,95		73	4,2
35	1,96		74	4,37
36	2,07		75	4,42
37	2,1		76	4,5
38	2,12		77	4,56

Строим график эмпирической функции распределения F*(x):

Строим гистограмму равноинтервальным способом. Для этого определим необходимое количество интервалов

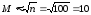
j	Aj	Bj	hj	vj	p*j	f*j
1	-0,51	0,16	0,666	13	0,13	0,1952
2	0,16	0,82	0,666	11	0,11	0,1652
3	0,82	1,49	0,666	6	0,06	0,0901
4	1,49	2,15	0,666	9	0,09	0,1351
5	2,15	2,82	0,666	15	0,15	0,2252
6	2,82	3,49	0,666	11	0,11	0,1652
7	3,49	4,15	0,666	6	0,06	0,0901
8	4,15	4,82	0,666	7	0,07	0,1051
9	4,82	5,48	0,666	9	0,09	0,1351
10	5,48	6,15	0,666	13	0,13	0,1952