Числові характеристики випадкової величини (математичне сподівання, дисперсія) та їх властивості.
Функції розподілу ймовірностей як для дискретних, так і для неперервних випадкових величин дає повну інформацію про них. Проте на практиці немає потреби так докладно описувати ці величини, а достатньо знати лише певні параметри, що характеризують їх істотні ознаки. Так, наприклад, при вивченні розподілу заробітної платні цікавляться, по-перше, середньою платною та характеристикою розсіювання. Ці параметри й називають числовими характеристиками випадкових величин.
5.1.1 МАТЕМАТИЧНЕ СПОДІВАННЯ
Однією з найчастіше застосовуваних на практиці характеристик є математичне сподівання (позначається ).
Термін «математичне сподівання» випадкової величини є синонімом терміна «середнє значення» випадкової величини .
ОЗНАЧЕННЯ 5.1. Математичним сподіванням випадкової величини , визначеною на дискретному просторі , називається величина (сума ряду):
;
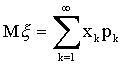в тому випадку, коли цей ряд збігається абсолютно.
Якщо - обмежена множина, то
.
ОЗНАЧЕННЯ 5.2. Математичним сподіванням випадкової величини , визначеною на неперервному просторі , називається величина
,
якщо цей інтеграл збігається абсолютно.
Якщо = (- , то
.
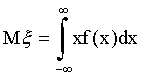Якщо = , то
.
5.1.2 ВЛАСТИВОСТІ МАТЕМАТИЧНОГО СПОДІВАННЯ
ТЕОРЕМА 5.1. (Властивості математичного сподівання).
1. Математичне сподівання від сталої величини С дорівнює самій сталій:
М(С) = С.
2. Сталу величину можна виносити за знак математичного сподівання, тобто якщо - випадкова величина, а С - стала, тоді
М(С) = С.
3. Нехай -
дискретна випадкова величина,
математичне сподівання якої означене.
Тоді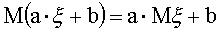 
, де a та b -
постійні.
ДОВЕДЕННЯ:
1. Справді, сталу С можна розглядати як випадкову величину, що з імовірністю, яка дорівнює одиниці, набуває значення С, а тому
М(С) = С 1 = С.
2. На підставі означень 5.1 та 5.2, згідно властивостей суми та інтегралу маємо:
- для дискретної випадкової величини
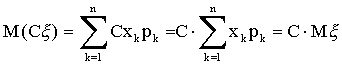
- для неперервної:
3.
Зауважимо, що коли 
-
дискретні випадкові величини
і 
- борелівська функція n змінних,
то суперпозиція 
-
теж дискретна випадкова величина.
Нехай дискретна випадкова величина має розподіл
:
.
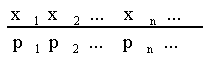Тоді
випадкова величина 
має
розподіл
: 
.
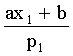
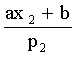
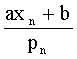
Оскільки
ряд 
абсолютно
збігається, тому ряд
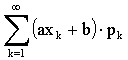теж
абсолютно збігається, і
Для неперервної випадкової величини:
Зауважимо, що коли випадкова величина а;b, то М() а;b, а саме: математичне сподівання випадкової величини обов'язково міститься всередині інтервалу а;b, яке являє центр розподілу цієї величини.
ТЕОРЕМА 5.2. Нехай , - дискретні випадкові величини, математичні сподівання яких скінченні. Тоді + має скінчене математичне сподівання і
ОЗНАЧЕННЯ 5.3. Дві дискретні випадкові величини , з розподілами
:
та
: 
називають незалежними,
якщо події 
та 
незалежні
для будь-яких 
, тобто
ТЕОРЕМА
5.3. Якщо 
незалежні
дискретні випадкові величини зі
скінченими
математичними
сподіваннями, то випадкова величина
(дискретна) 
має
скінчене
математичне сподівання
.
ДОВЕДЕННЯ: Нехай мають розподіли як в означенні 5.3.
Випадкова
величина приймає
значення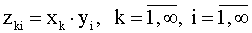 
(не
всі, можливо, рівні) з ймовірностями
(з
огляду на незалежність
).
Оскільки
ряди 
та 
абсолютно
збіжні, то подвійний ряд 
теж
абсолютно збіжний, і тоді
.
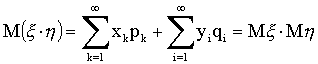ДИСПЕРСІЯ ТА СЕРЕДНЄ КВАДРАТИЧНЕ ВІДХИЛЕННЯ
Розглянемо випадкові величини, які мають різні закони розподілу, але їх, математичні сподівання однакові. Отже, математичне сподівання не дає достатньо повної інформації про випадкову величину, оскільки одному й тому самому значенню М() може відповідати безліч випадкових величин, які будуть різнитися не лише можливими значеннями, а й характером розподілу та самою природою можливих значень.
Приклад 5.9.
Для вимірювання розсіювання вводиться числова характеристика, яку називають дисперсією.
Щоб визначити дисперсію, розглянемо випадкову величину:
- відхилення
випадкової величини від свого
математичного сподівання
=
( - М ()).
Математичне
сподівання випадкової величини 
завжди
дорівнює нулю. Справді,
М(
)
= М( - М ()) = M() - M(М
()) = M() - M() = 0.
Отже, відхилення не може бути мірою розсіювання випадкової величини.
ОЗНАЧЕННЯ 5.6. Дисперсією випадкової величини називається математичне
сподівання квадрата відхилення цієї величини від свого математичного сподівання
D() = М[ - М ()]2 .
|
|
|
|
Для дискретної випадкової величини дисперсія обчислюється за формулою:
|
|
|
|
Для неперервної випадкової величини дисперсія обчислюється за формулою:
Якщо випадкова величина виміряна в деяких одиницях, то дисперсія вимірюватиметься в цих самих одиницях, алеув квадраті.
Тому доцільно мати числову характеристику такої самої вимірності, як і випадкова величина. Тому разом з дисперсією, як мірою розсіювання випадкової величини (для вимірювання розсіювання) уводиться також числова характеристика, яку називають середнє квадратичне відхилення.
|
|
|
|
Середнім квадратичним відхиленням випадкової величини називають корінь квадратний з дисперсії:
5.1.5 ВЛАСТИВОСТІ ДИСПЕРСІЇ
ТЕОРЕМА 5.4. (Властивості дисперсії).
1. Для будь якої випадкової величини вірно D 0.
2. Якщо С - стала величина, то D( C ) = 0.
3. Якщо c - стала величина, то D(c) = c2 D.
4. Якщо a i b - сталі величини, то D(a + b) = a2 D.
5. Якщо випадкові величини і незалежні, тоді
D( ) = D + D.
ДОВЕДЕННЯ: Властивості 1 - 5 можна довести згідно властивостей математичного сподівання.
Справді:
1. D()
= М[ - М ()]2 = М(
) 0,
так як
0,
то це вірно згідно властивостей суми
та інтегралу.
2. D(С) = М[С - М (С)]2 = М[С - С]2 = М(0) = 0.
3. D(c) = М[c - М (c)]2 = М[c - cМ ()]2 =М[c( - М ())]2 =
= c2М[ - М ()]2 = c2D().
4. Згідно властивостей 2 та 3 маємо:
D(a + b) = М[а + b - М(а + b)]2 = М[а + b - аМ() - b]2 =
= М[а( - М()]2 = a2М[ - М()]2 = a2 D.
6. Зауважимо, що дисперсію, спідручніше, можна обчислити за формулою:
7.
D = M2 - (M)2. (*)
Справді,
D = M(- M)2 = M[2 - 2M + (M)2] = M2 - 2MM + (M)2] =
= M2 - (M)2.
маємо
D( + ) = M[( + ) - M ( + )]2 = M[( - M) +( - M)]2 =
= M( - M)2 +M( - M)2 + 2 М[( - M) ( - M)],
але випадкові величини і незалежні, тоді ( - M) і ( - M) теж незалежні, і тоді М[( - M) ( - M)] = М( - M) М( - M) = 0.
Звідси маємо
D( + ) = M( - M)2 +M( - M)2 = D + D;
D( - ) = D( + (-)) = D + D(-) = D + (-1)2 D D + D.