3. Умовна ймовірність. Формула повної ймовірності. Формули Бейєса.

Умо́вна ймові́рність — ймовірність однієї події за умови, що інша подія вже відбулася.

Нехай   — фіксований ймовірнісний простір. Нехай   дві випадкової події, причому  . Тоді умовною ймовірністю події A при умові події Bназивається

Властивості

Прямо з визначення очевидно випливає, що

Якщо  , то умовна ймовірність, строго кажучи, не визначена. Проте іноді умовляються вважати її в цьому випадку рівною нулю .

Умовна ймовірність є ймовірністю, тобто функція  , задана формулою

задовольняє всім аксіомам імовірнісної міри.

Формула повної ймовірності дозволяє обчислити ймовірність деякої події через умовні ймовірності цієї події в припущенні якихось гіпотез, а також ймовірностей цих гіпотез.

Визначення

Нехай дано імовірнісний простір  , і повна група подій  , таких що  . Хай   подія, що цікавить нас. Тоді

.

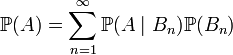Зауваження

Формула повної ймовірності також має наступну інтерпретацію. Нехай N - випадкова величина, що має розподіл

.

Тоді

,

тобто апріорна ймовірність події рівна середньому його апостеріорній ймовірності.

Теоре́ма Ба́єса — одна з основних теорем теорії ймовірностей, яка визначає ймовірність настання події, коли відома тільки часткова інформація про подію. Названа на честьТомаса Баєса.

Формула Баєса:

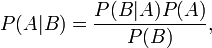
де

P(A) — апріорна ймовірність гіпотези A;

P(A | B) — ймовірність гіпотези A при настанні події B (апостеріорна ймовірність);

P(B | A) — ймовірність настання події B при істинності гіпотези A;

P(B) — ймовірність настання події B.

Формула виводиться із визначення умовної ймовірності:

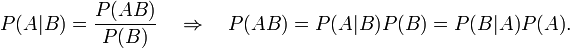
Наслідок

Важливим наслідком формули Баєса є формула повної ймовірності події, що залежить від декількох несуміснних гіпотез (і тільки від них).

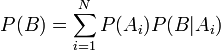 — ймовірність настання події B, що залежить від гіпотез A_i, якщо відомі їх ступені достовірності.

4. Схема незалежних випробувань. Граничні теореми.

Схема незалежних випробувань Бернуллі

Проводяться n дослідів, у кожному з яких може настати певна подія ("успіх") з ймовірністю p (або не настати - "неуспіх" - q = 1 - p). Знайти ймовірність отримати k успіхів у досліді.

Нехай при незмінних умовах проводяться послідовні пов-торні випробування, в результаті яких можуть бути два мож-

ливі наслідки (дві елементарні події А і A ): певна подія А

відбувається і не відбувається A . Оскільки імовірність події А в кожному випробуванні не залежить від наслідку (ре-зультату) інших випробувань, то такі випробування нази-вають незалежними. Якщо в кожному незалежному випро-буванні імовірність настання події А одна й та сама і дорівнює р (0 < р < 1) і не залежить від номера випробування, то такі випробування називаються схемою Бернуллі.

Рассмотрим випадок багаторазового повторення однієї й тієї ж випробування чи випадкового експерименту. Результат кожного випробування вважатимемо які залежать від цього, який результат припало на попередніх випробуваннях. Як результатів чи елементарних фіналів кожного окремого випробування будемо розрізняти лише дві возможности:

1) поява деякого події А;

2) поява події  , (події, що є доповненням А)

Пусть ймовірність P(A) появи події А постійна і дорівнює p (0.p1). Можливість P( ) події   позначимо через q: P( ) = 1– p=q.

Примерами таких випробувань можуть быть:

1) підкидання монети: А – випадання герба;   – випадання цифры.

P(A) = P( ) = 0,5.

2) кидання гральною кістки: А – випадання кількості очок, рівного п'яти,   випадання будь-якого кількості очок крім пяти.

P(A) =1/6, P( ) =5/6.

3) вилучення наудачу з урни, що містить 7 білих хусток і 3 чорних кулі, одного кулі (з поверненням): А – вилучення білого кулі,   – вилучення чорного шара

P(A) = 0,7; P( ) = 0,3

Пусть вироблено n випробувань, які ми розглядати, як одне складне випадковий експеримент. Складемо таблицю з n клітин, розміщених у ряд, пронумеруємо клітини, і результати кожного випробування відзначатимемо так: тоді як 1-му випробуванні подія А сталося, то i-ю клітину ставимо цифру 1, якщо подія А сталося (відбулася подія  ), в i-ю клітину ставимо 0.

Если, наприклад, проведено 5 випробувань, й цю подію А відбулося лише у 2-му і 5-му випробуваннях, то результат можна записати такий послідовністю нулів і одиниць: 0; 1; 0; 0; 1.

Каждому можливого результату n випробувань відповідатиме послідовність n цифр 1 чи 0, які чергуються у порядку, у якому з'являються події A і   в n випробуваннях, например:

1; 1; 0; 1; 0; 1; 0; 0; ... 0; 1; 1; 0

14444442444443

n цифр

Всего таких послідовностей можна скласти   (це читач може довести сам).

Так як випробування незалежні, то ймовірність P кожної такої результату визначається шляхом перемножения ймовірностей подій A і   у випробуваннях. Приміром, для написаного вище результату найдем

P = p×p×q×p×q×p×q×q×...×q×p×p×q

Если в написаної нами послідовності одиниця зустрічається x раз (це що означає, що нуль зустрічається n–x раз), то ймовірність відповідного результату буде pnqn-x незалежно від цього, у порядку чергуються ці x одиниць і n–x нулей.

Все події, які у тому, що у n випробуваннях подія A сталося x раз, а подія   сталося n-x раз, є несовместными. Тож обчислення ймовірності об'єднання цих подій (чи суми цих подій), потрібно скласти ймовірності всіх подій, кожна з яких дорівнює pnqn-x  . Усього таких подій можна нарахувати стільки, скільки утворити різних послідовностей довжини n, містять x цифр " 1 " і n–x цифр " 0 " . Таких послідовностей виходить стільки, скількома способами можна розмістити x цифр " 1 " (чи n–x цифр " 0 " ) на n місцях, тобто кількість цих послідовностей одно 

Отсюда виходить формула Бернулли:

Pn(x) = 

По формулі Бернуллі розраховується можливість появи події A " x " разів у n повторних незалежнихвипробуваннях, де p – можливість появи події A щодо одного випробуванні, q - можливість появи події   щодо одного испытании.

Сформулированные умови проведення випробувань іноді називаються " схемою повторних незалежнихвипробувань " чи " схемою Бернуллі "

Число x появи події A в n повторних незалежних випробуваннях називається частотой.

Пример. З урни, що містить 2 білих хусток і 6 чорних куль, наудачу вибирається з поверненням 5 разів підряд один кулю. Підрахувати можливість, що 4 разу з'явиться білий шар.

В наведених вище позначеннях n=8; p=1/4; q=3/4; x=5. Потрібну ймовірність обчислюємо по формулі Бернулли:

По формулі Бернуллі можна визначити ймовірності всіх можливих частот: x=0,1,2,3,4,5.

Заметим, що тоді як цьому завданні вважати, що білих куль було 20000, а чорних 60000, то очевидно p і q залишаться незмінними. Однак у ситуації можна знехтувати поверненням витягнутого кулі після кожної вибірки (при дуже великих значеннях x) і слід вважати ймовірності всіх частот: x=0,1,2,... за такою формулою Бернулли.

Формула Бернуллі при заданих числах p і n дає змоги розраховувати ймовірність будь-який частоти x (0 £ x £ n).